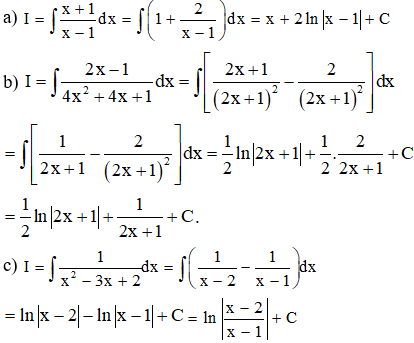100 công thức về nguyên hàm hữu tỉ, đẩy đủ, chi tiết nhất (2024) và cách giải các dạng toán
Công thức và cách giải các dạng toán về nguyên hàm hữu tỉ gồm phương pháp giải, ví dụ minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập các dạng toán về nguyên hàm hữu tỉ. Mời các bạn đón xem:
Công thức nguyên hàm hữu tỉ đầy đủ, chi tiết nhất
1. Lý thuyết
Bài toán tổng quát: Tính nguyên hàm với P(x) và Q(x) là các đa thức.
Phương pháp giải:
Nếu bậc của tử số P(x) lớn hơn hoặc bằng bậc của mẫu số Q(x) thì chia đa thức.
Nếu bậc của tử số P(x) nhỏ hơn bậc của mẫu số Q(x) thì xem xét mẫu số và khi đó:
- Nếu mẫu số phân tích được thành tích số, ta sẽ sử dụng đồng nhất thức để đưa về dạng tổng của các phân số.
Một số trường hợp đồng nhất thức thường gặp:
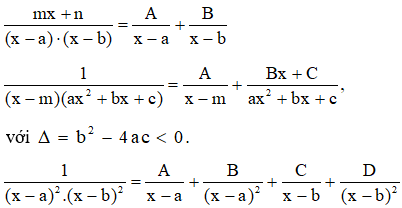
Nếu mẫu số không phân tích được thành tích số (biến đổi và đưa về dạng lượng giác).
2. Ví dụ minh họa
Ví dụ 1: Tính các nguyên hàm sau:
a)
b)
Lời giải
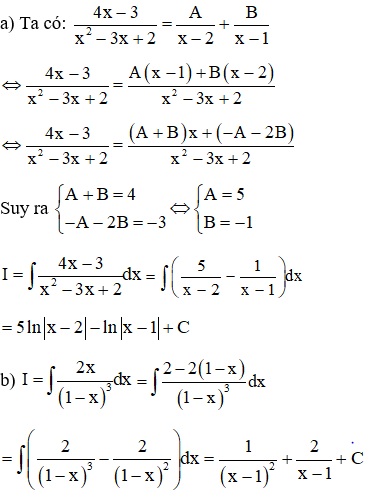
Ví dụ12: Tính các nguyên hàm sau:
a)
b)
c)
Lời giải
