100 bài tập về phương trình đường thẳng (2024 có đáp án) và cách giải các dạng toán

  

Các dạng toán về phương trình đường thẳng và cách giải 

I. LÝ THUYẾT

1. Vectơ chỉ phương của đường thẳng

- Vectơ $\overrightarrow{a}$ khác vectơ – không được gọi là vectơ chỉ phương của đường thẳng d nếu giá của vectơ $\overrightarrow{a}$ song song hoặc trùng với đường thẳng d.

- Nếu $\overrightarrow{a}$ là vectơ chỉ phương của đường thẳng d thì vectơ $k\overrightarrow{a}$ với $k\ne 0$ cũng là vectơ chỉ phương của đường thẳng d $\Rightarrow$ đường thẳng d có vô số vectơ chỉ phương và các vectơ chỉ phương này cùng phương.

- Một đường thẳng d trong không gian hoàn toàn xác định nếu biết một điểm A thuộc d và một vectơ chỉ phương $\overrightarrow{a}$ của nó.

2. Phương trình tham số – Phương trình chính tắc của đường thẳng

- Phương trình tham số của đường thẳng d đi qua điểm $M_0\left(x_0;y_0;z_0\right)$ và có vectơ chỉ phương $\overrightarrow{a}=\left(a_1;a_2;a_3\right)$ (với $a_1^2+a_2^2+a_3^2\ne 0$ ) là phương trình có dạng $d:\left\{\begin{array}{l}x=x_0+a_{1}t\\ y=y_0+a_{2}t\\ z=z_0+a_{3}t\end{array}\right.$ trong đó t là tham số.

- Nếu $a_1{a}_2{a}_3\ne 0$ thì ta có thể viết phương trình đường thẳng d dưới dạng chính tắc như sau: $d:\frac{x-x_0}{a_1}=\frac{y-y_0}{a_2}=\frac{z-z_0}{a_3}$

II. PHƯƠNG PHÁP GIẢI VÀ VÍ DỤ MINH HỌA

2.1 Dạng 1: Xác định vectơ chỉ phương (VTCP) của đường thẳng

Phương pháp giải:

Đường thẳng $\left(d\right):\left\{\begin{array}{l}x=x_0+at\\ y=y_0+bt\\ z=z_0+ct\end{array}\right.\left(t\in ℝ\right)$, hoặc $\left(d\right):\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}$ thì d đi qua $M\left(x_0;y_0;z_0\right)$ và có 1 VTCP $\overrightarrow{u}=\left(a;b;c\right)$.

$\overrightarrow{u}$ là 1 VTCP của d thì $k\overrightarrow{u}$ cũng là 1 VTCP của d.

Một số dạng thường gặp:

+) d qua hai điểm A, B thì $\overrightarrow{AB}$ là 1 VTCP của d.

+) $\left(d\right)\perp \left(P\right):$ Ax + By + Cz + D = 0 thì (A; B; C) là 1 VTCP của d.

+) $\left(d\right)\parallel \left(\Delta \right)$ mà $\left(\Delta \right)$ có VTCP $\overrightarrow{u}$ thì $\overrightarrow{u}$ cũng là 1 VTCP của d.

+) $\left(d\right)=\left(P\right)\cap \left(Q\right)$ thì $\overrightarrow{u}=\left[\overrightarrow{n_P},\overrightarrow{n_Q}\right]$ là 1 VTCP của d.

+) $\left(d\right)\perp \left(d_1\right)$ và $\left(d\right)\perp \left(d_2\right)$ thì $\overrightarrow{u}=\left[\overrightarrow{u_{d_1}},\overrightarrow{u_{d_2}}\right]$ là 1 VTCP của d.

+) $\left(d\right)\parallel \left(P\right)$ và $\left(d\right)\perp \left(\Delta \right)$ thì $\overrightarrow{u}=\left[\overrightarrow{n_P},\overrightarrow{u_{\Delta }}\right]$ là 1 VTCP của d.

Ví dụ 1: Trong không gian cho A (1; 1; 0) và B (0; 1; 2). Vectơ nào sau đây là một VTCP của đường thẳng AB?

A. $\overrightarrow{c}=\left(\text{1;2};\text{2}\right)$

B. $\overrightarrow{a}=\left(-1;0;2\right)$

C. $\overrightarrow{b}=\left(-\text{\hspace{0.17em}1;1;2}\right)$

D. $\overrightarrow{d}=\left(-1;0;-2\right)$

Hướng dẫn giải:

Một vectơ chỉ phương của đường thẳng AB là $\overrightarrow{AB}=\left(-1;0;2\right)$.

Chọn B.

Ví dụ 2: Cho (P): 3x – y + 2z – 7 = 0 và (Q): x + 3y – 2z + 3 = 0. Biết d là giao tuyến của (P) và (Q), một VTCP của d là:

A. $\overrightarrow{u}=\left(-2;4;5\right)$

B. $\overrightarrow{u}=\left(3;-1;2\right)$

C. $\overrightarrow{u}=\left(1;3;-2\right)$

D. $\overrightarrow{u}=\left(5;4;-2\right)$

Hướng dẫn giải:

(P) có vectơ pháp tuyến là $\overrightarrow{n_{\left(P\right)}}=\left(3;-1;2\right)$

(Q) có vectơ pháp tuyến là $\overrightarrow{n_{\left(Q\right)}}=\left(1;3;-2\right)$

Vì d là là giao tuyến của (P) và (Q) nên ta có :

$$\begin{gathered} \overrightarrow{u_d}=\left[\overrightarrow{n_P},\overrightarrow{n_Q}\right]=\left(-4;8;10\right) \\ =2\left(-2;4;5\right) \end{gathered}$$

Ta chọn VTCP là $\overrightarrow{u}=\left(-2;4;5\right)$

Chọn A.

2.2 Dạng 2: Viết phương trình đường thẳng đi qua 1 điểm và biết vectơ chỉ phương.

Phương pháp giải:

a) Loại 1: Viết phương trình đường thẳng $\Delta$ đi qua điểm $M\left(x_o;y_o;z_o\right)$ và có vectơ chỉ phương $\overrightarrow{u}=\left(u_1;u_2;u_3\right)$.

+) Phương trình tham số của đường thẳng $\Delta$ là: $\left\{\begin{array}{l}x=x_o+u_{1}t\\ y=y_o+u_{2}t\\ z=z_o+u_{3}t\end{array}\right..$ $\left(t\in ℝ\right)$

+) Phương trình chính tắc của đường thẳng $\Delta$ là: $\frac{x-x_0}{u_1}=\frac{y-y_o}{u_2}=\frac{z-z_o}{u_3}.$

b) Loại 2: Viết phương trình đường thẳng $\Delta$ đi qua hai điểm A, B.

+) Xác định vectơ chỉ phương của $\Delta$ là $\overrightarrow{u_{\Delta }}=\overrightarrow{AB}$.

+) Viết phương trình đường thẳng $\Delta$ qua điểm A và có VTCP là $\overrightarrow{AB}$

c) Loại 3: Viết phương trình đường thẳng $\Delta$ đi qua điểm M và song song với đường thẳng d.

+) Xác định vectơ chỉ phương của đường thẳng $\Delta$ là $\overrightarrow{u_{\Delta }}=\overrightarrow{u_d}$

+) Viết phương trình đường thẳng $\Delta$ qua điểm M và có VTCP là $\overrightarrow{u_{△}}$

Chú ý: Các trường hợp đặc biệt.

Nếu đường thẳng $\Delta$ song song với trục Ox thì có VTCP là $\overrightarrow{u_{\Delta }}=\overrightarrow{i}=\left(1;\text{ 0; 0}\right)$.

Nếu đường thẳng $\Delta$ song song với trục Oy thì có VTCP là $\overrightarrow{u_{\Delta }}=\overrightarrow{j}=\left(0;\text{ 1; 0}\right)$.

Nếu đường thẳng $\Delta$ song song với trục Oz thì có VTCP là $\overrightarrow{u_{\Delta }}=\overrightarrow{k}=\left(0;\text{ 0; 1}\right)$

d) Loại 4: Viết phương trình đường thẳng $\Delta$ đi qua điểm M và vuông góc với mặt phẳng $\left(\alpha \right)$.

+) Xác định vectơ chỉ phương của đường thẳng $\Delta$ là $\overrightarrow{u_{\Delta }}=\overrightarrow{n_{\alpha }}$

+) Viết phương trình đường thẳng $\Delta$ qua điểm M và có VTCP là $\overrightarrow{u_{△}}$.

Chú ý: Các trường hợp đặc biệt.

Nếu $\Delta$ vuông góc với mặt phẳng (Oxy) thì có VTCP là $\overrightarrow{u_{\Delta }}=\overrightarrow{k}=\left(0;\text{\hspace{0.17em}0;\hspace{0.17em}}1\right)$.

Nếu $\Delta$ vuông góc với mặt phẳng (Oxz) thì có VTCP là $\overrightarrow{u_{\Delta }}=\overrightarrow{j}=\left(0;1\text{;\hspace{0.17em}}0\right)$.

Nếu $\Delta$ vuông góc với mặt phẳng (Oyz) thì có VTCP là$\overrightarrow{u_{\Delta }}=\overrightarrow{i}=\left(1;\text{\hspace{0.17em}0;\hspace{0.17em}}0\right)$

Ví dụ 3: Viết phương trình đường thẳng đi qua điểm M (1; 2; -3) và có vectơ chỉ phương $\overrightarrow{u}=\left(3;-2;7\right)$.

A. $\left\{\begin{array}{l}x=1+3t\\ y=2-2t\\ z=-3+7t\end{array}\right..$

B. $\left\{\begin{array}{l}x=3+t\\ y=-2+2t\\ z=7-3t\end{array}\right..$

C. $\left\{\begin{array}{l}x=-3+7t\\ y=2-2t\\ z=1+3t\end{array}\right..$

D. $\left\{\begin{array}{l}x=1+3t\\ y=2+2t\\ z=3+7t\end{array}\right..$

Hướng dẫn giải:

Phương trình tham số của đường thẳng $\Delta$ là: $\left\{\begin{array}{l}x=1+3t\\ y=2-2t\\ z=-3+7t\end{array}\right..$

Chọn A.

Ví dụ 4: Trong không gian với hệ tọa độ Oxyz cho A (2; 3; -1), B (1; 2; 4), phương trình đường thẳng d đi qua hai điểm A, B là

A. $\left\{\begin{array}{l}x=2+t\\ y=3+2t\\ z=-1+4t\end{array}\right..$

B. $\left\{\begin{array}{l}x=1+2t\\ y=2+3t\\ z=4-t\end{array}\right..$

C. $\left\{\begin{array}{l}x=2-t\\ y=3-t\\ z=-1+5t\end{array}\right..$

D. $\left\{\begin{array}{l}x=-1+2t\\ y=-1+3t\\ z=5-t\end{array}\right..$

Hướng dẫn giải:

Đường thẳng d đi qua điểm A và nhận $\overrightarrow{AB}=\left(-1;-1;5\right)$ làm vectơ chỉ phương.

Nên phương trình đường thẳng d là: $d:\frac{x+2}{4}=\frac{y-5}{2}=\frac{z-2}{3}.$

Chọn C.

Ví dụ 5: Trong không gian với hệ tọa độ Oxyz hãy viết phương trình đường thẳng $∆$ đi qua điểm M (4; -2; 2) và song song với đường thẳng $\left\{\begin{array}{l}x=2-t\\ y=3-t\\ z=-1+5t\end{array}\right..$

A. $\left\{\begin{array}{l}x=4+4t\\ y=-2+2t\\ z=2+3t\end{array}\right..$

B. $\left\{\begin{array}{l}x=4+4t\\ y=2-2t\\ z=3+2t\end{array}\right..$

C. $\left\{\begin{array}{l}x=4-2t\\ y=-2+5t\\ z=2+2t\end{array}\right..$

D. $\left\{\begin{array}{l}x=2+4t\\ y=5-2t\\ z=2+2t\end{array}\right..$

Hướng dẫn giải:

Đường thẳng d có vectơ chỉ phương là $\overrightarrow{u_d}=\left(4;2;3\right).$

Vì đường thẳng $\Delta$ song song với đường thẳng d nên $\overrightarrow{u_{\Delta }}=\overrightarrow{u_d}=\left(4;2;3\right).$

Vì $\Delta$ đi qua điểm M nên ta có phương trình đường thẳng $\Delta$ là: $\left\{\begin{array}{l}x=4+4t\\ y=-2+2t\\ z=2+3t\end{array}\right..$

Chọn A.

Ví dụ 6: Trong không gian với hệ trục tọa độ Oxyz, viết phương trình đường thẳng $\Delta$ đi qua điểm A (-2; 4; 3) và vuông góc với mặt phẳng $\left(\alpha \right):$2x – 3y + 6z + 19 = 0.

A. $\frac{x-2}{2}=\frac{y+4}{-3}=\frac{z+3}{6}.$

B. $\frac{x+2}{2}=\frac{y+3}{4}=\frac{z-6}{3}.$

C. $\frac{x+2}{2}=\frac{y-4}{-3}=\frac{z-3}{6}.$

D. $\frac{x+2}{2}=\frac{y-3}{4}=\frac{z+6}{3}.$

Hướng dẫn giải:

Mặt phẳng $\left(\alpha \right)$ có vectơ pháp tuyến là $\overrightarrow{n_{\alpha }}=\left(2;-3;6\right)$.

Vì đường thẳng $\Delta$ vuông góc với mặt phẳng $\left(\alpha \right)$ nên $\overrightarrow{u_{\Delta }}=\overrightarrow{n_{\alpha }}=\left(2;-3;6\right)$.

Vì $\Delta$ đi qua điểm A (-2; 4; 3) nên phương trình đường thẳng$\Delta$ là: $\frac{x+2}{2}=\frac{y-4}{-3}=\frac{z-3}{6}.$

Chọn C.

2.3 Dạng 3: Viết phương trình đường thẳng đi qua 1 điểm, cắt d1 và thỏa mãn điều kiện khác

a) Loại 1: Viết phương trình đường thẳng $\Delta$ đi qua điểm $M\left(x_o;y_o;z_o\right)$, vuông góc và cắt đường thẳng d.

Phương pháp giải:

$\Delta$Gọi $H=\left(\Delta \right)\cap d.$

Tìm tọa độ điểm H từ điều kiện $\overrightarrow{MH}.\overrightarrow{u_d}=0$

là đường thẳng đi qua 2 điểm M và H.

Ví dụ 7: Trong không gian với hệ tọa độ Oxyz cho điểm M (2; 3; -1) và đường thẳng $\left(d\right):\frac{x}{2}=\frac{y}{4}=\frac{z-3}{1}.$ Gọi $\Delta$ là đưởng thẳng qua M, vuông góc và cắt d. Viết phương trình của $\Delta$

A. $\frac{x-2}{6}=\frac{y+3}{-5}=\frac{z+1}{32}$

B. $\frac{x+2}{6}=\frac{y+3}{5}=\frac{z-1}{32}$

C. $\frac{x-2}{6}=\frac{y-3}{5}=\frac{z+1}{-32}$

D. $\frac{x-2}{6}=\frac{y-3}{5}=\frac{z+1}{32}$

Hướng dẫn giải:

Đường thẳng d có vectơ chỉ phương là $\overrightarrow{u_d}=\left(2;4;1\right)$.

Gọi N là giao điểm của $\Delta$ và d. Vì $N\in d\Rightarrow$ N (2t; 4t; 3 + t).

Suy ra $\overrightarrow{MN}=\left(2t-2;4t-3;t+4\right)$

Vì $\Delta \perp d\Rightarrow \overrightarrow{MN}.\overrightarrow{u_d}=0$

$$\begin{gathered} \iff 2\left(2t-2\right)+4\left(4t-3\right)+t+4=0 \\ \iff t=\frac{4}{7}. \end{gathered}$$

Khi đó:

$$\begin{gathered} \overrightarrow{MN}=\left(-\frac{6}{7};-\frac{5}{7};\frac{32}{7}\right) \\ =-7\left(6;5;-32\right) \end{gathered}$$

Suy ra $\Delta$ có một vectơ chỉ phương là $\overrightarrow{u_{\Delta }}=\left(6;5;-32\right)$. Mà $\Delta$ đi qua M nên phương trình đường thẳng $\left(\Delta \right):\frac{x-2}{6}=\frac{y-3}{5}=\frac{z+1}{-32}$

Chọn C

b) Loại 2: Viết phương trình đường thẳng $\Delta$ đi qua điểm A vuông góc với đường thẳng $d_1$ và cắt đường thẳng $d_2.$

Phương pháp giải:

Gọi $B=\Delta \cap d_2$

Tìm tọa độ điểm B từ điều kiện $\overrightarrow{AB}.\overrightarrow{u_{d_1}}=0$

$\Delta$ là đường thẳng đi qua 2 điểm A, B.

Ví dụ 8: Trong không gian với hệ tọa độ Oxyz, cho điểm A (1; -1; 3) và hai đường thẳng: $d_1:\frac{x-4}{1}=\frac{y+2}{4}=\frac{z-1}{-2},$$d_2:\frac{x-2}{1}=\frac{y+1}{-1}=\frac{z-1}{1}.$

Viết phương trình đường thẳng d đi qua điểm A vuông góc với đường thẳng $d_1$và cắt đường thẳng $d_2.$

A. $\frac{x-1}{4}=\frac{y+1}{1}=\frac{z-3}{4}.$

B. $\frac{x-1}{2}=\frac{y+1}{1}=\frac{z-3}{3}$

C. $\frac{x-1}{2}=\frac{y+1}{-1}=\frac{z-3}{-1}$

D. $\frac{x-1}{-2}=\frac{y+1}{2}=\frac{z-3}{3}$

Hướng dẫn giải:

Gọi $M=d\cap d_2,$

$$\begin{gathered} {\text{\hspace{0.17em}\hspace{0.17em}d}}_2:\left\{\begin{array}{l}x=2+t\\ y=-1-t\\ z=1+t\end{array}\right. \\ \Rightarrow M\left(t+2,-t-1,t+1\right). \end{gathered}$$

Đường thẳng d nhận $\overrightarrow{AM}=\left(t+1;-t;t-2\right)$ là một VTCP.

Đường thẳng $d_1$ có vectơ chỉ phương là $\overrightarrow{u_1}=\left(1;4;-2\right).$

Ta có:

$$\begin{gathered} d\perp d_1\iff \overrightarrow{AM}.\overrightarrow{u}=0 \\ \iff \left(t+1\right)-4t-2\left(t-2\right)=0 \\ \iff t=1\Rightarrow \overrightarrow{AM}=\left(2;-1;-1\right). \end{gathered}$$

Đường thẳng d qua A (1; -1; 3) và nhận $\overrightarrow{AM}=\left(2;-1;-1\right)$ là một VTCP nên phương trình đường thẳng d là $d:\frac{x-1}{2}=\frac{y+1}{-1}=\frac{z-3}{-1}.$

Chọn C

Loại 3: Viết phương trình đường thẳng $∆$ đi qua điểm M và cắt hai đường thẳng $d_1$ và $d_2$ .

Phương pháp giải:

Gọi A, B lần lượt là giao điểm của d và $d_1$, d và $d_2.$

Đường thẳng d đi qua M nên A, B, M thẳng hàng

$\Rightarrow \overrightarrow{MA},\overrightarrow{MB}$ cùng phương $\overrightarrow{MA}=k\overrightarrow{MB}$. Từ đó tìm ra A và B.

Ví dụ 9: Trong không gian với hệ tọa độ Oxyz, cho điểm M (2; -1; -6) và hai đường thẳng $d_1:\frac{x-1}{2}=\frac{y-1}{-1}=\frac{z+1}{1}$ , $d_2:\frac{x+2}{3}=\frac{y+1}{1}=\frac{z-2}{2}$. Đường thẳng đi qua điểm M và cắt cả hai đường thẳng $d_1$, $d_2$tại hai điểm A, B. Độ dài đoạn thẳng AB bằng

A. $\sqrt{38}$.

B. $2\sqrt{10}$.

C. 8.

D. 12.

Hướng dẫn giải

Vì A thuộc $d_1:\frac{x-1}{2}=\frac{y-1}{-1}=\frac{z+1}{1}$ nên A (1 + 2t; 1 – t; -1 + t).

Vì B thuộc $d_2:\frac{x+2}{3}=\frac{y+1}{1}=\frac{z-2}{2}$ nên B (-2 + 3t’; -1 + t’; 2 + 2t’).

Suy ra $\overrightarrow{MA}=\left(2t-1;2-t;5+t\right)$,

$\overrightarrow{MB}=\left(-4+3t^{\text{'}};t^{\text{'}};8+2t^{\text{'}}\right)$.

Ta có A, B, M thẳng hàng khi và chỉ khi

$$\begin{gathered} \overrightarrow{MA}=k\overrightarrow{MB}\iff \left\{\begin{array}{l}2t-1=k\left(3t\text{'}-4\right)\\ 2-t=kt\text{'}\\ t+5=k\left(2t\text{'}+8\right)\end{array}\right. \\ \iff \left\{\begin{array}{l}t=1\\ t\text{'}=2\\ k=\frac{1}{2}\end{array}\right. \end{gathered}$$

Với t = 1, t’ = 2 ta được A (3; 0; 0), B (4; 1; 6), suy ra $AB=\sqrt{{\left(4-3\right)}^2+1^2+6^2}=\sqrt{38}$

Chọn A.

III. BÀI TẬP ÁP DỤNG

Câu 1: Trong không gian cho đường thẳng $d:\left\{\begin{array}{l}x=3+2t\\ y=-t\\ z=2\end{array}\right.$. Một vectơ chỉ phương của d là:

A. $\overrightarrow{u}=\left(2;-1;2\right)$

B. $\overrightarrow{u}=\left(3;0;2\right)$

C. $\overrightarrow{u}=\left(2;0;2\right)$

D. $\overrightarrow{u}=\left(2;-1;0\right)$

Câu 2: Trong không gian cho M (1; 2; 3). Gọi $M_1{M}_2$ lần lượt là hình chiếu của M lên Ox, Oy. Vectơ nào sau đây là VTCP của $M_1,M_2$ ?

A. $\overrightarrow{u}=\left(0;2;0\right)$

B. $\overrightarrow{u}=\left(1;2;0\right)$

C. $\overrightarrow{u}=\left(1;0;0\right)$

D. $\overrightarrow{u}=\left(-1;2;0\right)$

Câu 3: Trong không gian cho điểm A (0; 1; 2) và mặt phẳng (P): 2x – y + z – 4 = 0. Đường thẳng $\Delta$ qua A, cắt $d:\left\{\begin{array}{l}x=2+t\\ y=-4t\\ z=3\end{array}\right.$ và song song với (P) có một VTCP là:

A. $\overrightarrow{u}=\left(2;-1;1\right)$

B. $\overrightarrow{u}=\left(1;3;1\right)$

C. $\overrightarrow{u}=\left(1;1;-1\right)$

D. $\overrightarrow{u}=\left(2;2;1\right)$

Câu 4: Trong không gian cho đường thẳng d có phương trình $\frac{x-2}{-1}=\frac{y}{2}=\frac{z-1}{3}$. Một vectơ chỉ phương của d là

A. $\overrightarrow{u}=\left(0;2;1\right)$

B. $\overrightarrow{u}=\left(-2;0;-1\right)$

C. $\overrightarrow{u}=\left(-1;2;3\right)$

D. $\overrightarrow{u}=\left(1;2;3\right)$

Câu 5: Trong không gian với hệ tọa độ Oxyz cho A (3; -2; 0), B (1; 1; 4), C (-5; 3; 2), viết phương trình đường thẳng AM với M là trung điểm của đoạn thẳng BC

A. $\frac{x-3}{-6}=\frac{y+2}{2}=\frac{z}{-2}.$

B. $\frac{x-3}{-2}=\frac{y+2}{2}=\frac{z}{3}.$

C. $\frac{x+3}{-5}=\frac{y+2}{4}=\frac{z}{3}.$

D. $\frac{x-3}{-5}=\frac{y+2}{4}=\frac{z}{3}.$

Câu 6: Trong không gian với hệ tọa độ Oxyz hãy viết phương trình đường thẳng d đi qua điểm M (5; -1; 3) và vuông góc với mặt phẳng (Oxy).

A. $\left\{\begin{array}{l}x=5+t\\ y=-1+t\\ z=3\end{array}\right..$

B. $\left\{\begin{array}{l}x=5\\ y=-1\\ z=3+t\end{array}\right..$

C. $\left\{\begin{array}{l}x=5t\\ y=-t\\ z=1+3t\end{array}\right..$

D. $\left\{\begin{array}{l}x=1+5t\\ y=1-t\\ z=3t\end{array}\right..$

Câu 7: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1; 2; 4), B (-1; 5; 1), C (3; 2; 1) và mặt phẳng $\left(\alpha \right)$ - x + 4y – 2z + 6 = 0. Phương trình nào dưới đây là phương trình của đường thẳng đi qua trọng tâm của tam giác ABC và vuông góc với $\left(\alpha \right)$.

A. $\frac{x+1}{-1}=\frac{y+3}{4}=\frac{z+2}{-2}.$

B. $\frac{x+1}{1}=\frac{y-4}{3}=\frac{z+2}{2}.$

C. $\frac{x-1}{1}=\frac{y+4}{3}=\frac{z-2}{2}.$

D. $\frac{x-1}{-1}=\frac{y-3}{4}=\frac{z-2}{-2}.$

Câu 8: Trong không gian với hệ trục tọa độ Oxyz cho $d:\frac{x}{2}=\frac{y}{4}=\frac{z+3}{1},$điểm A (3; 2; 1). Viết phương trình đường thẳng $∆$ qua A, cắt đồng thời vuông góc với đường thẳng d.

A. $\left\{\begin{array}{l}x=3+3t\\ y=2-5t\\ z=1+4t\end{array}\right.$

B. $\left\{\begin{array}{l}x=1+3t\\ y=1-5t\\ z=1+4t\end{array}\right.$

C. $\left\{\begin{array}{l}x=1+9t\\ y=1-10t\\ z=1+22t\end{array}\right.$

D. $\left\{\begin{array}{l}x=3+9t\\ y=2-10t\\ z=1+22t\end{array}\right.$

Câu 9: Trong không gian với hệ tọa độ Oxyz, viết phương trình tham số của đường thẳng $\Delta$ đi qua điểm M (-1; 2; -3) và song song với đường thẳng$d:\frac{x}{2}=\frac{y+1}{2}=\frac{1-z}{3}.$

A. $\left\{\begin{array}{l}x=-1+2t\\ y=2+2t\\ z=-3+3t\end{array}\right..$

B. $\left\{\begin{array}{l}x=1+2t\\ y=2+2t\\ z=3+3t\end{array}\right..$

C. $\left\{\begin{array}{l}x=-1+2t\\ y=2-2t\\ z=-3-3t\end{array}\right..$

D. $\left\{\begin{array}{l}x=-1+2t\\ y=2+2t\\ z=-3-3t\end{array}\right..$

Câu 10: Viết phương trình chính tắc của đường thẳng $\Delta$ đi qua điểm A (3; -1; -4) cắt trục Oy và song song với mặt phẳng (P): 2x + y = 0.

A. $\frac{x-3}{-3}=\frac{y-1}{6}=\frac{z+4}{4}$

B. $\frac{x-3}{-3}=\frac{y+1}{6}=\frac{z+4}{-4}$

C. $\frac{x-3}{-3}=\frac{y+1}{6}=\frac{z+4}{4}$

D. $\frac{x+3}{3}=\frac{y-1}{6}=\frac{z+4}{4}$

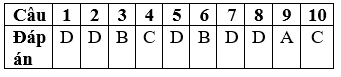
ĐÁP ÁN