100 bài tập về phương pháp giải các bài toán về các tập hợp số (2024 có đáp án) và cách giải các dạng toán
Cách giải các dạng toán về giải các bài toán về các tập hợp số và cách giải các dạng toán gồm phương pháp giải, ví dụ minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập các dạng toán về phương pháp giải các bài toán về các tập hợp số. Mời các bạn đón xem:
Phương pháp giải các bài toán về các tập hợp số hay nhất
A. Lý thuyết về tập hợp
1. Tập hợp
- Cho tập hợp A
+ Nếu a là phần tử thuộc tập A ta viết a ∈ A.
+ Nếu a là phần tử không thuộc tập a ta viết a ∉ A.
2. Một tập hợp xác định bởi
a) Viết tập hợp bằng cách liệt kê các phần tử của tập hợp
- Viết tất cả các phần tử của tập hợp vào giữa dấu{}, các phần tử cách nhau bằng dấu phẩy (,) hoặc chấm phẩy (;).
Ví dụ: A = {1,2,3,4,5,6}
b) Viết tập hợp bằng cách nếu tính chất đặc trưng của tập
- Chỉ ra tính chất đặc trưng cho các phần tử của tập đó
- Ta thường minh hoạ tập hợp bằng một đường cong khép kín gọi là biểu đồ ven
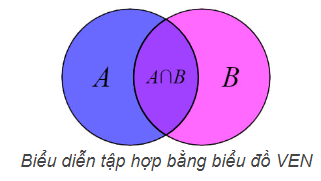
3. Tập hợp rỗng
- Là tập hợp không chứa phần tử nào, Ký hiệu là Ø
A ≠ Ø ⇔ ∃x: x ∈ A
4. Tập hợp con của một tập hợp
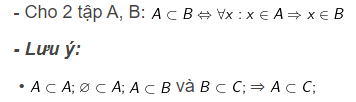
• Tập A có n phần tử thì A có 2n tập con.
5. Hai tập hợp bằng nhau
- Cho 2 tập A, B: A = B ⇔ A ⊂ B và B ⊂ A
6. Một số tập hợp số
a) Các tập hợp số

b) Mối quan hệ giữa các tập hợp số
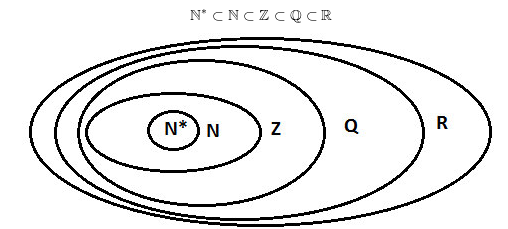
c) Các tập hợp con thường dùng của R
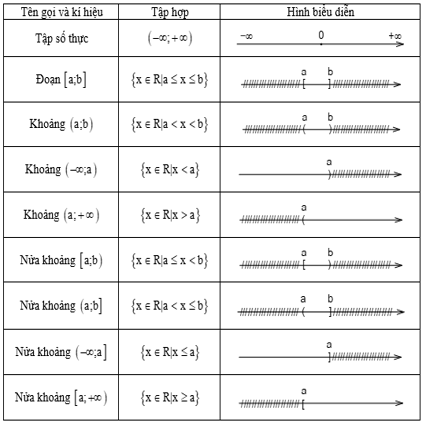
7. Các phép toán trên tập hợp

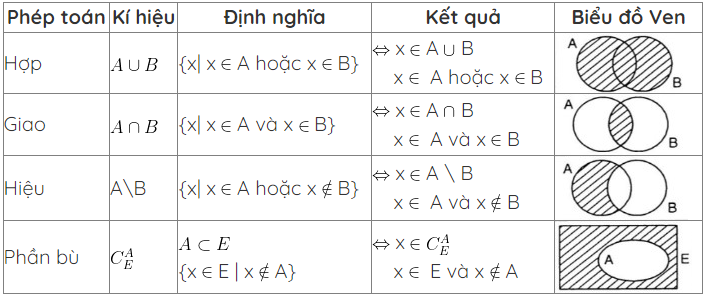
B. Các dạng bài toán về tập hợp
Dạng 1: Xác định tập hợp
* Phương pháp:
- Liệt kê các phần tử của tập hợp: A = {a1 , a2 , a3,...}
- Nêu tính đặc trưng của tập hợp: A = {x ∈ X| p(x)}
Ví dụ 1: Tìm tập hợp các nghiệm của phương trình: x(x-1)(x-2)(x2 -1) = 0
* Hướng dẫn:
- Liệt kê: A = {0, -1, 1, 2}
- A = {x ∈ Z | x(x-1)(x-2)(x2 -1) = 0} ⇔ A = {x ∈ Z | x(x-2)(x2 -1) = 0}
Ví dụ 2: Tìm tập hợp các số tự nhiên chẵn khác 0 và nhỏ hơn 10
* Hướng dẫn:
- Ta liệt kê các phần tử: A = {2,4,6,8} hoặc A = {x ∈ N* | x = BS(2) và x < 10}
Ví dụ 3: Viết tập hợp A = {2,3} bằng cách nêu ra tính chất đặc trưng của nó.
* Hướng dẫn:
- Ta có thể viết như sau:
A = {x ∈ N | 1 < x < 4}
A = {x ∈ N | 2 ≤ x ≤ 3}
A = {x ∈ N | (x-2)(x-3) = 0}
A = {x ∈ N | x2 - 5x + 6 = 0}
Dạng 2. Tập hợp con, Tập hợp bằng nhau
* Phương pháp: Áp dụng định nghĩa
+) A⊂B ⇔∀x∈A⇒x∈B?⊂? ⇔∀?∈?⇒?∈?
+) A ⊄ B ⇔ ∃x ∈ A ⇒ x ∉ B
+) A = B ⇔ A ⊂ B và B ⊂ A
+) A ≠ B ⇔ A ⊄ B hoặc B ⊄ A
Ví dụ 1: Cho các tập hợp: E = {-3; 4}, F = {-3; x2 } , G = {-3; x2 ; y}. Xác định x, y để E=F=G.
* Hướng dẫn:
- Để E = F thì x2 = 4 ⇒ x = 2 hoặc x = -2
- Để F = G thì y = - 3 hoặc y = x = 4
⇒ Để E = F = G thì x = ±2 và y = -3 hoặc y = 4;
Ví dụ 2: Cho A = {x | x(x-1)(x-2) = 0} Tìm các tập con của A và tập con đó có chứa phần tử 0
* Hướng dẫn:
- Liệt kê số phần tử của A = {0; 1; 2} vậy tập A có 23 = 8 tập con như sau:
{0}, {1}, {2}, {0;1}, {0;2}, {1;2} , {0;1;2} và Ø
⇒ Các tập có chứa phần tử 0 là: {0}, {0;1}, {0;2}, {0;1;2}
Ví dụ 3: Cho tập hợp,
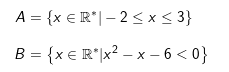
Xác định =, ≠ giữa A và B
* Hướng dẫn:
- Ta có: A = [-2;0) U (0;3] và B = (-2;0) U (0;3)
⇒ A ≠ B
Ví dụ 4: Cho 2 tập hợp A = {x ∈ Z| x3 - 2x2 - x + 2 = 0} và B = {x ∈ Z| x2 - 3x + 2 = 0} hãy đặt dấu ⊂ và ⊄ giữa A và B.
*Hướng dẫn:
- Ta liệt kê các phần tử tập A và B: A = {-1; 1; 2} , B = {1; 2}
⇒ B ⊂ A
Dạng 3. Các phép toán trên tập hợp, Giao, Hợp, Hiệu
* Phương pháp: Áp dụng định nghĩa
- Liệt kê A, B
- A ∩ B : Lấy các phần tử giống nhau của A và B
- A U B : Lấy tất cả các phần tử của A, của B và của A ∩ B (chung)
- A \ B: Lấy các phần tử của A và không phải của B
Ví dụ 1: Cho 2 tập hợp A = {x ∈ R | x2 - 4x + 3 ≤ 0} và A = {x ∈ R | x2 - 3x + 2 ≤ 0} tính A U B, A ∩ B, A \B và B \ A.
* Hướng dẫn:
- Liệt kê: A = {1;3} và B = {1;2} ta có:
A U B = {1;2;3} , A ∩ B = {1} , A\ B = {3} , B\ A = {2}
Ví dụ 2: Cho 2 tập hợp A = {x ∈ R | x2 - 4x + 3 = 0} và A = {x ∈ R | x2 - 3x + 2 = 0} tính A U B, A ∩ B, A \B và B \A.
* Hướng dẫn:
- Liệt kê: A = [1;3] và B = [1;2] ta có:
A U B = [1;3] , A ∩ B = [1;2] , A\ B = (2;3] , B\ A = ∅
Dạng 4. Giải toán bằng biểu đồ VEN
*Phương pháp: Áp dụng định nghĩa
Ví dụ 1: Mỗi học sinh của lớp 10A đều biết chơi cờ tướng hoặc cờ vua, biết rằng có 25 em biết chơi cờ tướng, 30 em biết chơi cờ vua, 15 em biết chơi cả hai. Hỏi lớp 10A có bao nhiêu em chỉ biết chơi cờ tướng? Bao nhiêu em chỉ biết chơi cờ vua? Sĩ số lớp là bao nhiêu?
* Hướng dẫn:
- Ta vẽ biểu đồ VEN như sau:
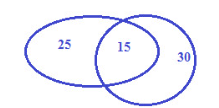
- Dựa vào sơ đồ Ven ta suy ra số học sinh chỉ biết chơi cờ tướng là 25 - 15 = 10.
- Số học sinh chỉ biết chơi cờ vua là: 30 - 15 = 15.
- Do đó ta có sĩ số học sinh của lớp 10A là: 10 + 15 + 15 = 40 học sinh.
Ví dụ 2: Lớp 10B có 45 học sinh, trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Sử, 66 em không thích môn nào, 55 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên là bao nhiêu?
*Hướng dẫn:
Ta vẽ biểu đồ VEN như sau:
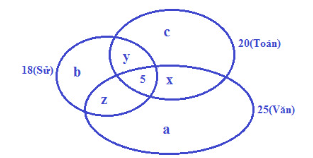
- Gọi: a, b, c theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán.
x là số học sịnh chỉ thích hai môn là Văn và Toán.
y là số học sịnh chỉ thích hai môn là Sử và Toán.
z là số học sịnh chỉ thích hai môn là Văn và Sử.
- Ta có số em thích ít nhất một môn là 45 - 6 = 39.
- Dựa vào sơ đồ Ven ta có hệ phương trình:
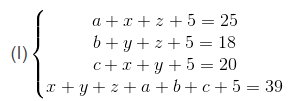
- Giải hệ phương trình (I) bằng cách cộng vế với vế 3 phương trình đầu ta có:
a + b + c + 2(x + y + z) + 15 = 63 kết hợp với phương trình cuối của hệ: x + y + z + a + b + c + 5 = 39 ta được:
a + b + c + 2(39 - 5 - a - b - c) + 15 = 63 ⇒ a + b + c = 20
⇒ Vậy chỉ có 20 em thích chỉ một môn trong ba môn trên.
C. Ví dụ minh họa
Ví dụ 1: Cho hai tập hợp A={x∈R|−5≤x<1}?=?∈ℝ|−5≤?<1;B={x∈R|−3<x≤3}?=?∈ℝ|−3<?≤3. Tìm A∩B?∩?
Hướng dẫn:
Ta có: A={x∈R|−5≤x<1}?=?∈ℝ|−5≤?<1 = [-5; 1) ( theo lý thuyết: [a;b)={x∈R| a≤x<b}?;?=?∈ℝ ?≤?<?)
B={x∈R|−3<x≤3}?=?∈ℝ|−3<?≤3= (-3; 3] ( theo lý thuyết: (a;b]={x∈R| a<x≤b}?;?=?∈ℝ ?<?≤? )
Ta biểu diễn tập hợp A và B trên trục số như sau:
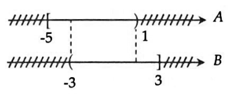
Vậy A∩B?∩? = (-3; 1).
Ví dụ 2: Xác định mỗi tập hợp sau và biểu diễn nó trên trục số.
a. (−3;3)∪(−1;0)(−3;3)∪(−1;0).
b. (−1;3)∪[0;5](−1;3)∪0;5.
c. (−2;2]∩[1;3)−2;2∩1;3.
Hướng dẫn:
Sử dụng trục số, đoạn (hoặc khoảng) nào không lấy, ta gạch bỏ, sử dụng tính chất giao và hợp của các tập hợp để tìm ra kết quả.
a. (−3;3)∪(−1;0)(−3;3)∪(−1;0) = (-3; 3).
![]()
b.(−1;3)∪[0;5](−1;3)∪0;5 = (-1; 5].
![]()
c. (−2;2]∩[1;3)−2;2∩1;3 = [1; 2]
![]()
Ví dụ 3: Cho các tập hợp :
A={x∈R|−3≤x≤2}?={?∈ℝ|−3≤?≤2}
B={x∈R|0<x≤7}?={?∈ℝ|0<?≤7}
C={x∈R|x<−1}?={?∈ℝ|?<−1}
D={x∈R|x≥5}?={?∈ℝ|?≥5}
Hãy dùng kí hiệu đoạn, khoảng, nửa khoảng để viết lại các tập hợp trên.
Hướng dẫn:
- Theo lý thuyết: [a;b]={x∈R| a≤x≤b}?;?=?∈ℝ ?≤?≤?
Vậy A={x∈R|−3≤x≤2}?={?∈ℝ|−3≤?≤2}= [-3; 2].
- Theo lý thuyết: (a;b]={x∈R| a<x≤b}?;?=?∈ℝ ?<?≤?.
Vậy B={x∈R|0<x≤7}?={?∈ℝ|0<?≤7} = (0; 7].
- Theo lý thuyết: (−∞;b)={x∈R| x<b}(−∞;?)=?∈ℝ ?<?.
Vậy C={x∈R|x<−1}?={?∈ℝ|?<−1} = (−∞;−1)(−∞;−1).
- Theo lý thuyết: [a;+∞)={x∈R| a≤x}?;+∞=?∈ℝ ?≤?.
Vậy D={x∈R|x≥5}?={?∈ℝ|?≥5} = [5;+∞)[5;+∞).
D. Bài tập tự luyện
Câu 1: Cho tập hợp A={x∈R|−3<x<1}?=?∈ℝ|−3<?<1. Tập A là tập nào sau đây?
A.{-3; 1}.
B. [-3; 1].
C. [-3; 1).
D. (-3; 1).
Hướng dẫn:
Chọn D.
Theo lý thuyết: (a;b)={x∈R| a<x<b}(?;?)=?∈ℝ ?<?<?
Vậy A={x∈R|−3<x<1}?=?∈ℝ|−3<?<1= (-3; 1).
Câu 2: Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp (1; 4]?
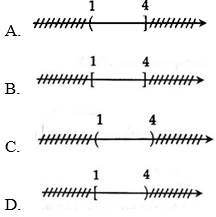
Hướng dẫn:
Chọn A. Vì (1; 4] gồm các số thực x mà 1<x≤41<?≤4
Đáp án B sai vì [1; 4] gồm các số thực x mà 1≤x≤41≤?≤4.
Đáp án C sai vì (1; 4) gồm các số thực x mà 1 < x < 4.
Đáp án B sai vì [1; 4) gồm các số thực x mà 1≤x<41≤?<4.
Câu 3: Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp A={x∈R|4≤x≤9}?=?∈ℝ4≤?≤9:
A. A = [4; 9].
B. A = (4; 9].
C. A = [4; 9).
D. A = (4; 9)
Hướng dẫn:
Chọn A.
Theo lý thuyết: [a;b]={x∈R| a≤x≤b}?;?=?∈ℝ ?≤?≤?. Suy ra A={x∈R|4≤x≤9}?=?∈ℝ4≤?≤9= [4; 9] .
Câu 4: Cho hai tập hợp A = [-2; 7); B = (1; 9]. Tìm A∪B?∪?.
A. (1; 7).
B. [-2; 9].
C. [-2; 1).
D. (7; 9].
Hướng dẫn:
Chọn B.
Ta biểu diễn tập hợp A và B trên trục số như sau:
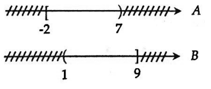
Vậy A∪B?∪? = [−2;7)∪(1;9]=[−2;9]−2;7∪1;9=−2;9
Câu 5: Cho tập hợp X={x|x∈R,1≤|x|≤3}?=?|?∈ℝ,1≤?≤3 thì X được biểu diễn là hình nào sau đây?
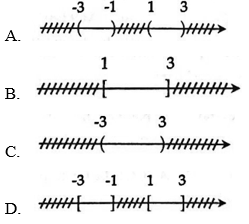
Hướng dẫn:
Chọn D.
Giải bất phương trình:
1≤|x|≤3⇔{|x|≥1|x|≤3⇔⎧⎪⎨⎪⎩[x≥1x≤−1−3≤x≤3⇔⎡⎢ ⎢ ⎢ ⎢⎣{x≥1−3≤x≤3{x≤−1−3≤x≤3⇔[1≤x≤3−3≤x≤−1⇔x∈[−3;−1]∪[1;3]1≤?≤3⇔?≥1?≤3⇔?≥1?≤−1−3≤?≤3⇔?≥1−3≤?≤3?≤−1−3≤?≤3⇔1≤?≤3−3≤?≤−1⇔?∈−3;−1∪1;3
Vậy đáp án D thỏa mãn x∈[−3;−1]∪[1;3]?∈−3;−1∪1;3.
Câu 6: Cho hai tập hợp A = (1; 5]; B = (2; 7]. Tập hợp A \ B là:
A. (1; 2].
B. (2; 5).
C. (-1; 7].
D. (-1; 2).
Hướng dẫn:
Chọn A.
Ta biểu diễn tập hợp A và B trên trục số:
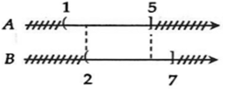
Vậy A \ B = {x∈R?∈ℝ| x∈A?∈? và x∉B?∉?}⇒x∈(1;2]⇒?∈1;2
Câu 7: Cho các số thực a, b, c, d và a < b < c < d. Khẳng định nào sau đây là đúng?
A. (a;c)∩(b;d)=(b;c)?;?∩?;?=?;?
B. (a;c)∩(b;d)=(b;c]?;?∩?;?=?;?
C. (a;c)∩(b;d)=[b;c)?;?∩?;?=?;?
D. (a;c)∪(b;d)=[b;c]?;?∪?;?=?;?
Hướng dẫn:
Chọn A.
Ta biểu diễn (a; c); (b; d) trên trục số sau đó dựa vào tính chất giao của hai tập hợp để tìm ra đáp án:
![]()
Vậy (a;c)∩(b;d)=(b;c)?;?∩?;?=?;?.
Câu 8: Cho tập hợp A = [m; m+2]; B = [-1; 2]. Tìm điều kiện của m để A⊂B?⊂?.
A.m≤−1?≤−1 hoặc m≥0?≥0.
B. −1≤m≤0−1≤?≤0
C. 1≤m≤21≤?≤2
D. m < 1 hoặc m > 2.
Hướng dẫn:
Chọn B.
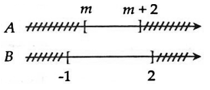
Điều kiện để A⊂B?⊂? là: −1≤m<m+2≤2−1≤?<?+2≤2.
⇔{m≥−1m+2≤2⇔{m≥−1m≤0⇔−1≤m≤0⇔?≥−1?+2≤2⇔?≥−1?≤0⇔−1≤?≤0
Câu 9: Cho hai tập hợp A = [-2; 3]; B = (m; m+6). Điều kiện để A⊂B?⊂? là:
A. −3≤m≤−2−3≤?≤−2
B. −3<m<−2−3<?<−2
C. m<−3?<−3
D.m≥−2?≥−2
Hướng dẫn:
Chọn B.
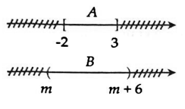
Điều kiện để A⊂B?⊂? là :
m<−2<3<m+6⇔{m<−2m+6>3⇔{m<−2m>−3⇔−3<m<−2?<−2<3<?+6⇔?<−2?+6>3⇔?<−2?>−3⇔−3<?<−2
Câu 10: Cho hai tập hợp X = (0; 3] và Y = (a; 4). Tìm tất cả các giá trị của a≤4?≤4 để X∩Y≠∅?∩?≠∅.
A. [a<3a≥4?<3?≥4.
B. a < 3.
C. a < 0.
D. a > 3.
Hướng dẫn:
Chọn B.
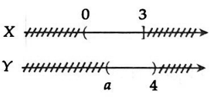
Xét:
X∩Y=∅⇒{a≥3a≤4⇔3≤a≤4?∩?=∅⇒?≥3?≤4⇔3≤?≤4
⇒X∩Y≠∅⇔[a<3a>4.⇒?∩?≠∅⇔?<3?>4.Mà theo đề bài,a≤4?≤4 nên suy ra a < 3.
Vậy với a < 3 thì X∩Y≠∅?∩?≠∅.