100 bài tập về tích phân hàm phân thức hữu tỉ và lượng giác (2024 có đáp án) và cách giải các dạng toán

Tích phân hàm phân thức hữu tỉ và lượng giác và cách giải 

A. TÍCH PHÂN CỦA HÀM SỐ PHÂN THỨC HỮU TỈ

Phương pháp giải chung: Phân tích hàm phân thức hữu tỉ để đưa về các tích phân cơ bản.

1. Một số công thức cần thiết.

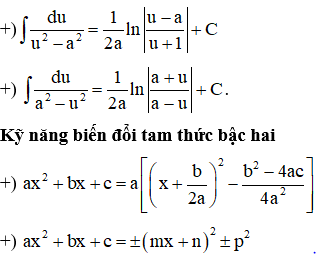
2. Các dạng toán thường gặp, công thức giải nhanh và ví dụ minh hoạ.

2.1. Dạng 1: Tích phân dạng $I_1=\underset{\alpha }{\overset{\beta }{\int }}\frac{dx}{a{x}^2+bx+c}$.

Phương pháp giải:

Biến đổi :

$$\begin{gathered} I_1=\underset{\alpha }{\overset{\beta }{\int }}\frac{dx}{a{x}^2+bx+c}=\underset{\alpha }{\overset{\beta }{\int }}\frac{dx}{{\left(mx+n\right)}^2-p^2} \\ ={\left.\left[\frac{1}{2mp}\ln \left|\frac{mx+n-p}{mx+n+p}\right|\right]\right|}_{\alpha }^{\beta } \end{gathered}$$

Ví dụ 1. Cho $I=\underset{0}{\overset{1}{\int }}\frac{dx}{4x^2+8x+1}=\frac{\ln \left(\frac{a+b\sqrt{3}}{13}\right)}{c\sqrt{3}}$, với $a,b,c\in ℝ;c\ne 0$. Đặt S = a + b + c, lúc này S có giá trị bằng

A. $S=20+37\sqrt{3}$

B. $S=37+24\sqrt{3}$

C. $S=57$

D. $S=61$

Lời giải

Áp dụng bài toán tổng quát trên ta có:

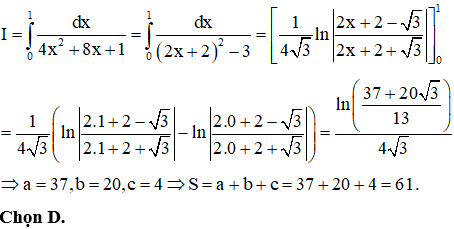
2.2. Dạng 2: Tính tích phân $I_2=\underset{\alpha }{\overset{\beta }{\int }}\frac{mx+n}{a{x}^2+bx+c}dx$.

Phương pháp giải

Cách 1:

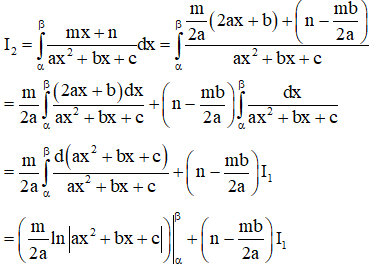
Cách 2: Phương pháp hệ số bất định (Sử dụng khi mẫu có nghiệm)

* Nếu mẫu số có nghiệm kép $x=x_0$ tức là $a{x}^2+bx+c=a{\left(x-x_0\right)}^2$ ta giả sử:

$\frac{mx+n}{a{x}^2+bx+c}=\frac{A}{x-x_0}+\frac{B}{{\left(x-x_0\right)}^2}$

Quy đồng vế phải và đồng nhất hệ số hai vế để tìm A; B.

Sau khi tìm được A; B thì ta có $I_2={\left[A.\ln \left|x-x_0\right|-\frac{B}{x-x_0}\right]}_{\alpha }^{\beta }$.

* Nếu mẫu số có 2 nghiệm phân biệt $x_1;x_2$: $a{x}^2+bx+c=a\left(x-x_1\right)\left(x-x_2\right)$ thì ta giả sử:

$\frac{mx+n}{a{x}^2+bx+c}=\frac{A}{x-x_1}+\frac{B}{x-x_2}$

Quy đồng và đồng nhất hệ số để tìm A; B.

Sau khi tìm được A; B ta có $I_2={\left.\left[A\ln \left|x-x_1\right|+B\ln \left|x-x_2\right|\right]\right|}_{\alpha }^{\beta }$.

Ví dụ 2. Cho $I=\underset{-2}{\overset{0}{\int }}\frac{2x-9}{x^2-3x+2}dx=a\ln 3+b\ln 2$, $a;b\in \mathbb{Z}$ thì a + 2b có giá trị bằng:

A. ‒35

B. ‒2

C. 2

D. 3

Chọn D.

Lời giải

Cách 1: Ta có:

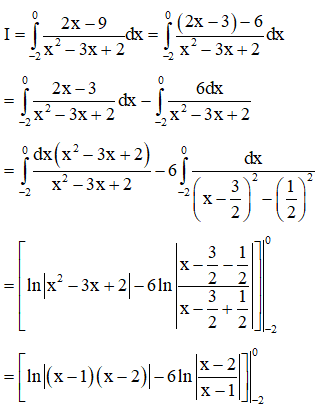
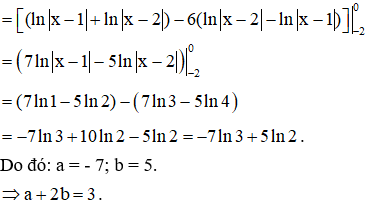
Cách 2: Ta thấy .

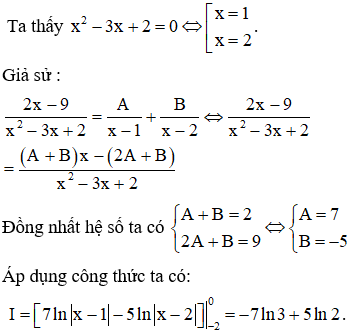
Cách 3: Sử dụng máy tính cầm tay.

Trong bài toán này ta có thể sử dụng chức năng TABLE để giải quyết, tuy nhiên cách làm này chỉ mang tính chất “mò” (tức dự đoán khoảng của a; b).

Ta thấy:

$I=a.\ln 3+b.\ln 2\Rightarrow a=\frac{I-b.\ln 2}{\ln 3}$

1. Lúc này ta nhập biểu thức tích phân vào máy tính và gán giá trị này cho biến A.

2. Tiếp tục sử dụng MODE 7 TABLE để chạy biến giá trị của b từ đó tìm ra bảng giá trị tương ứng của a.

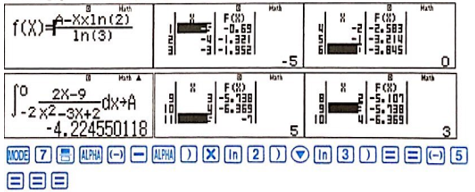
Ta thấy chỉ có trường hợp $X=5;F\left(X\right)=-7$ là thỏa mãn 2 số nguyên, do đó ta kết luận $a=-7;b=5\Rightarrow a+2b=3$.

3. Bài tập tự luyện.

Câu 1. Tích phân $I=\underset{0}{\overset{1}{\int }}\frac{1}{x^2-x-2}dx$ có giá trị bằng

A. $\frac{2\ln 2}{3}$

B. $-\frac{2\ln 2}{3}$

C. $-2\ln 2$

D. $2\ln 2$

Câu 2. Với 0 < a < 1, giá trị của tích phân sau $\underset{0}{\overset{a}{\int }}\frac{dx}{x^2-3x+2}dx$ là:

A. $\ln \left|\frac{a-2}{2a-1}\right|$

B. $\ln \left|\frac{a-2}{a-1}\right|$

C. $\ln \left|\frac{a-2}{2\left(a-1\right)}\right|$

D. $\ln \left|\frac{a-2}{2a+1}\right|$.

Câu 3. Giá trị của tích phân $I=\underset{-1}{\overset{0}{\int }}\frac{x^3-3x^2+2}{x^2+x-2}dx$ gần nhất với gái trị nào sau đây?

A. $-\frac{\ln 2}{2}$

B. $\ln 2-1$

C. $\frac{3}{2}-\ln 4$

D. $-\frac{\ln 3}{3}$

Câu 4. Tích phân $I=\underset{1}{\overset{2}{\int }}\frac{ax+1}{x^2+3x+2}dx=\frac{3}{5}\ln \frac{4}{3}+\frac{3}{5}\ln \frac{2}{3}$. Giá trị của a là:

A. $a=\frac{1}{5}$

B. $a=\frac{2}{5}$

C. $a=\frac{3}{5}$

D. $a=\frac{4}{5}$

Câu 5. Cho $I=\underset{0}{\overset{1}{\int }}\frac{1}{3+2x-x^2}dx=\left(a-b\right)\ln 2+b\ln 3$. Giá trị a + b là:

A. $\frac{1}{4}$

B. $\frac{1}{2}$

C. $\frac{1}{6}$

D. $\frac{1}{3}$

Câu 6. Tính: $I=\underset{0}{\overset{1}{\int }}\frac{dx}{x^2+4x+3}$

A. $I=\ln \frac{3}{2}$

B. $I=\frac{1}{3}\ln \frac{3}{2}$

C. $I=-\frac{1}{2}\ln \frac{3}{2}$

D. $I=\frac{1}{2}\ln \frac{3}{2}$

Câu 7. Tính: $I=\underset{0}{\overset{1}{\int }}\frac{dx}{x^2-5x+6}$

A. I = 1

B. $I=\ln \frac{3}{4}$

C. I = ln2

D. I = -ln2

Câu 8. Tính $I=\underset{0}{\overset{1}{\int }}\frac{(2x^2+5x-2)dx}{x{}_3+2x^2-4x-8}$

A. $I=\frac{1}{6}+\ln 12$

B. $I=\frac{1}{6}+\ln \frac{3}{4}$

C. $I=\frac{1}{6}-\ln 3+2\ln 2$

D. $I=\frac{1}{6}-\ln 3-2\ln 2$

Câu 9. Tính: $K=\underset{0}{\overset{2}{\int }}\frac{(x-1)}{x^2+4x+3}dx$

A. K = 1

B. K = 2

C. K = -2

D. Đáp án khác.

Câu 10. Biết $\underset{0}{\overset{1}{\int }}\frac{x^3+3x}{x^2+3x+2}dx=a+b\ln 2+c\ln 3$ với a, b, c là các số hữu tỉ, tính $S=2a+b^2+c^2.$

A. $S=515$

B. $S=164$

C. $S=436$

D. $S=-9$.

Câu 11. Biết $I=\underset{0}{\overset{4}{\int }}\frac{\sqrt{2x+1}dx}{2x+3\sqrt{2x+1}+3}=a+b\ln 2+c\ln \frac{5}{3}$ với a, b, c nguyên.

Tính T = a + b + c.

A. T = 4.

B. T = 2.

C. T = 1.

D. T = 3.

Câu 12. Tính tích phân $I=\underset{0}{\overset{1}{\int }}\frac{(x+4)dx}{x^2+3x+2}$

A. $5\ln 2-3\ln 2$

B. $5\ln 2+2\ln 3$

C. $5\ln 2-2\ln 3$

D. $2\ln 5-2\ln 3$

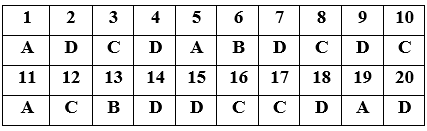
Đáp án

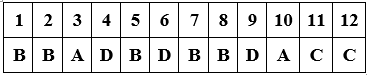
B. TÍCH PHÂN CỦA HÀM SỐ LƯỢNG GIÁC

1. Một số công thức và kĩ năng biến đổi.

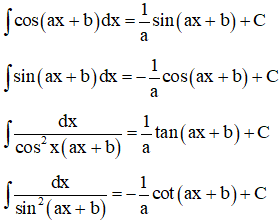
2. Các dạng toán hay gặp và cách giải.

2.1. Dạng 1: Tính tích phân: $I_1=\underset{a_1}{\overset{b_1}{\int }}{\left(\sin x\right)}^{n}dx;I_2=\underset{a_2}{\overset{b_2}{\int }}{\left(\cos x\right)}^{n}dx$

1. Nếu n chẵn thì ta sử dụng công thức hạ bậc.

2. Nếu n = 3 thì ta sử dụng công thức hạ bậc hoặc biến đổi theo trường hợp 3.

3. Nếu $n\ge 3$ và n lẻ $\left(n=2p+1\right)$ thì ta thực hiện biến đổi.

$$\begin{gathered} I_1=\underset{a_1}{\overset{b_1}{\int }}{\left(\sin x\right)}^{n}dx=\underset{a_1}{\overset{b_1}{\int }}{\left(\sin x\right)}^{2p+1}dx \\ =\underset{a_1}{\overset{b_1}{\int }}{\left(\sin x\right)}^{2p}.\sin xdx=-\underset{a_1}{\overset{b_1}{\int }}{\left(1-{\cos }^{2}x\right)}^{p}d\left(\cos x\right) \end{gathered}$$

Sử dụng công thức khai triển nhị thức Newton để khai triển ${\left(1-{\cos }^{2}x\right)}^p$

Từ đây ta giải quyết được bài toán.

$$\begin{gathered} I_2=\underset{a_2}{\overset{b_2}{\int }}{\left(\cos x\right)}^{n}dx=\underset{a_2}{\overset{b_2}{\int }}{\left(\cos x\right)}^{2p+1}dx \\ =\underset{a_2}{\overset{b_2}{\int }}{\left(\cos x\right)}^{2p}.\cos x.dx \\ =\underset{a_2}{\overset{b_2}{\int }}{\left(1-{\sin }^{2}x\right)}^{p}d\left(\sin x\right) \end{gathered}$$

Sử dụng công thức khai triển nhị thức Newton để khai triển ${\left(1-{\sin }^{2}x\right)}^p$.

Từ đây ta giải quyết dc bài toán.

2.2. Dạng 2: Tính tích phân $I=\underset{a}{\overset{b}{\int }}{\sin }^{m}x.{\cos }^{n}xdx$.

Trường hợp 1: m; n là các số nguyên

- Nếu m chẵn, n chẵn thì sử dụng công thức hạ bậc, biến đổi tích thành tổng.

- Nếu m chẵn, n lẻ $\left(n=2p+1\right)$ thì biến đổi

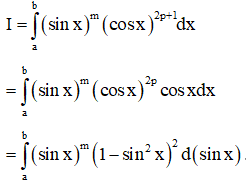
Sử dụng công thức khai triển nhị thức Newton để khai triển và giải quyết bài toán.

- Nếu m lẻ $\left(m=2p+1\right)$, n chẵn thì ta biến đổi

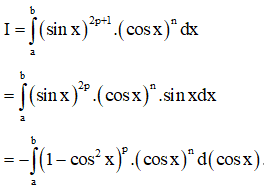
Sử dụng công thức khai triển nhị thức Newton để khai triển và giải quyết bài toán.

- Nếu m lẻ, n lẻ thì sử dụng biến đổi 2 hoặc 3 cho số mũ lẻ bé hơn.

Trường hợp 2: m; n là các số hữu tỉ:

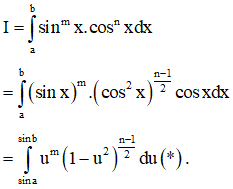
2.3. Dạng 3: Tính tích phân $I_1=\underset{a_1}{\overset{b_1}{\int }}{\left(\tan x\right)}^{n}dx;I_2=\underset{a_2}{\overset{b_2}{\int }}{\left(\cot x\right)}^{n}dx\left(n\in {\mathbb{N}}^{*}\right)$

Sử dụng các công thức sau:

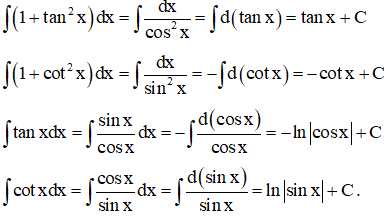
3. Đổi biến số với hàm lượng giác.

Khi nguyên hàm, tích phân của các hàm số mà biểu thức của nó có chứa các dạng $\sqrt{x^2+a^2},\sqrt{x^2-a^2},\sqrt{a^2-x^2}$, thì ta có cách biến đổi lượng giác như sau:

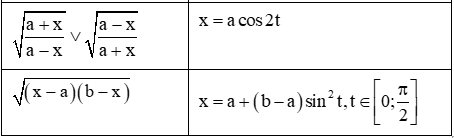
4. Ví dụ minh hoạ.

Ví dụ 1. Cho $I=\underset{0}{\overset{\frac{\pi }{10}}{\int }}{\cos }^{4}3xdx$. Đẳng thức nào sau đây đúng?

A. $I={\left.\left[\frac{3}{8}x+\frac{1}{12}\sin 6x+\frac{1}{96}\sin 12x\right]\right|}_0^{\frac{\pi }{10}}$

B. $I={\left.\left[\frac{1}{12}\sin 6x+\frac{1}{96}\sin 12x\right]\right|}_0^{\frac{\pi }{10}}$

C. $I={\left.\left[-\frac{3}{8}x+\frac{1}{12}\sin 6x+\frac{1}{96}\sin 12x\right]\right|}_0^{\frac{\pi }{10}}$

D. $I={\left.\left[\frac{3}{8}x-\frac{1}{96}\sin 12x\right]\right|}_0^{\frac{\pi }{10}}$

Lời giải

Ta có

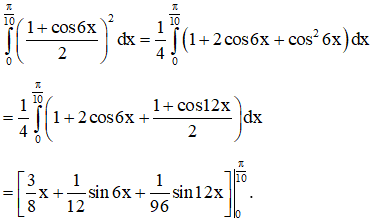
Từ đây ta giải quyết được bài toán.

Chọn A.

Ví dụ 2. Cho:

A. $S=3$

B. $S=-\frac{74}{105}$

C. $S=-\frac{5}{4}$

D. $S=\frac{1}{9}$

Lời giải

Ta có :

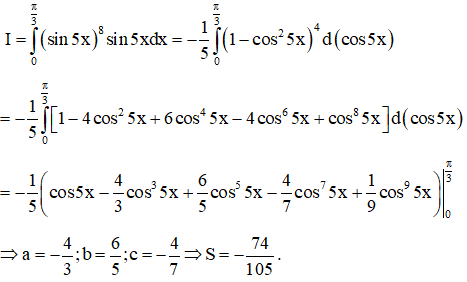
Chọn B.

Ví dụ 3. Cho $I=\underset{0}{\overset{\frac{\pi }{3}}{\int }}{\left(\sin 2x\right)}^7.{\left(\cos 2x\right)}^{100}dx$. Đẳng thức nào sau đây là đúng?

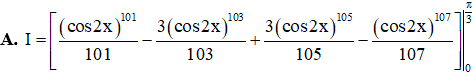
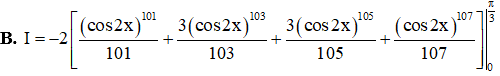
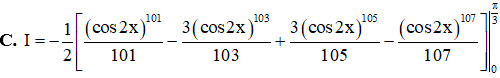
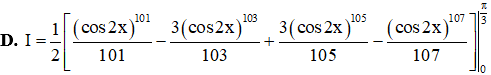
Lời giải

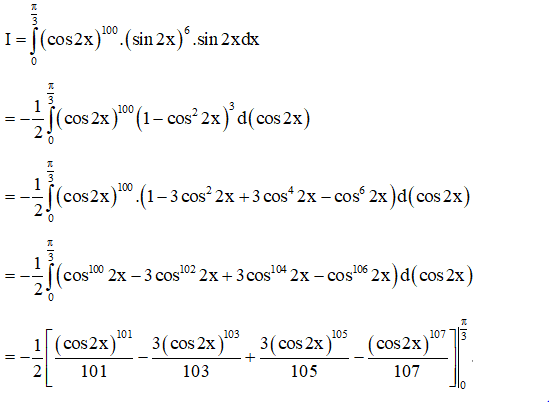
Chọn C.

5. Bài tập tự luyện.

Câu 1. Trong các hàm số dưới đây, hàm số nào có tích phân trên đoạn $[0;\pi ]$ đạt giá trị bằng 0?

A. $f\left(x\right)=\cos 3x$

B. $f\left(x\right)=\sin 3x$

C. $f\left(x\right)=\cos \left(\frac{x}{4}+\frac{\pi }{2}\right)$

D. $f\left(x\right)=\sin \left(\frac{x}{4}+\frac{\pi }{2}\right)$.

Câu 2. Giả sử hàm số f liên tục trên đoạn [0; 2] thỏa mãn $\underset{0}{\overset{2}{\int }}f\left(x\right)dx=6$. Giá trị của tích phân $\underset{0}{\overset{\pi /2}{\int }}f\left(2\sin x\right)\cos xdx$ là

A. -6.

B. 6.

C. -3.

D. 3.

Câu 3. Tích phân $I=\underset{\frac{\pi }{3}}{\overset{\frac{\pi }{2}}{\int }}\frac{dx}{\sin x}$ có giá trị bằng

A. $\frac{1}{2}\ln \frac{1}{3}$

B. $2\ln 3$

C. $\frac{1}{2}\ln 3$

D. $2\ln \frac{1}{3}$.

Câu 4. Xét tích phân $I=\underset{0}{\overset{\pi /3}{\int }}\frac{\sin 2x}{1+\cos x}dx$. Thực hiện phép đổi biến t = cosx, ta có thể đưa I về dạng nào sau đây

A. $I=-\underset{0}{\overset{\pi /4}{\int }}\frac{2t}{1+t}dt$

B. $I=\underset{0}{\overset{\pi /4}{\int }}\frac{2t}{1+t}dt$

C. $I=-\underset{\frac{1}{2}}{\overset{1}{\int }}\frac{2t}{1+t}dt$

D. $I=\underset{\frac{1}{2}}{\overset{1}{\int }}\frac{2t}{1+t}dt$.

Câu 5. Giá trị của tích phân $\underset{\frac{\pi }{3}}{\overset{\frac{2\pi }{3}}{\int }}\cos (3x-\frac{2\pi }{3})dx$ là:

A. $-\frac{\sqrt{3}}{3}$

B. $-\frac{\sqrt{2}}{3}$

C. $-\frac{2\sqrt{3}}{3}$

D. $-\frac{2\sqrt{2}}{3}$.

Câu 6. Giá trị của tích phân $\text{I}=\underset{0}{\overset{\frac{\pi }{2}}{\int }}{\cos }^{2}x\cos 2xdx$ là:

A. $\frac{\pi }{6}$

B. $\frac{\pi }{8}$

C. $\frac{\pi }{4}$

D. $\frac{\pi }{2}$

Câu 7. Giá trị tích phân $J=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left({\sin }^{4}x+1\right)\cos xdx$ là:

A. $\frac{2}{5}$

B. $\frac{3}{5}$

C. $\frac{4}{5}$

D. $\frac{6}{5}$.

Câu 8. Giá trị tích phân $I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{\sin x}{1+3\cos x}dx$ là:

A. $\frac{2}{3}\ln 2$.

B. $\frac{2}{3}\ln 4$

C. $\frac{1}{3}\ln 4$

D. $\frac{1}{3}\ln 2$.

Câu 9. Tích phân $I=\underset{0}{\overset{\frac{\pi }{3}}{\int }}{\sin }^{2}x\tan xdx$ có giá trị bằng:

A . $\ln 3-\frac{3}{5}$

B. $\ln 2-2$

C. $\ln 2-\frac{3}{4}$

D. $\ln 2-\frac{3}{8}$.

Câu 10. Cho tích phân $I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\sqrt{1+3\cos x}.\sin xdx$. Đặt $u=\sqrt{3\cos x+1}$.Khi đó I bằng:

A. $\frac{2}{3}\underset{1}{\overset{3}{\int }}{u}^{2}du$

B. $\frac{2}{3}\underset{0}{\overset{2}{\int }}{u}^{2}du$

C. ${\left.\frac{2}{9}{u}^3\right|}_1^2$

D. $\underset{1}{\overset{3}{\int }}{u}^{2}du$

Câu 11. Giá trị của tích phân $I=\underset{0}{\overset{\frac{1}{2}}{\int }}\frac{1}{\sqrt{1-x^2}}dx$ là?

A. $\frac{\pi }{6}$

B. $\frac{\pi }{4}$.

C. $\frac{\pi }{3}$

D. $\frac{\pi }{2}$.

Câu 12. Giá trị của tích phân $I=\underset{0}{\overset{1}{\int }}\frac{dx}{1+x^2}$ là?

A. $I=\frac{\pi }{2}$

B. $I=\frac{3\pi }{4}$

C. $I=\frac{\pi }{4}$

D. $I=\frac{5\pi }{4}$

Câu 13. Giá trị của tích phân $I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}({\sin }^{4}x+{\cos }^{4}x)({\sin }^{6}x+{\cos }^{6}x)dx$ là?

A. $I=\frac{32}{128}\pi$

B. $I=\frac{33}{128}\pi$

C. $I=\frac{31}{128}\pi$

D. $I=\frac{30}{128}\pi$

Câu 14. Giá trị của tích phân $I=\underset{0}{\overset{\pi }{\int }}\frac{xdx}{\sin x+1}$ là?

A. $I=\frac{\pi }{4}$

B. $I=\frac{\pi }{2}$

C. $I=\frac{\pi }{3}$

D. $I=\pi$

Câu 15. Giá trị của tích phân $\underset{0}{\overset{\frac{\pi }{2}}{\int }}{\cos }^{11}xdx$ là?

A. $\frac{250}{693}$

B. $\frac{254}{693}$

C. $\frac{252}{693}$

D. $\frac{256}{693}$

Câu 16. Giá trị của tích phân $\underset{0}{\overset{\frac{\pi }{2}}{\int }}{\sin }^{10}xdx$ là?

A. $\frac{67\pi }{512}$

B. $\frac{61\pi }{512}$

C. $\frac{63\pi }{512}$

D. $\frac{65\pi }{512}$

Câu 17. Với $n\in \mathbb{N},n\ge 1$, tích phân $I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}{\left(1-\cos x\right)}^n\sin xdx$ có giá trị bằng?

A. $\frac{1}{2n}$

B. $\frac{1}{n-1}$

C. $\frac{1}{n+1}$

D. $\frac{1}{n}$

Câu 18. Giá trị của tích phân $I=\underset{\frac{\pi }{6}}{\overset{\frac{\pi }{2}}{\int }}\frac{1}{{\sin }^{2}x}\ln \left(\sin x\right)dx$ là?

A. $-\sqrt{3}\ln 2+\sqrt{3}+\frac{\pi }{3}$

B. $\sqrt{3}\ln 2+\sqrt{3}-\frac{\pi }{3}$

C. $-\sqrt{3}\ln 2-\sqrt{3}-\frac{\pi }{3}$

D. $-\sqrt{3}\ln 2+\sqrt{3}-\frac{\pi }{3}$

Câu 19. Giá trị của tích phân $I=\underset{0}{\overset{\frac{\pi }{3}}{\int }}\frac{\cos x}{\sqrt{2+\cos 2x}}dx$ là?

A. $\frac{\pi }{4\sqrt{2}}$

B. $\frac{\pi }{2\sqrt{2}}$

C. $\frac{4\pi }{\sqrt{2}}$

D. $\frac{-\pi }{\sqrt{2}}$

Câu 20. Cho $\underset{0}{\overset{1}{\int }}f\left(x\right)dx=2018$. Tính tích phân $\underset{0}{\overset{\frac{\pi }{4}}{\int }}f\left(\sin 2x\right)\cos 2xdx$?

A. 2018.

B. -1009.

C. -2018.

D. 1009.

Đáp án