100 bài tập về thể tích khối chóp (2024 có đáp án) và cách giải các dạng toán
Cách giải các dạng toán về thể tích khối chóp gồm phương pháp giải, ví dụ minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập các dạng toán về thể tích khối chóp. Mời các bạn đón xem:
Nội dung bài viết
Xem thêm »
Thể tích khối chóp và cách giải bài tập
I. LÝ THUYẾT
1. Hình chóp
Là hình có 1 đỉnh và 1 đáy là đa giác lồi. Các mặt còn lại gọi là mặt bên và luôn là tam giác.
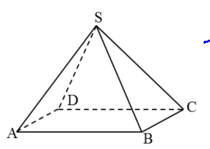
+) Mặt đáy: ABCD.
+) Các mặt bên: (SAB), (SBC), (SCD), (SDA).
+) Các cạnh bên: SA, SB, SC, SD.
+) Đỉnh hình chóp: S.
2. Thể tích khối chóp
Thể tích khối chóp bằng một phần ba tích của diện tích mặt đáy và chiều cao của khối chóp đó.
Công thức:
V=13B.h
B: Diện tích mặt đáy.
h: Chiều cao của khối chóp.
II. PHƯƠNG PHÁP
Dạng 1: Khối chóp có một cạnh bên vuông góc với đáy
Từ giả thiết của đề bài, ta xác định được đường cao h là cạnh bên vuông góc với đáy. Do vậy ở dạng toán này ta chỉ cần nắm vững các công thức tính độ dài và góc trong hình phẳng để áp dụng tìm cạnh, đoạn của đáy và đường cao. Từ đó ta tính được diện tích đáy và đường cao.
+ TH1: Khối chóp có đáy là tam giác ABC có SA vuông góc với đáy.
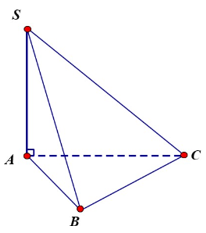
V=13.SABC.SA.
+ TH2: Khối chóp có đáy là hình vuông, hình chữ nhật, hình thoi, hình thang, hình bình hành, … và SA vuông góc với đáy.
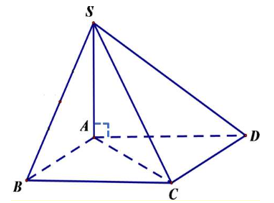
V=13.SABCD.SA
Ví dụ 1: Cho khối chóp S. ABC có SA vuông góc với đáy, SA = 4, AB = 6, BC = 10 và CA = 8. Tính thể tích khối chóp S. ABC.
A. V = 40.
B. V = 192.
C. V = 32.
D. V = 24.
Hướng dẫn giải
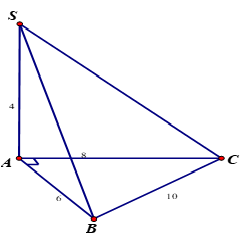
Ta có AB2+AC2=62+82=102=BC2 suy ra tam giác ABC vuông tại A (theo định lý Py – ta – go đảo), do đó diện tích tam giác ABC là: S=12AB.AC=12.6.8=24
Vì SA vuông góc với đáy nên SA là đường cao của hình chóp.
Do đó h = SA = 4.
Vậy VSABC=13.SA.SABC=13.4.24=32 (đvtt).
Chọn C.
Dạng 2: Khối chóp có một mặt bên vuông góc với đáy
Xét hình chóp S. ABCD có mặt bên (SAD)⊥(ABCD)
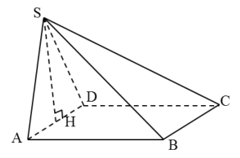
Đường cao của hình chóp là đường cao của tam giác SAD. Chứng minh:
{(SAD)⊥(ABCD)(SAD)∩(ABCD)=ADSH⊂(SAD)SH⊥AD⇒SH⊥(ABCD)
Đặc biệt nếu tam giác SAD cân hoặc đều thì đường cao cũng là đường trung tuyến và đường phân giác.
⇒VS.ABCD=13.SABCD.SH
Ví dụ 2: Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh 2a, tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Thể tích khối chóp S. ABC là
A. V=a32
B. V=a3
C. V=3a32
D. V=3a3
Hướng dẫn giải
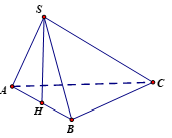
Chọn B.

Dạng 3: Thể tích khối chóp đều.
Xét hình chóp tứ giác đều S. ABCD
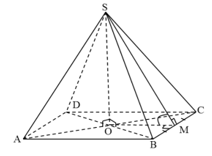
+) Các mặt bên là các tam giác cân tại S.
+) Đáy ABCD là hình vuông.
+) Đường cao là SO với O là tâm của đáy.
+) Các mặt bên tạo với đáy các góc bằng nhau và bằng góc SMO (với M là trung điểm của BC).
+) Các cạnh bên tạo với đáy các góc bằng nhau:
^SAO=^SBO=^SCO=^SDO⇒VS.ABCD=13SABCD.SO
Chú ý:
a) Với hình chóp tam giác đều ta làm tương tự.
b) Với tứ diện đều:
Xét tứ diện đều ABCD:
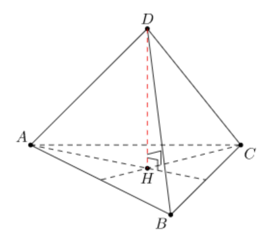
DH là đường cao của tứ diện đều (Với H là trọng tâm tam giác ABC).
Suy ra thể tích của khối tứ diện đều ABCD là V=13.SABC.DH .
Ví dụ 3: Cho hình chóp tứ giác đều S. ABCD có cạnh đáy bằng a và cạnh bên tạo với mặt phẳng đáy một góc 600 . Tính thể tích của khối chóp S. ABCD.
A. V=a3√62
B. V=a3√63
C. V=a3√32
D. V=a3√66
Hướng dẫn giải
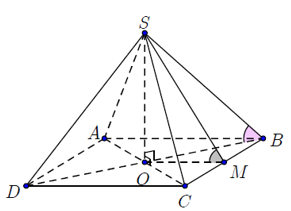
Gọi O là tâm hình vuông ABCD, suy ra SO⊥(ABCD) .
Hình chóp tứ giác đều có đáy là hình vuông nên ta có : SABCD=a2 và BD=a√2 . Suy ra BO=BD2=a√22
Ta có OB là hình chiếu vuông góc của SB lên mặt phẳng (ABCD) nên góc giữa cạnh bên SB với đáy là góc SBO bằng 600 .
Suy ra chiều cao SO :
SO=OB.tan^SBO=a√22.tan600=a√62
Vậy :
VS.ABCD=13.SABCD.SO=13.a2.a√62=a3√66
Chọn D.
Ví dụ 4: Cho khối chóp tam giác đều S. ABC có cạnh đáy bằng a và cạnh bên bằng 2a. Tính thể tích V của khối chóp S. ABC.
A. V=√13a312
B. V=√11a312
C. V=√11a36
D. V=√11a34
Hướng dẫn giải
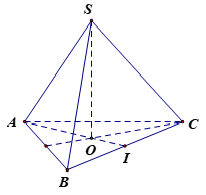
Gọi O là trọng tâm tam giác ABC suy ra SO⊥(ABCD) .
Do đáy là tam giác đều nên gọi I là trung điểm cạnh BC, khi đó AI là đường cao của tam giác đáy.
Ta có: BC = a nên BI=a2 .
Áp dụng định lý Pytago trong tam giác vuông ABI ta có:
AI=√AB2−BI2=√a2−a24=a√32
Ta có: AO=23AI=2a√33.2=a√33 (Do O là trọng tâm tam giác ABC).
Áp dụng định lý Pytago trong tam giác SOA vuông tại O ta có
SO=√SA2−AO2=√4a2−a23=√11a√3
Vậy thể tích khối chóp S. ABC là:
V=13SABC.SO=13.12a.a√32.√11a√3=√11a312
Chọn B.
Dạng 4: Cạnh bên hoặc mặt bên tạo với đáy một góc α và một số bài toán khác
Các giả thiết của bài toán này khá đa dạng, tuy nhiên cách giải của các bài toán này nằm ở 2 bước sau:
+) Bước 1: Xác định được góc trên hình vẽ.
+) Bước 2: Áp dụng các hệ thức lượng trong tam giác để tính các yếu tố cạnh liên quan tới chiều cao và diện tích đáy.
Ví dụ 5: Cho hình chóp tam giác S. ABC có SA = 2a. SA tạo với mặt phẳng (ABC) góc 30°. Tam giác ABC vuông cân tại B, G là trọng tâm tam giác ABC. Hai mặt phẳng (SGB), (SGC) cùng vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp S. ABC theo a.
A.
B.
C.
D.
Hướng dẫn giải
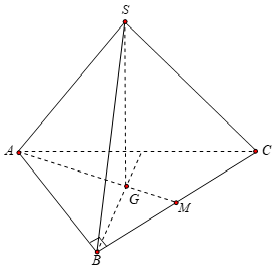

Xét tam giác ABM vuông tại B, có: (định lý Py – ta – go)
Vì tam giác ABC vuông cân tại B nên:
Chọn B.
III. BÀI TẬP ÁP DỤNG
Câu 1: Cho hình chóp tam giác S. ABC có đáy ABC là tam giác vuông tại A, AB = a, AC = 2a, cạnh bên SA vuông góc với mặt đáy và SA = a. Tính thể tích V của khối chóp S. ABC.
A.
B.
C.
D.
Câu 2: Cho hình chóp tam giác S. ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt đáy và SA = a. Tính thể tích V của khối chóp S. ABC.
A.
B.
C.
D.
Câu 3: Cho hình chóp tứ giác S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy và . Tính thể tích V của khối chóp S. ABCD.
A.
B.
C.
D.
Câu 4: Cho hình chóp S. ABC có đáy ABC là tam giác vuông cân tại A, BC = 2a. Mặt bên SBC là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S. ABC.
A.
B.
C.
D.
Câu 5: Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh , mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S. ABCD là
A.
B.
C.
D.
Câu 6: Cho hình chóp S. ABCD có đáy là hình chữ nhật với AB = 2a, AD = a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, SC tạo với đáy một góc . Thể tích khối chóp S. ABCD là
A.
B.
C.
D.
Câu 7: Cho hình chóp tam giác đều S. ABC có cạnh đáy bằng a và chiều cao của hình chóp là . Tính theo a thể tích khối chóp S. ABC.
A.
B.
C.
D.
Câu 8: Tính thể tích của chóp tam giác đều có tất cả các cạnh đều bằng a.
A.
B.
C.
D.
Câu 9: Cho (H) là khối chóp tứ giác đều có tất cả các cạnh bằng a. Thể tích của (H) bằng
A.
B.
C.
D.
Câu 10: Cho hình chóp S. ABC có diện tích đáy là 5, chiều cao có số đo gấp 3 lần diện tích đáy. Thể tích của khối chóp đó là
A.
B. 125
C.
D. 25.
Câu 11: Cho khối chóp S. ABCD có đáy là hình chữ nhật có chiều rộng 2a, chiều dài 3a. Chiều cao của khối chóp là 4a. Thể tích khối chóp S. ABCD tính theo a là
A.
B.
C.
D. .
BẢNG ĐÁP ÁN