100 bài tập về nguyên hàm của hàm số phân thức hữu tỉ (2024 có đáp án) và cách giải các dạng toán

Nguyên hàm của hàm số phân thức hữu tỉ và cách giải 

A. LÝ THUYẾT VÀ PHƯƠNG PHÁP GIẢI.

Cho hàm số y = f(x) có dạng $f\left(x\right)=\frac{P\left(x\right)}{Q\left(x\right)}$ trong đó P và Q là các đa thức, và P không chia hết cho Q.

- Hàm f(x) được gọi là hàm phân thức hữu tỉ thực sự nếu bậc của P < bậc của Q.

- Trong các bài toán tìm nguyên hàm và tích phân của hàm phân thức hữu tỉ, nếu f(x) chưa phải là hàm phân thức hữu tỉ thực sự thì ta thực hiện chia tử thức cho mẫu thức để được

$$\begin{gathered} f\left(x\right)=\frac{P\left(x\right)}{Q\left(x\right)}=S\left(x\right)+\frac{R\left(x\right)}{Q\left(x\right)} \\ =S\left(x\right)+h\left(x\right) \end{gathered}$$

Khi đó, $h\left(x\right)$ sẽ là hàm phân thức hữu tỉ thực sự.

Ta có: Một phân thức thực sự luôn phân tích được thành tổng các phân thức đơn giản hơn. Đó là các biểu thức có dạng $\frac{1}{x-a};\frac{1}{{\left(x-a\right)}^k};\frac{ax+b}{x^2+px+q};\frac{ax+b}{{\left(x^2+px+q\right)}^k}$ là các hàm số có thể tìm nguyên hàm một cách dễ dàng. Để tách được phân thức ta dùng phương pháp hệ số bất định.

1. Trường hợp phương trình Q(x) = 0 có nghiệm thực và các nghiệm đều là nghiệm đơn.

$Q\left(x\right)=\left(a_{1}x+b_1\right)\left(a_{2}x+b_2\right)\mathrm{...}\left(a_k{x}_k+b_k\right)$

(Số nhân tử chính bằng bậc của đa thức $Q\left(x\right)$).

Trong trường hợp này, g(x) có thể biểu diễn dưới dạng:

$$\begin{gathered} g\left(x\right)=\frac{R\left(x\right)}{Q\left(x\right)} \\ =\frac{A_1}{a_{1}x+b_1}+\frac{A_2}{a_{2}x+b_2}+\mathrm{...}+\frac{A_k}{a_{k}x+b_k} \end{gathered}$$

Sau khi biểu diễn được g(x) về dạng này, bài toán trở thành bài toán cơ bản.

Ví dụ về cách phân tích:

$$\begin{gathered} \frac{4x-3}{x^2-3x+2}=\frac{4x-3}{\left(x-2\right)\left(x-1\right)} \\ =\frac{A}{x-1}+\frac{B}{x-2}=\frac{Ax-2A+Bx-B}{\left(x-1\right)\left(x-2\right)} \end{gathered}$$

Khi đó $\left(A+B\right)x-2A-B=4x-3$, đồng nhất hệ số thì ta được

$\left\{\begin{array}{l}A+B=4\\ 2A+B=3\end{array}\right.\iff \left\{\begin{array}{l}A=-1\\ B=5\end{array}\right.$

Khi đó ta được:

$$\begin{gathered} \frac{4x-3}{x^2-3x+2}=\frac{4x-3}{\left(x-2\right)\left(x-1\right)} \\ =\frac{-1}{x-1}+\frac{5}{x-2} \end{gathered}$$

2. Trường hợp Q(x) = 0 có nghiệm thực là nghiệm bội.

- Nếu phương trình $Q\left(x\right)=0$ có các nghiệm thực $a_1;a_2;\mathrm{...};a_n$ trong đó $a_1$ là nghiệm bội k thì ta phân tích $g\left(x\right)=\frac{R\left(x\right)}{Q\left(x\right)}$ về dạng

Ví dụ về cách phân tích:

$$\begin{gathered} g\left(x\right)=\frac{A_1}{\left(x-a_1\right)}+\frac{A_2}{{\left(x-a_1\right)}^2} \\ +\mathrm{...}+\frac{A_k}{{\left(x-a_1\right)}^k}+\frac{B_1}{x-a_2}+\frac{B_2}{x-a_3} \\ +\mathrm{...}+\frac{B_{n+1}}{x-a_n} \end{gathered}$$

Từ đây, đồng nhất hệ số ta có

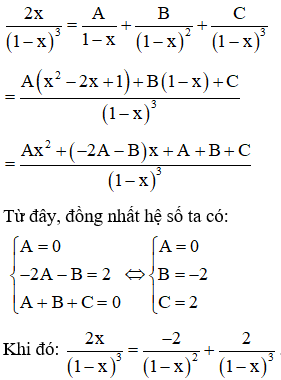
TỔNG QUÁT: Việc tính nguyên hàm của hàm phân thức hữu tỉ thực sự sau khi phân tích được đưa về các dạng nguyên hàm sau:

1. $\int \frac{A}{x-a}dx=A.\ln \left|x-a\right|+C,k\ne 1$

2. $\int \frac{A}{{\left(x-a\right)}^k}dx=-\frac{A}{k-1}.\frac{1}{{\left(x-a\right)}^{k-1}}+C$

3. Mở rộng: Nguyên hàm hàm phân thức chứa căn ở mẫu thức

Dạng 1: $I=\underset{}{\overset{}{\int }}\frac{dx}{\sqrt{a{x}^2+bx+c}}$

Phương pháp chung

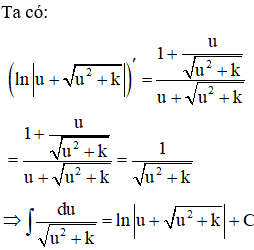
Dạng 2: $I=\underset{}{\overset{}{\int }}\frac{\left(mx+n\right)dx}{\sqrt{a{x}^2+bx+c}}$

Phương pháp chung

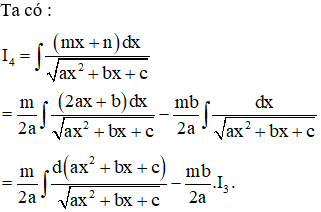
Dạng 3 : $I=\underset{}{\overset{}{\int }}\frac{dx}{\left(px+q\right)\sqrt{a{x}^2+bx+c}}$

Phương pháp chung

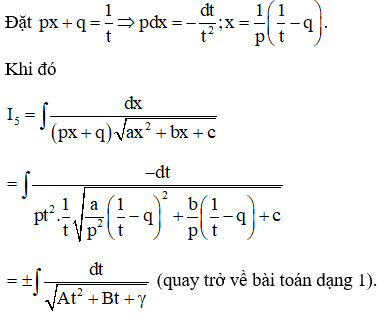
4. Nguyên hàm của một số nguyên hàm liên quan trong dạng bài này.

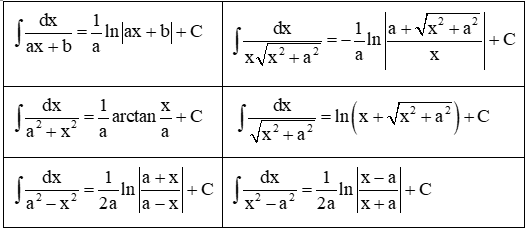
B. VÍ DỤ MINH HOẠ.

Ví dụ 1. Nguyên hàm $\int \frac{2x^3-6x^2+4x+1}{x^2-3x+2}dx$ là:

A. $x^2+\ln \left|\frac{x-1}{x-2}\right|+C$

B. $\frac{1}{2}{x}^2+\ln \left|\frac{x-2}{x-1}\right|+C$

C. $\frac{1}{2}{x}^2+\ln \left|\frac{x-1}{x-2}\right|+C$

D. $x^2+\ln \left|\frac{x-2}{x-1}\right|+C$ .

Lời giải

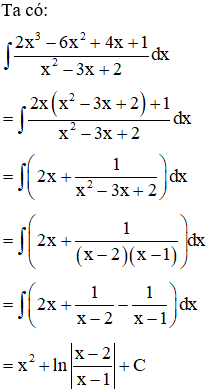
Đáp án đúng là D.

Ví dụ 2. Nguyên hàm $\int \frac{1}{x^2-7x+6}dx$ là:

A. $\frac{1}{5}\ln \left|\frac{x-1}{x-6}\right|+C$

B. $\frac{1}{5}\ln \left|\frac{x-6}{x-1}\right|+C$ .

C. $\frac{1}{5}\ln \left|x^2-7x+6\right|+C$ .

D. $-\frac{1}{5}\ln \left|x^2-7x+6\right|+C$ .

Lời giải

Ta có:

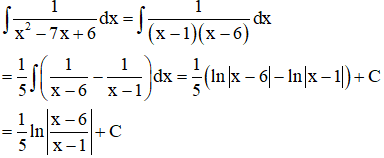
Đáp án đúng là B.

C. BÀI TẬP TỰ LUYỆN.

Câu 1. Tìm nguyên hàm của hàm số $f\left(x\right)=\frac{x^3+3x^2+3x-7}{{(x+1)}^2}$ với F(0) = 8 là:

A. $\frac{x^2}{2}+x+\frac{8}{x+1}$

B. $\frac{x^2}{2}+x-\frac{8}{x+1}$

C. $\frac{x^2}{2}-x+\frac{8}{x+1}$

D. Một kết quả khác

Câu 2. $\int \frac{1}{\left(x+1\right)\left(x+2\right)}dx$ bằng:

A. $\ln \left|x+1\right|+\ln \left|x+2\right|+C$

B. $\ln \left|\frac{x+1}{x+2}\right|+C$

C. $\ln \left|x+1\right|+C$

D. $\ln \left|x+2\right|+C$

Câu 3. $\int \frac{x+1}{x^2-3x+2}dx$ bằng:

A. $3\ln \left|x-2\right|-2\ln \left|x-1\right|+C$

B. $3\ln \left|x-2\right|+2\ln \left|x-1\right|+C$

C. $2\ln \left|x-2\right|-3\ln \left|x-1\right|+C$

D. $2\ln \left|x-2\right|+3\ln \left|x-1\right|+C$

Câu 4. $\int \frac{1}{x^2-4x-5}dx$ bằng:

A. $\ln \left|\frac{x-5}{x+1}\right|+C$

B. $6\ln \left|\frac{x-5}{x+1}\right|+C$

C. $\frac{1}{6}\ln \left|\frac{x-5}{x+1}\right|+C$

D. $-\frac{1}{6}\ln \left|\frac{x-5}{x+1}\right|+C$

Câu 5. Tìm nguyên hàm: $\underset{}{\overset{}{\int }}\frac{1}{x(x-3)}dx$

A. $\frac{1}{3}\ln \left|\frac{x}{x-3}\right|+C$

B. $\frac{1}{3}\ln \left|\frac{x+3}{x}\right|+C$

C. $\frac{1}{3}\ln \left|\frac{x}{x+3}\right|+C$

D. $\frac{1}{3}\ln \left|\frac{x-3}{x}\right|+C$

Câu 6. $\int \frac{1}{x^2+6x+9}dx$ bằng:

A. $-\frac{1}{x+3}+C$

B. $\frac{1}{x-3}+C$

C. $-\frac{1}{x-3}+C$

D. $\frac{1}{3-x}+C$

Câu 7. Cho hàm $f\left(x\right)=\frac{1}{x^2-3x+2}$. Khi đó:

A. $\int f\left(x\right)dx=\ln \left|\frac{x+1}{x+2}\right|+C$

B. $\int f\left(x\right)dx=\ln \left|\frac{x-1}{x-2}\right|+C$

C. $\int f\left(x\right)dx=\ln \left|\frac{x+2}{x+1}\right|+C$

D. $\int f\left(x\right)dx=\ln \left|\frac{x-2}{x-1}\right|+C$

Câu 8. Họ nguyên hàm F(x) của hàm số $f\left(x\right)=\frac{1}{x^2-4x+3}$ là

A. $F\left(x\right)=\frac{1}{2}\ln \left|\frac{x-3}{x-1}\right|+C$

B. $F\left(x\right)=\frac{1}{2}\ln \left|\frac{x-1}{x-3}\right|+C$

C. $F\left(x\right)=\ln |x^2-4x+3|+C$

D. $F\left(x\right)=\ln |x^2-4x+3|+C$

Câu 9. Gọi F(x) là nguyên hàm của hàm số $f\left(x\right)=\frac{1}{x^2-3x+2}$ thỏa mãn F $\left(\frac{3}{2}\right)$ = 0. Khi đó F(3) bằng:

A. 2ln2

B. ln2

C. -2ln2

D. –ln2

Câu 10. Tìm nguyên hàm của hàm số f(x) biết $f\left(x\right)=\frac{2x+3}{x^2+4x+3}$

A. $-\frac{x^2+3x}{{\left(x^2+4x+3\right)}^2}+C$

B. $(2x+3)\ln \left|x^2+4x+3\right|+C$

C. $\frac{x^2+3x}{x^2+4x+3}+C$

D. $\frac{1}{2}\left(\ln \left|x+1\right|+3\ln \left|x+3\right|\right)+C$

Câu 11. Tính $\int \frac{d\text{x}}{x^2+2\text{x}-3}$

A. $\frac{-1}{4}\ln \left|\frac{x-1}{x+3}\right|+C$

B. $\frac{-1}{4}\ln \left|\frac{x+3}{x-1}\right|+C$

C. $\frac{1}{4}\ln \left|\frac{x+3}{x-1}\right|+C$

D. $\frac{1}{4}\ln \left|\frac{x-1}{x+3}\right|+C$

Câu 12. Họ nguyên hàm của f(x) = $\frac{1}{x(x+1)}$ là:

A. F(x) = ln$\left|\frac{x+1}{x}\right|+C$

B. F(x) = ln$\left|\frac{x}{x+1}\right|+C$

C. F(x) =$\frac{1}{2}\text{ln}\left|\frac{x}{x+1}\right|+C$

D. F(x) = ln$\left|x(x+1)\right|+C$

Câu 13. Nếu F(x) là một nguyên hàm của hàm $f\left(x\right)=\frac{x-3}{x^2+2x-3},F\left(0\right)=0$ thì hằng số C bằng

A. $-\frac{2}{3}\ln 3$

B. $\frac{3}{2}\ln 3$

C. $\frac{2}{3}\ln 3$

D. $-\frac{3}{2}\ln 3$

Câu 14. Nguyên hàm của hàm số: y = $\int \frac{\mathrm{dx}}{a^2-x^2}$ là:

A. $\frac{1}{2a}\ln \left|\frac{a-x}{a+x}\right|$ +C

B. $\frac{1}{2a}\ln \left|\frac{a+x}{a-x}\right|$ +C

C. $\frac{1}{a}\ln \left|\frac{x-a}{x+a}\right|$ +C

D. $\frac{1}{a}\ln \left|\frac{x+a}{x-a}\right|$ +C

Câu 15. Nguyên hàm của hàm số: y =$\int \frac{\mathrm{dx}}{x^2-a^2}$ là:

A. $\frac{1}{2a}\ln \left|\frac{x-a}{x+a}\right|$ +C

B. $\frac{1}{2a}\ln \left|\frac{x+a}{x-a}\right|$ +C

C. $\frac{1}{a}\ln \left|\frac{x-a}{x+a}\right|$ +C

D. $\frac{1}{a}\ln \left|\frac{x+a}{x-a}\right|$ +C

Câu 16. Để tìm họ nguyên hàm của hàm số: $f\left(x\right)=\frac{1}{x^2-6x+5}$. Một học sinh trình bày như sau:

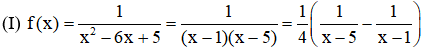
(II) Nguyên hàm của các hàm số $\frac{1}{x-5},\frac{1}{x-1}$ theo thứ tự là: $\ln \left|x-5\right|,\ln \left|x-1\right|$

(III) Họ nguyên hàm của hàm số f(x) là:

Nếu sai, thì sai ở phần nào?

A. I

B. I, II

C. II, III

D. III

Câu 17. Tính: $P=\int \frac{x+1}{\sqrt{x^2+1}}dx$

A. $P=x\sqrt{x^2+1}-x+C$

B. $P=\sqrt{x^2+1}+\ln \left|x+\sqrt{x^2+1}\right|+C$

C. $P=\sqrt{x^2+1}+\ln \left|\frac{1+\sqrt{x^2+1}}{x}\right|+C$

D. Đáp án khác.

Câu 18. Hàm số nào dưới đây là một nguyên hàm của hàm số: $y=\frac{1}{\sqrt{4+x^2}}$

A. $F\left(x\right)=2\sqrt{4+x^2}$

B. $F\left(x\right)=x+2\sqrt{4+x^2}$

C. $F\left(x\right)=\ln \left(x-\sqrt{4+x^2}\right)$

D. $F\left(x\right)=\ln \left(x+\sqrt{4+x^2}\right)$

Câu 19. Tính nguyên hàm $\int \frac{dx}{\sqrt{x^2+a}}$?

A. $\ln \left|x-\sqrt{x^2+a}\right|+C$

B. $\ln \left|2x-\sqrt{x^2+a}\right|+C$

C. $\ln \left|2x+\sqrt{x^2+a}\right|+C$

D. $\ln \left|x+\sqrt{x^2+a}\right|+C$

Câu 20. Nguyên hàm của hàm số $f\left(x\right)=\frac{2x}{{\left(1-x\right)}^3}$

A. $F\left(x\right)=\frac{2}{x-1}+\frac{1}{{\left(x-1\right)}^2}+C$

B. $F\left(x\right)=\frac{2}{x-1}-\frac{1}{{\left(x-1\right)}^2}+C$

C. $F\left(x\right)=\frac{1}{1-x}+\frac{1}{4{\left(1-x\right)}^4}+C$

D. $F\left(x\right)=\frac{1}{1-x}-\frac{1}{4{\left(1-x\right)}^4}+C$

Đáp án