100 công thức logarit đầy đủ, chi tiết nhất (2024) và cách giải các dạng bài tập

Công thức logarit đầy đủ, chi tiết nhất 

1. Lí thuyết

a. Định nghĩa: Cho 2 số dương a, b với $a\ne 1$. Số x thỏa mãn đẳng thức $a^x=b$ được gọi là lôgarit cơ số a của b và kí hiệu là ${\log }_{a}b$

b. Các tính chất: Với $a,b>0;a\ne 1$ ta có

$$\begin{gathered} {\log }_{a}1=0 \\ {\log }_{a}a=1 \\ {a}^{{\log }_{a}b}=b \\ {\log }_a{a}^{\alpha }=\alpha .{\log }_{a}a=\alpha \end{gathered}$$

2. Các quy tắc tính

a. Lôgarit của một tích

•  Định lí 1: Với các số dương a, x, y và $a\ne 1$ ta có:

${\log }_a\left(x.y\right)={\log }_{a}x+{\log }_{a}y$

• Chú ý: Định lí 1 có thể mở rộng cho tích của n số dương:

$$\begin{gathered} {\log }_a\left(x_1.x_2\mathrm{...}{x}_n\right) \\ ={\log }_a{x}_1+{\log }_a{x}_2+\mathrm{...}+{\log }_a{x}_n \\ \left(a,x_i,i=\overline{1,n}>0;a\ne 1\right) \end{gathered}$$

b. Lôgarit của một thương

• Định lí 2: Với các số dương a, x, y và $a\ne 1$ ta có:

${\log }_a\frac{x}{y}={\log }_{a}x-{\log }_{a}y$

c. Lôgarit của một lũy thừa

• Định lí 3: Lôgarit của một lũy thừa bằng tích của số mũ với lôgarit của cơ số.

$$\begin{gathered} {\log }_a{b}^{\alpha }=\alpha .{\log }_{a}b \\ \left(a,b>0;a\ne 1,\alpha \in ℝ\right) \end{gathered}$$

• Đặc biệt:

${\log }_a\sqrt[n]{b}=\frac{1}{n}{\log }_{a}b$

3. Công thức đổi cơ số, lôgarit thập phân và lôgarit tự nhiên.

• Định lí 4: Cho 3 số dương a, b, c với $a\ne 1,c\ne 1$, ta có:

${\log }_{a}b=\frac{{\log }_{c}b}{{\log }_{c}a}$

• Đặc biệt:

$\left\{\begin{array}{l}{\log }_{a}b=\frac{1}{{\log }_{b}a}\left(b\ne 1\right)\\ {\log }_{a^{\alpha }}b=\frac{1}{\alpha }{\log }_{a}b\left(\alpha \ne 0\right)\end{array}\right.$

• Lôgarit thập phân: Là lôgarit cơ số 10. Kí hiệu: ${\log }_{10}x=\log x$
• Lôgarit tự nhiên: Là lôgarit cơ số e. Kí hiệu: ${\log }_{e}x=\ln x$
• Chú ý: Tìm số các chữ số của một lũy thừa:

Bài toán: Số $a^{\alpha }$ có bao nhiêu chữ số?

Số các chữ số của $a^{\alpha }$ chính là $\left[\log a^{\alpha }\right]+1$ (phần nguyên $a^{\alpha }$ cộng 1)

- VD: Số $3^{20}$ có $\left[\log 3^{20}\right]+1=10$ chữ số.

4. Các ví dụ

VD1. Tìm x biết

a. ${\log }_{2}x=3$

b. $3^x=4$

c.  ${\log }_{3}x=4{\log }_{3}a+7{\log }_{3}b$

Lời giải:

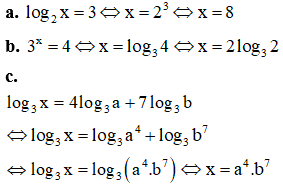
VD2. Cho ${\log }_{3}15=a$ và ${\log }_{3}10=b$. Tính ${\log }_{\sqrt{3}}50$ theo a và b.

Lời giải:

Ta có:

$$\begin{gathered} {\log }_{\sqrt{3}}50={\log }_{3^{\frac{1}{2}}}50 \\ =2{\log }_3\left(5.10\right)=2{\log }_{3}5+2{\log }_{3}10 \end{gathered}$$

Ta thấy:

$$\begin{gathered} {\log }_{3}15=a\iff 1+{\log }_{3}5=a \\ \Rightarrow {\log }_{3}5=a-1 \end{gathered}$$

Thay lại ta được:

$$\begin{gathered} {\log }_{\sqrt{3}}50=2\left(a-1\right)+2b \\ \iff {\log }_{\sqrt{3}}50=2a+2b-2 \end{gathered}$$

VD3. Cho ${\log }_{2}5=a$. Tính ${\log }_{4}1250$ theo a.

Lời giải:

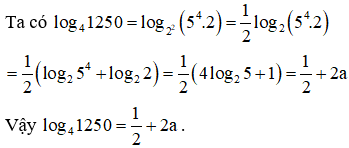
VD4. Cho $a={\log }_{2}3$, $b={\log }_{3}5$, $c={\log }_{7}2$. Tính ${\log }_{140}63$ theo a, b, c

Lời giải:

Ta có:

$$\begin{gathered} {\log }_{140}63=\frac{{\log }_{7}63}{{\log }_{7}140} \\ =\frac{{\log }_7{3}^2.7}{{\log }_7{2}^2\mathrm{.5.7}}=\frac{1+2{\log }_{7}3}{1+2{\log }_{7}2+{\log }_{7}5} \end{gathered}$$

+) ${\log }_{7}3={\log }_{2}3.{\log }_{7}2=a.c$

+) ${\log }_{7}5={\log }_{3}5.{\log }_{7}3=b.a.c$

Thay vào ta được: 

${\log }_{140}63=\frac{1+2ac}{1+2c+abc}$

5. Luyện tập

Bài 1. Tính

a. ${\log }_2\frac{1}{8}$

b. ${\log }_{\frac{1}{4}}2$

c. ${\log }_3\sqrt[4]{3}$

Bài 2. Tính

a. $4^{{\log }_{2}5}$

b. ${27}^{-{\log }_{9}2}$

c. $9^{{\log }_{\sqrt{3}}2}$

Bài 3. Tìm x biết

a. ${\log }_{5}x=2{\log }_{5}a-3{\log }_{5}b$$\left(a,b>0\right)$

b. ${\log }_{\frac{1}{2}}x=\frac{2}{3}{\log }_{\frac{1}{2}}a-\frac{1}{5}{\log }_{\frac{1}{2}}b$$\left(a,b>0\right)$

Bài 4. Tính

a.  $A=\frac{1}{2}{\log }_{7}36-{\log }_{7}14-3{\log }_7\sqrt[3]{21}$

b. $B=\frac{{\log }_{2}24-\frac{1}{2}{\log }_{2}72}{{\log }_{3}18-\frac{1}{3}{\log }_{3}72}$

Bài 5. So sánh các cặp số sau

a.  ${\log }_{3}5$ và ${\log }_{7}4$

b. ${\log }_{2}10$ và ${\log }_{5}30$

Bài 6.

a. ${\log }_{2}5=a$ và ${\log }_{3}5=b$. Tính ${\log }_{6}5$ theo a và b

b. Cho ${\log }_{2}3=a$; ${\log }_{5}3=b$. Hãy biểu diễn ${\log }_{6}45$ theo a và b.