100 bài tập về tọa độ điểm, tọa độ vectơ (2024 có đáp án) và cách giải các dạng toán

Các bài toán về tọa độ điểm, tọa độ vectơ và cách giải 

I. LÝ THUYẾT

1. Hệ trục tọa độ trong không gian

Trong không gian, xét ba trục tọa độ Ox, Oy, Oz vuông góc với nhau từng đôi một và chung một điểm gốc O. Gọi $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ là các vectơ đơn vị, tương ứng trên các trục Ox, Oy, Oz. Hệ ba trục như vậy gọi là hệ trục tọa độ vuông góc trong không gian.

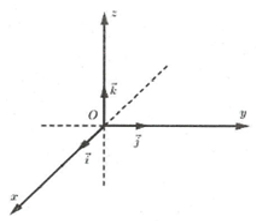
Điểm O được gọi là gốc tọa độ.

Các mặt phẳng (Oxy); (Oyz); (Oxz) đôi một vuông góc với nhau được gọi là các mặt phẳng tọa độ.

Chú ý: ${\overrightarrow{i}}^2={\overrightarrow{j}}^2={\overrightarrow{k}}^2=1$

và $\overrightarrow{i}.\overrightarrow{j}=\overrightarrow{i}.\overrightarrow{k}=\overrightarrow{k}.\overrightarrow{j}=0$

2. Tọa độ của vectơ

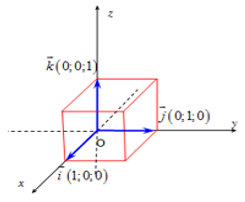
a) Định nghĩa:

$$\begin{gathered} \overrightarrow{u}=\left(x;y;z\right) \\ \iff \overrightarrow{u}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k} \end{gathered}$$

b) Tính chất:

Cho $\overrightarrow{a}=(a_1;a_2;a_3),\overrightarrow{b}=(b_1;b_2;b_3),k\in ℝ$ ta có:

+ Tổng và hiệu của hai vectơ:

$\overrightarrow{a}\pm \overrightarrow{b}=(a_1\pm b_1;a_2\pm b_2;a_3\pm b_3)$

+ Tích của vectơ với một số:

$k\overrightarrow{a}=(k{a}_1;k{a}_2;k{a}_3)$ $\left(k\in ℝ\right)$

+ Hai vectơ bằng nhau:

$\overrightarrow{a}=\overrightarrow{b}\iff \left\{\begin{array}{l}{a}_1=b_1\\ a_2=b_2\\ a_3=b_3\end{array}\right.$

+ Chú ý:

$$\begin{gathered} \overrightarrow{0}=(0;0;0),\overrightarrow{i}=(1;0;0), \\ \overrightarrow{j}=(0;1;0),\overrightarrow{k}=(0;0;1) \end{gathered}$$

+ $\overrightarrow{a}$ cùng phương $\overrightarrow{b}(\overrightarrow{b}\ne \overrightarrow{0})\text{\hspace{0.17em}⇔\hspace{0.17em}}\overrightarrow{a}=k\overrightarrow{b}(k\in ℝ)$

3. Tọa độ của điểm

a) Định nghĩa: M(x; y; z) $\iff \overrightarrow{OM}=x.\overrightarrow{i}+y.\overrightarrow{j}+z.\overrightarrow{k}$ (x: hoành độ, y: tung độ, z: cao độ).

Chú ý:

$$\begin{gathered} M\in \left(Oxy\right)\iff z=0; \\ M\in \left(Oyz\right)\iff x=0; \\ M\in \left(Oxz\right)\iff y=0 \end{gathered}$$

$$\begin{gathered} M\in Ox\iff y=z=0; \\ M\in Oy\iff x=z=0; \\ M\in Oz\iff x=y=0 \end{gathered}$$

b) Tính chất: Cho $A(x_A;y_A;z_A),B(x_B;y_B;z_B)$

II. PHƯƠNG PHÁP GIẢI

Sử dụng các định nghĩa, tính chất và các khái niệm có liên quan đến điểm, vectơ bao gồm: tọa độ của điểm, vectơ; các phép toán vectơ… để tính tổng, hiệu các vectơ, tìm tọa độ trung điểm của đoạn thẳng, trọng tâm của tam giác, tìm điểm và vectơ thỏa mãn điều kiện cho trước, …

III. VÍ DỤ MINH HỌA

Ví dụ 1: Trong không gian với hệ trục tọa độ Oxyz cho A (1; 2; 0); B (3; -1; 1) và C (1; 1; 1). Tính tọa độ trọng tâm G của tam giác ABC.

A. $G\left(\frac{5}{3};\frac{2}{3};\frac{2}{3}\right)$

B. $G\left(-\frac{5}{3};\frac{2}{3};\frac{2}{3}\right)$

C. $G\left(\frac{5}{3};-\frac{2}{3};\frac{2}{3}\right)$

D. $G\left(\frac{5}{3};-\frac{2}{3};-\frac{2}{3}\right)$

Hướng dẫn giải

Áp dụng công thức tọa độ trọng tâm trong tam giác ABC ta có:

Tọa độ trọng tâm $G\left(\frac{1+3+1}{3};\frac{2-1+1}{3};\frac{0+1+1}{3}\right)$ hay $G\left(\frac{5}{3};\frac{2}{3};\frac{2}{3}\right)$

Chọn A.

Ví dụ 2: Trong không gian Oxyz, tìm toạ độ của vectơ $\overrightarrow{u}=\overrightarrow{i}+2\overrightarrow{j}-\overrightarrow{k}$.

A. $\overrightarrow{u}=\left(1;2;-1\right)$

B. $\overrightarrow{u}=\left(-1;2;1\right)$

C. $\overrightarrow{u}=\left(2;1;-1\right)$

D. $\overrightarrow{u}=\left(-1;1;2\right)$

Hướng dẫn giải

Ta có

$$\begin{gathered} \overrightarrow{i}=\left(1;0;0\right), \\ \overrightarrow{j}=\left(0;1;0\right), \\ \overrightarrow{k}=\left(0;0;1\right) \end{gathered}$$

Nên $\overrightarrow{u}=\overrightarrow{i}+2\overrightarrow{j}-\overrightarrow{k}$

$$\begin{gathered} =(1;0;0)+2\left(0;1;0\right)-\left(0;0;1\right) \\ =\left(1;2;-1\right) \end{gathered}$$

Chọn A.

Ví dụ 3: Trong không gian với hệ tọa độ Oxyz, cho ba điểm M (0; 1; 2), N (7; 3; 2), P (-5; -3; 2). Tìm tọa độ điểm Q thỏa mãn $\overrightarrow{MN}=\overrightarrow{QP}$.

A. Q (12; 5; 2).

B. Q (-12; 5; 2).

C. Q (-12; -5; 2).

D. Q (-2; -1; 2).

Hướng dẫn giải

Ta có:

$$\begin{gathered} \overrightarrow{MN}=\overrightarrow{QP}\iff \left\{\begin{array}{l}{x}_N-x_M=x_P-x_Q\\ y_N-y_M=y_P-y_Q\\ z_N-z_M=z_P-z_Q\end{array}\right. \\ \iff \left\{\begin{array}{l}7-0=-5-x_Q\\ 3-1=-3-y_Q\\ 2-2=2-z_Q\end{array}\right. \\ \iff \left\{\begin{array}{l}7=-5-x_Q\\ 2=-3-y_Q\\ 0=2-z_Q\end{array}\right.\iff \left\{\begin{array}{l}{x}_Q=-12\\ y_Q=-5\\ z_Q=2\end{array}\right. \end{gathered}$$

Vậy Q (-12 ; -5 ; 2)

Chọn C.

IV. BÀI TẬP ÁP DỤNG

Câu 1: Trong không gian Oxyz, tìm toạ độ của véctơ $\overrightarrow{u}=5\overrightarrow{i}-3\overrightarrow{j}+\overrightarrow{k}$

A. $\overrightarrow{u}=\left(5;-3;1\right)$

B. $\overrightarrow{u}=\left(-5;3;1\right)$

C. $\overrightarrow{u}=\left(2;1;-1\right)$

D. $\overrightarrow{u}=\left(-1;1;2\right)$

Câu 2: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có ba đỉnh A (2; 1; -3), B (4; 2; 1), C (3; 0; 5) và G (a; b; c) là trọng tâm của tam giác ABC. Tính giá trị biểu thức P = a.b.c?

A. P = 0.

B. P = 3.

C. P = 5.

D. P = 4.

Câu 3: Trong không gian với hệ tọa độ Oxyz, cho hai vectơ $\overrightarrow{a}=\left(1;2;3\right)$ và $\overrightarrow{b}=2\overrightarrow{i}-4\overrightarrow{k}$. Tính tọa độ vectơ$\overrightarrow{u}=\overrightarrow{a}-\overrightarrow{b}$

A. $\overrightarrow{u}=\left(-1;2;7\right)$

B. $\overrightarrow{u}=\left(-1;6;3\right)$

C. $\overrightarrow{u}=\left(-1;2;-1\right)$

D. $\overrightarrow{u}=\left(-1;-2;3\right)$

Câu 4: Trong không gian Oxyz, cho điểm M (1; 2; 3). Tìm tọa độ hình chiếu M lên trục Ox.

A. (2; 0; 0)

B. (1; 0; 0)

C. (3; 0; 0)

D. (0; 2; 3)

Câu 5: Trong không gian với hệ tọa độ Oxyz, cho điểm M (1; 2; 3). Tìm tọa độ điểm N đối xứng với điểm M qua mặt phẳng (Oxy)

A. N (-1; -2; -3)

B. N (1; 2; 0)

C. N (-1; -2; 3)

D. N (1; 2; -3)

Câu 6: Trong không gian với hệ trục tọa độ Oxyz cho điểm I (-5; 0; 5) là trung điểm của đoạn MN, biết M (1; -4; 7). Tìm tọa độ của điểm N.

A. N ( -10; 4; 3)

B. N (-2; -2; 6)

C. N (-11; -4; 3)

D. N (-11; 4; 3).

Câu 7: Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (0; 1; 2), B (7; 3; 2), C (-5; -3; 2). Tìm tọa độ điểm D thỏa mãn $\overrightarrow{AB}=\overrightarrow{CD}$

A. D (2; -1; 2)

B. D (-12; 5; 2)

C. D (-12; -5; 2)

D. D (-2; -1; 2)

Câu 8: Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A (3; 2; 1), B (1; -1; 2), C (1; 2; -1). Tìm tọa độ điểm M thỏa mãn $\overrightarrow{OM}=2\overrightarrow{AB}-\overrightarrow{AC}$

A. M (-2; 6; -4)

B. M (2; -6; 4)

C. M (-2; -6; 4)

D. M (5; 5; 0)

Câu 9: Trong không gian với hệ tọa độ Oxyz, cho hai véc tơ $\overrightarrow{v}=\left(2;5;-1\right)$ và $\overrightarrow{u}=\left(-1;3;-2\right)$. Tìm tọa độ của véc tơ $\overrightarrow{a}=2\overrightarrow{u}-3\overrightarrow{v}$

A. $\overrightarrow{a}=\left(-8;9;-1\right).$

B. $\overrightarrow{a}=\left(-8;-9;1\right).$

C. $\overrightarrow{a}=\left(8;-9;-1\right).$

D. $\overrightarrow{a}=\left(-8;-9;-1\right).$

Câu 10: Trong không gian với hệ tọa độ Oxyz, cho hình bình hành MNPQ có M (2; 0; 0), N (0; -3; 0), P (0; 0; -4). Tìm tọa độ điểm Q.

A. Q (-2; -3; -4)

B. Q (2; 3; -4)

C. Q (-2; -3; 4)

D. Q (4; 4; 2)

ĐÁP ÁN