100 công thức về xét tính đồng biến, nghịch biến của đồ thị hàm số (2024)

Công thức xét tính đồng biến, nghịch biến của hàm số chi tiết nhất 

1. Lý thuyết

Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f(x) xác định trên K ta có:

+ Hàm số y = f(x) được gọi là đồng biến (tăng) trên K nếu:

$$\begin{gathered} \forall x_1,x_2\in K,x_1<x_2 \\ \Rightarrow f\left(x_1\right)<f\left(x_2\right) \end{gathered}$$

+ Hàm số y = f(x) được gọi là nghịch biến (giảm) trên K nếu:

$$\begin{gathered} \forall x_1,x_2\in K,x_1<x_2 \\ \Rightarrow f\left(x_1\right)>f\left(x_2\right) \end{gathered}$$

Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K.

Nhận xét:

+ Hàm số f(x) đồng biến trên K:

$$\begin{gathered} \iff \frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}>0\forall x_1,x_2\in K, \\ {x}_1\ne x_2. \end{gathered}$$

Khi đó đồ thị của hàm số đi lên từ trái sang phải.

+ Hàm số f(x) nghịch biến trên K :

$$\begin{gathered} \iff \frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}<0\forall x_1,x_2\in K, \\ {x}_1\ne x_2. \end{gathered}$$

Khi đó đồ thị của hàm số đi xuống từ trái sang phải.

⁕ Ứng dụng đạo hàm để xét tính đơn điệu của hàm số:

• Nếu $f^{\text{'}}\left(x\right)>0,\forall x\in \left(a;b\right)\Rightarrow$ hàm số f(x) đồng biến trên khoảng (a; b)

• Nếu $f^{\text{'}}\left(x\right)<0,\forall x\in \left(a;b\right)\Rightarrow$ hàm số f(x) nghịch biến trên khoảng (a; b)

• Nếu $f^{\text{'}}\left(x\right)=0,\forall x\in \left(a;b\right)\Rightarrow$ hàm số f(x) không đổi trên khoảng (a; b)

• Nếu f(x) đồng biến trên khoảng:

$\left(a;b\right)\Rightarrow f^{\text{'}}\left(x\right)\ge 0,\forall x\in \left(a;b\right).$

• Nếu f(x) nghịch biến trên khoảng:

$\left(a;b\right)\Rightarrow f^{\text{'}}\left(x\right)\le 0,\forall x\in \left(a;b\right).$

• Nếu thay đổi khoảng (a; b) bằng một đoạn hoặc nửa khoảng thì phải bổ sung thêm giả thiết “hàm số f(x) liên tục trên đoạn hoặc nửa khoảng đó”.

2. Quy tắc xét tính đơn điệu của hàm số

Giả sử hàm số f có đạo hàm trên K

• Nếu $f^{\text{'}}\left(x\right)\ge 0$ với mọi $x\in K$ và $f^{\text{'}}\left(x\right)=0$ chỉ tại một số hữu hạn điểm $x\in K$ thì hàm số f đồng biến trên K.

• Nếu $f^{\text{'}}\left(x\right)\le 0$ với mọi $x\in K$ và $f^{\text{'}}\left(x\right)=0$ chỉ tại một số hữu hạn điểm $x\in K$ thì hàm số f đồng biến trên K.

Phương pháp giải chung

Bước 1. Tìm tập xác định D của hàm số. Tính đạo hàm $y^{\text{'}}=f^{\text{'}}\left(x\right)$.

Bước 2. Tìm các điểm tại đó $f^{\text{'}}\left(x\right)=0$ hoặc $f^{\text{'}}\left(x\right)$ không xác định.

Bước 3. Sắp xếp các điểm theo thứ tự tăng dần và lập bảng xét dấu của y'.

Dựa vào quy tắc xét dấu đã nêu để xét dấu cho y'.

Bước 4. Kết luận về các khoảng đồng biến và nghịch biến dựa vào bảng xét dấu của y'.

Chú ý:

• Đối với hàm phân thức hữu tỉ $y=\frac{ax+b}{cx+d}\left(x\ne -\frac{d}{c}\right)$ thì dấu “=” khi xét dấu đạo hàm y' không xảy ra.

• Giả sử:

$y=f\left(x\right)=a{x}^3+b{x}^2+cx+d$

$\Rightarrow f^{\text{'}}\left(x\right)=3a{x}^2+2bx+c.$

+ Hàm số đồng biến trên R

$$\begin{gathered} \iff f^{\text{'}}\left(x\right)\ge 0;\forall x\in ℝ \\ \iff \left[\begin{array}{l}\left\{\begin{array}{l}a>0\\ \Delta \le 0\end{array}\right.\\ \left\{\begin{array}{l}a=0\\ b=0\\ c>0\end{array}\right.\end{array}\right.. \end{gathered}$$

+ Hàm số nghịch biến trên R

$$\begin{gathered} \iff f^{\text{'}}\left(x\right)\le 0;\forall x\in ℝ \\ \iff \left[\begin{array}{l}\left\{\begin{array}{l}a<0\\ \Delta \le 0\end{array}\right.\\ \left\{\begin{array}{l}a=0\\ b=0\\ c<0\end{array}\right.\end{array}\right.. \end{gathered}$$

Trường hợp 2 thì hệ số c khác 0 vì khi a = b = c = 0 thì f(x) = d

(Đường thẳng song song hoặc trùng với trục Ox thì không đơn điệu)

• Với dạng toán tìm tham số m để hàm số bậc ba đơn điệu một chiều trên khoảng có độ dài bằng 1 ta giải như sau:

Bước 1: Tính $y^{\text{'}}=f^{\text{'}}\left(x;m\right)=a{x}^2+bx+c.$

Bước 2: Hàm số đơn điệu trên $\left(x_1;x_2\right)\iff y^{\text{'}}=0$ có 2 nghiệm phân biệt

$\iff \left\{\begin{array}{l}\Delta >0\\ a\ne 0\end{array}\right.\left(*\right)$

Bước 3: Hàm số đơn điệu trên khoảng có độ dài bằng 1

$$\begin{gathered} \iff \left|x_1-x_2\right|=l \\ \iff {\left(x_1+x_2\right)}^2-4x_1{x}_2=l^2 \\ \iff S^2-4P=l^2\left(**\right) \end{gathered}$$

Bước 4: Giả (*) và giao với (* *) để suy ra giá trị m cần tìm.

3. Một số ví dụ

Ví dụ 1: Tìm các khoảng đồng biến và nghịch biến của các hàm số sau

a) $y=x+\frac{4}{x}$.

b) $y=\frac{x^2-x+9}{x-1}$.

Lời giải

a) TXĐ: $D=ℝ\backslash \left\{0\right\}$.

Ta có:

$$\begin{gathered} y^{\text{'}}=1-\frac{4}{x^2}=0 \\ \iff \left\{\begin{array}{l}x=2\\ x=-2\end{array}\right. \end{gathered}$$

Bảng biến thiên (xét dấu $y^{\text{'}}$):

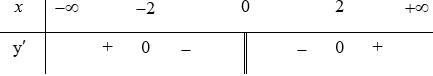
Vậy hàm số đồng biến trên các khoảng $\left(-\infty ;-2\right)$ và $\left(2;+\infty \right)$, hàm số nghịch biến trên khoảng (– 2; 0) và (0; 2).

b) TXĐ: $D=ℝ\backslash \left\{1\right\}$

Ta có:

$$\begin{gathered} y^{\text{'}}=\frac{\left(2x-1\right)\left(x-1\right)-\left(x^2-x+9\right)}{{\left(x-1\right)}^2} \\ =\frac{x^2-2x-8}{{\left(x-1\right)}^2}=0\iff \left\{\begin{array}{l}x=-2\\ x=4\end{array}\right. \end{gathered}$$

Bảng biến thiên (xét dấu):

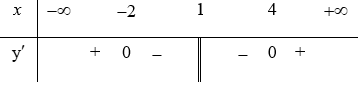
Vậy hàm số đồng biến trên các khoảng $\left(-\infty ;-2\right)$ và $\left(4;+\infty \right)$, hàm số nghịch biến trên các khoảng (– 2; 1) và (1; 4).

Ví dụ 2: Tìm các khoảng đồng biến và nghịch biến của các hàm số sau:

a) $y=x^3-3x^2+2$

b) $y=x^4-2x^2$

Lời giải

a) TXĐ: $D=ℝ$

Ta có:

$y^{\text{'}}=3x^2-6x\iff \left\{\begin{array}{l}x=0\\ x=2\end{array}\right.$

Bảng biến thiên (xét dấu):

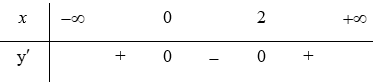
Vậy hàm số đồng biến trên các khoảng $\left(-\infty ;0\right)$ và $\left(2;+\infty \right)$, nghịch biến trên khoảng (0; 2).

b) TXĐ: $D=ℝ$

Ta có:

$y^{\text{'}}=4x^3-4x\iff \left\{\begin{array}{l}x=0\\ x=\pm 1\end{array}\right.$

Bảng biến thiên (xét dấu):

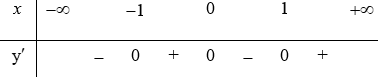
Vậy hàm số đồng biến trên các khoảng $\left(-1;0\right)$ và $\left(1;+\infty \right)$, nghịch biến trên khoảng $\left(-\infty ;-1\right)$ và (0; 1).

4. Luyện tập

Bài 1. Tìm các khoảng đồng biến và nghịch biến của các hàm số sau:

a) $y=-x^2+2x+5$

b) $y=\frac{1}{3}{x}^3+3x^2-7x+2$

Bài 2. Tìm các khoảng đơn điệu của các hàm số:

a) $y=\frac{1+x}{2-x}$

b) $y=\frac{x^2+3x}{1-x}$

Bài 3. Tìm các khoảng đơn điệu của các hàm số:

a) $y=-x^4+2x^2-3$

b) $y=\sqrt{x^2+x-6}$

Bài 4. Chứng minh rằng hàm số $\sin x-x$ nghịch biến trên nửa khoảng $\left[0;\frac{\pi }{2}\right)$

Bài 5. Tìm m để hàm số $y=\frac{1}{3}{x}^3-m{x}^2+\left(2m+3\right)x-2$ đồng biến trên R