100 bài tập về Hệ thức Vi-et và công thức Hệ thức Vi-et (2024 có đáp án) và cách giải các dạng toán

Bài tập về Hệ thức Vi-et và công thức Hệ thức Vi-et hay nhất

I. Lí thuyết tổng hợp

- Định lí Vi- ét:

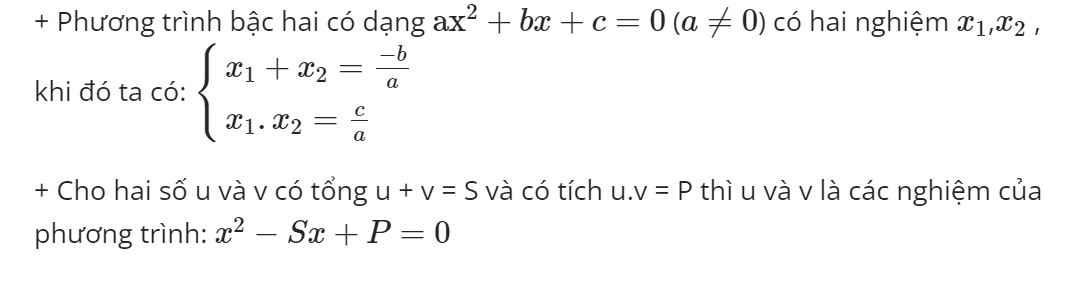
II. Các công thức

- Định lí Vi-ét:

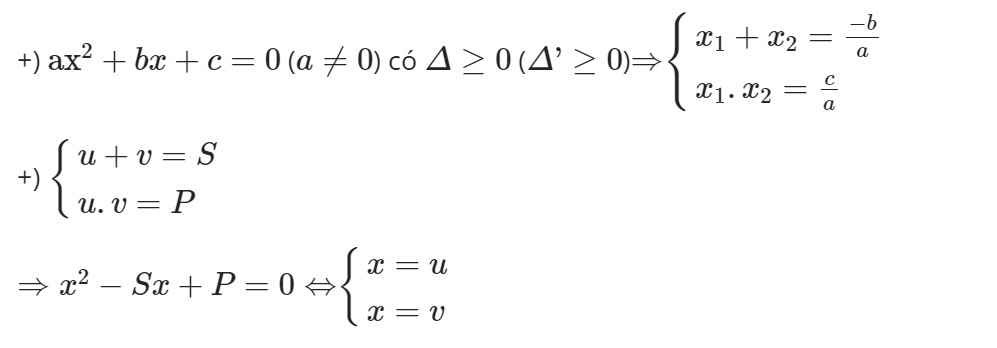
- Dấu của nghiệm phương trình bậc hai:

III. Ví dụ minh họa

Bài 1: Cho phương trình x²+4x+2=0 . Tìm giá trị biểu thức 1/x + 1/x² mà không cần phải tìm nghiệm của phương trình với x₁; x₂ là hai nghiệm của phương trình đã cho.

Lời giải:

Bài 2: Cho phương trình x²+2mx+2m−1=0. Tìm m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn: x₁²+x₂²=6

Lời giải:

Xét phương trình:x²+2mx+2m−1=0

Δ'=m²−1.(2m−1) = m_²−2m+1=(m−1)2≥0 ∀m∈R

⇒ Phương trình có hai nghiệm phân biệt x₁ 𝑥₂ ⇔m≠1

Bài 3: Tìm m thỏa mãn các điều kiện sau:

a) x²+4x−2m=0 có hai nghiệm phân biệt trái dấu.

b) x²+mx−m−1=0 có hai nghiệm phân biệt cùng dấu.

c) x²+mx−m−1=0 có hai nghiệm phân biệt dương.

d) 2x²+3mx−2=0 có hai nghiệm phân biệt âm.

Lời giải:

a)

Xét phương trình x²+4x−2m=0

Để phương trình có hai nghiệm phân biệt trái dấu thì 1.(−2m)<0⇔m>0

Vậy m > 0 thì phương trình đã cho có hai nghiệm phân biệt trái dấu.

b)

Xét phương trình x²+mx−m−1=0

Để phương trình có hai nghiệm phân biệt thì

Δ=m²−4.1.(−m−1)=m2+4m+4=(m+2)2>0⇔m≠−2 (1)

Áp dụng định lí Vi-ét ta có:

x1.x2= \(\dfrac{-m-1}{1}\)=−m−1

Để phương trình có hai nghiệm phân biệt cùng dấu:

⇒−m−1>0⇔m<−1 (2)

Kết hợp hai điều kiện (1), (2) ta có m < -1 và m≠−2 thì phương trình x²+mx−m−1=0 có hai nghiệm phân biệt cùng dấu.

c)

Xét phương trình x2+mx−m−1=0𝑥2+𝑚𝑥−𝑚−1=0

Để phương trình có hai nghiệm phân biệt thì

Δ=m2−4.1.(−m−1)=m2+4m+4=(m+2)2>0⇔m≠−2 (1)𝛥=𝑚2−4.1.(−𝑚−1)=𝑚2+4𝑚+4=(𝑚+2)2>0⇔𝑚≠−2 (1)

Áp dụng định lí Vi-ét ta có:

{x1+x2=−m1=−mx1.x2=−m−11=−m−1𝑥1+𝑥2=−𝑚1=−𝑚𝑥1.𝑥2=−𝑚−11=−𝑚−1

Để phương trình có hai nghiệm phân biệt dương:

⇒{−m>0−m−1>0⇔{m<0m<−1⇔m<−1 (2)⇒−𝑚>0−𝑚−1>0⇔𝑚<0𝑚<−1⇔𝑚<−1 (2)

Kết hợp hai điều kiện (1), (2) ta có m < -1 và m≠−2𝑚≠−2 thì phương trình x2+mx−m−1=0𝑥2+𝑚𝑥−𝑚−1=0 có hai nghiệm phân biệt dương.

d)

Xét phương trình 2x2+3mx−2=02𝑥2+3𝑚𝑥−2=0

Để phương trình có hai nghiệm phân biệt thì

Δ=(3m)2−4.2.(−2)=9m2+16>0∀m∈R𝛥=(3𝑚)2−4.2.(−2)=9𝑚2+16>0∀𝑚∈ℝ

Áp dụng định lí Vi-ét ta có:

{x1+x2=−3m2x1.x2=−22=−1𝑥1+𝑥2=−3𝑚2𝑥1.𝑥2=−22=−1

Để phương trình có hai nghiệm phân biệt âm:

⇒{−3m2<0−1>0⇒−3𝑚2<0−1>0 (vô lý vì – 1 < 0)

Vậy phương trình không thể có hai nghiệm phân biệt âm.

IV. Bài tập tự luyện

Bài 1: Cho phương trình 4x2−4mx−2m=04𝑥2−4𝑚𝑥−2𝑚=0. Tìm m để phương trình có hai nghiệm dương phân biệt.

Bài 2: Cho phương trình x2−2(m+1)x+3m=0𝑥2−2(𝑚+1)𝑥+3𝑚=0. Tìm m để phương trình có hai nghiệm phân biệt thỏa mãn x1=2x2𝑥1=2𝑥2.

Bài 3: Cho phương trình

 (1)

a) Chứng minh rằng phương trình (1) luôn có hai nghiệm phân biệt với mọi giá trị của m;

b) Tính theo tham số m giá trị của biểu thức

Bài 4: Cho phương trình bậc hai  (x là ẩn số, m là tham số)

a) Chứng minh phương trình trên luôn có 2 nghiệm phân biệt x₁, x₂ với mọi m,

b) Tìm m để hai nghiệm x₁, x₂ của phương trình có tổng hai nghiệm bằng 6

Bài 5: Cho phương trình  (x là ẩn số, m là tham số)

a, Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi m.

b, Tìm m để hai nghiệm phân biệt của phương trình thỏa mãn  có giá trị nhỏ nhất.

Bài 6: Tìm m để phương trình  có hai nghiệm phân biệt thỏa mãn .

Bài 7: Cho phương trình . Tìm m để phương trình có hai nghiệm phân biệt x₁, x₂ thỏa mãn