100 công thức về bán kính của hình nón (2024 có đáp án) và cách giải các dạng toán

Công thức tính bán kính của hình nón đầy đủ, chi tiết nhất

1. Lí thuyết

- Hình nón tròn xoay

Cho tam giác OIM vuông tại I. Khi quay tam giác đó xung quanh cạnh OI thì đường gấp khúc OMI tạo thành một hình được gọi là hình nón tròn xoay, gọi tắt là hình nón.

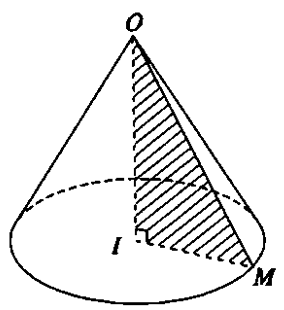
Hình tròn tâm I sinh bởi các điểm thuộc cạnh IM quay quanh trục OI được gọi là mặt đáy của hình nón.

O là đỉnh của hình nón.

OI gọi là chiều cao của hình nón. Kí hiệu h

OM là độ dài đường sinh. Kí hiệu l

IM là bán kính đáy. Kí hiệu r.

2. Các công thức tính bán kính đáy của hình nón

a. Cho chiều cao h và độ dài đường sinh l

- Dựa vào định nghĩa: 

$l^2=h^2+r^2\Rightarrow r=\sqrt{l^2-h^2}$

VD1. Cho hình nón có chiều cao là 4 và độ dài đường sinh bằng 5. Tính chu vi đường tròn đáy của hình nón.

Lời giải:

Bán kính đáy của hình nón là: 

$r=\sqrt{l^2-h^2}=\sqrt{5^2-4^2}=3$

Suy ra chu vi đáy là $C=2\pi r=6\pi$

VD2. Cho hình nón có đường cao bằng 2 lần bán kính đáy và độ dài đường sinh là $l=2\sqrt{5}$. Tính độ dài bán kính đáy.

Lời giải:

Độ dài đường cao là 2r

Ta có:

$$\begin{gathered} l^2=h^2+r^2 \\ \iff 20=5r^2\iff r=2 \end{gathered}$$

Vậy bán kính đáy bằng 2.

b. Góc giữa đường sinh và đáy bằng α

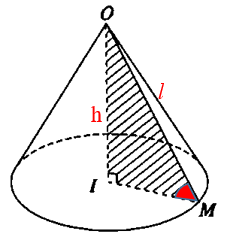
- Góc giữa đường sinh và đáy chính là $\widehat{OMI}$

Khi đó: 

$\left[\begin{array}{l}r=h.\cot \alpha \\ r=l.\cos \alpha \end{array}\right.$

VD1. Tính bán kính đáy của hình nón có chiều cao là a và

Góc giữa đường sinh với đáy bằng ${30}^{\circ }$

Lời giải:

Bán kính 

$$\begin{gathered} r=h.\cot \alpha \\ \Rightarrow r=a.\cot {30}^{\circ }=a\sqrt{3} \end{gathered}$$

VD2. Tính bán kính đường tròn đáy biết độ dài đường sinh bằng 4 và góc giữa đường sinh và đáy là ${60}^{\circ }$

Lời giải:

Bán kính:

$r=l.\cos \alpha =4.\cos {60}^{\circ }=2$

c. Mặt phẳng (P) qua đỉnh và tạo với đáy một góc α

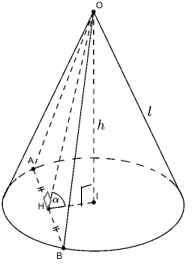
Mp (P) qua O và cắt đáy tại A và B. Gọi H là trung điểm AB

Khi đó $\alpha =\widehat{OHI}$

$$\begin{gathered} \Rightarrow IH=h.\cot \alpha \\ \Rightarrow r=IA=\sqrt{I{H}^2+A{H}^2\text{}} \end{gathered}$$

VD. Cho hình nón đỉnh O đường cao $OI=a\sqrt{3}$. Mặt phẳng (P) qua O và cắt hình nón theo thiết diện là tam giác vuông. Biết góc giữa (P) và đáy bằng ${60}^{\circ }$. Tính bán kính đáy của hình nón.

Lời giải:

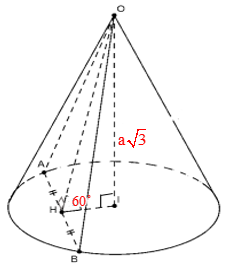
d. Thiết diện qua trục là một tam giác vuông

$r=h=\frac{l\sqrt{2}}{2}$

VD. Cho hình nón có độ dài đường sinh bằng $2\sqrt{2}$. Biết thiết diện qua trục là một tam giác vuông. Tính độ dài bán kính đáy và đường cao của hình nón

Lời giải:

Ta có: 

$r=h=\frac{l\sqrt{2}}{2}=\frac{2\sqrt{2}.\sqrt{2}}{2}=2$