100 công thức tính tích phân cơ bản, đẩy đủ, chi tiết nhất (2024) và cách giải các dạng toán
Công thức và cách giải các dạng toán về tính tích phân gồm phương pháp giải, ví dụ minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập các dạng toán về tính tích phân . Mời các bạn đón xem:
Công thức tính tích phân cơ bản đầy đủ, chi tiết nhất
1. Lý thuyết
a) Định nghĩa:
Cho f là hàm số liên tục trên đoạn [a;b]; Giả sử F là một nguyên hàm của f trên [ a;b]. Hiệu số F(b)-F(a) được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn [a;b] của hàm số f(x), kí hiệu là
Ta dùng kí hiệu để chỉ hiệu số F(b)-F(a).
Vậy
Nhận xét: Tích phân của hàm số f từ a đến b có thể kí hiệu bởi hay Tích phân đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào cách ghi biến số.
- Ý nghĩa hình học: Nếu hàm số y = f(x) liên tục và không âm trên đoạn [a; b] thì diện tích S của hình thang cong giới hạn bởi đồ thị của y = f(x), trục Ox và hai đường thẳng x = a, x = b là:
b) Tính chất của tích phân
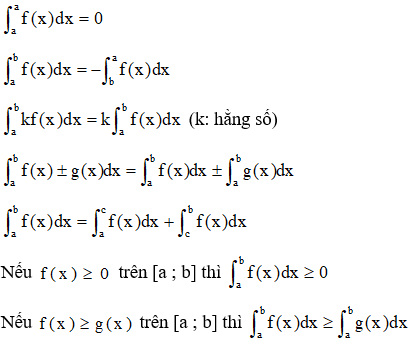
2. Ví dụ minh họa
Ví dụ 1: Tính các tích phân sau:
a)
b)
c)
d)
Lời giải
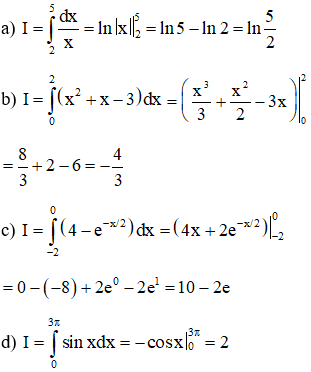
Ví dụ 2: Tính các tích phân sau:
a)
b)
c)
Lời giải
