100 bài tập về phép quay (2024 có đáp án) và cách giải các dạng toán

I. Lý thuyết ngắn gọn

1. Cho điểm O và góc lượng giác $\alpha$. Phép biến hình biến O thành chính nó và biến mỗi điểm M khác O thành điểm M′ sao cho OM′ = OM và góc lượng giác (OM; OM')=$\alpha$ được gọi là phép quay tâm O, $\alpha$ được gọi là góc quay

Kí hiệu: $Q_{\left(O;\alpha \right)}$

Khi $\alpha =2k\pi ,k\in Z$ thì $Q_{\left(O;\alpha \right)}$ là phép đồng nhất

Khi $\alpha =(2k+1)\pi ,k\in Z$ thì $Q_{\left(O;\alpha \right)}$ là phép đối xứng tâm O

2. Trong mặt phẳng Oxy, giả sử M (x; y) và $M\text{'}(x\text{'};y\text{'})=Q_{(O,\alpha )}\left(M\right)$ thì

$\left\{\begin{array}{l}x\text{'}=x\cos \alpha -y\sin \alpha \\ y\text{'}=x\sin \alpha +ycos\alpha \end{array}\right.$

Trong mặt phẳng Oxy, giả sử M (x; y) và I (a; b) và $M\text{'}(x\text{'};y\text{'})=Q_{(I,\alpha )}\left(M\right)$ thì

$\left\{\begin{array}{l}x\text{'}=a+(x-a)cos\alpha -(y-b)\sin \alpha \\ y\text{'}=b+(x-a)\sin \alpha +(y-b)cos\alpha \end{array}\right.$

3. Các tính chất của phép quay:- Bảo toàn khoảng cách giữa hai điểm bất kì- Biến một đường thẳng thành đường thẳng- Biến một đoạn thẳng thành đoạn thẳng bằng đoạn đã cho- Biến một tam giác thành tam giác bằng tam giác đã cho- Biến đường tròn thành đường tròn có cùng bán kính

II. Các dạng toán về phép quay

2.1 Dạng 1: Xác định ảnh của một hình qua phép quay

Phương pháp giải: Sử dụng định nghĩa phép quay, biểu thức tọa độ của phép quay và các tính chất của phép quay $90°$

Ví dụ 1: Tìm ảnh của điểm A (3; 4) qua phép quay tâm O góc quay

Lời giải

Với phép quay tâm O góc 90 độ điểm A thành A’(x; y) có tọa độ thỏa mãn:

$$\begin{gathered} \left\{\begin{array}{l}OA=OA\text{'}\\ (OA;OA\text{'})=90°\end{array}\right. \\ \Rightarrow \left\{\begin{array}{l}{3}^2+4^2=x^2+y^2\\ \overrightarrow{OA}.\overrightarrow{OA\text{'}}=0\end{array}\right. \\ \iff \left\{\begin{array}{l}{x}^2+y^2=25\\ 3x+4y=0\end{array}\right. \\ \iff \left[\begin{array}{l}\left\{\begin{array}{l}x=-4\\ y=3\end{array}\right.\\ \left\{\begin{array}{l}x=4\\ y=-3\end{array}\right.\end{array}\right. \end{gathered}$$

Do $\alpha =90°>0$ phép quay theo chiều dương suy ra: A’ (-4; 3)

Ví dụ 2: Trong mặt phẳng Oxy cho điểm M (2; 0) và đường thẳng d: x + 2y – 2 = 0. Xét phép quay Q tâm O góc quay $90°$

a. Tìm ảnh của điểm M qua phép quay Qb. Tìm ảnh của d qua phép quay Q

Lời giải

a. Ta có vì $M(2;0)\in Ox$$\Rightarrow Q_{(O;90°)}\left(M\right)=M\text{'}:\left\{\begin{array}{l}M\text{'}\in Oy\\ OM=OM\text{'}\end{array}\right.$$\Rightarrow M\text{'}(0;2)$

b. Ta có $M(2;0)\in d$, ảnh của M qua phép quay Q theo câu a là M’ (0; 2)

Gọi d’ là ảnh của d qua Q ta có d’ là đường thẳng qua M’ và vuông góc với d

Đường thẳng d có VTPT là $\overrightarrow{n}=(1;2)$ suy ra d’ có VTPT là $\overrightarrow{n\text{'}}=(2;-1)$

Vậy phương trình của d’ là: $2(x-0)-1(y-2)=0\iff 2x-y+2=0$

2.2 Dạng 2: Sử dụng phép quay để giải các bài toán dựng hình

Phương pháp giải: Xem điểm cần dựng là giao của một đường có sẵn và ảnh của một đường khác qua phép quay $Q_{(I;\alpha )}$ nào đó

Ví dụ 3: Cho hai đường thẳng a, b và điểm C không nằm trên chúng. Hãy tìm trên a và b lần lượt hai điểm A và B sao cho tam giác ABC là tam giác đều

Lời giải

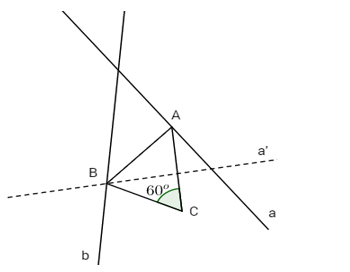
Nếu xem B là ảnh của A qua phép quay tâm C góc quay 60° thì B sẽ là giao của đường thẳng b với đường thẳng a’ là ảnh của a qua phép quay nói trên

Số nghiệm của bài toán là số giao điểm của đường thẳng b với đường thẳng a’

Ví dụ 4: Cho điểm A và hai đường thẳng $d_1,d_2$. Dựng tam giác ABC vuông cân tại A sao cho $B\in d_1,C\in d_2$

Lời giải

- Dựng đường thẳng $d{\text{'}}_2$ là ảnh của $d_2$ qua $Q_{(A;-90°)}$

- Dựng giao điểm $B=d_1\cap d{\text{'}}_2$

- Dựng đường thẳng qua A vuông góc với AB cắt $d_2$ tại C

Tam giác ABC là tam giác cần dựng

Nhận xét:

- Nếu $d_1,d_2$ không vuông góc thì bài toán có một nghiệm hình

- Nếu $d_1\perp d_2$ và A nằm trên đường phân giác của một trong các góc tạo bởi $d_1,d_2$ thì bài toán có vô số nghiệm hình

- Nếu $d_1\perp d_2$ và A không nằm trên đường phân giác của một trong các góc tạo bởi $d_1,d_2$ thì bài toán vô nghiệm hình

2.3 Dạng 3: Sử dụng phép quay để giải các bài toán tập hợp điểm

Phương pháp giải: Xem điểm cần dựng là giao của một đường có sẵn và ảnh của một đường khác qua phép quay $Q_{(I;\alpha )}$ nào đó. Để tìm tập hợp điểm M′ ta đi tìm tập hợp điểm M mà $Q_{(I;\alpha )}$ nào đó biến điểm M thành điểm M′, khi đó nếu $M\in \left(H\right)$ thì $M\text{'}\in \left(H\text{'}\right)=Q_{(I;\alpha )}\left(\left(H\right)\right)$

Ví dụ 5: Cho đường tròn (O, R), A là một điểm cố định không trùng với tâm O, BC là một dây cung của (O), BC di động nhưng số đo của cung BC luôn bằng .Gọi I là trung điểm của BC, vẽ tam giác đều AIJ. Tìm tập hợp điểm J

Lời giải

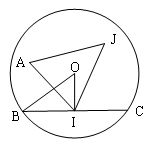
Ta có I là trung điểm của BC và cung $BC=120°$

Nên $OI\perp BC$ và $\widehat{BOI}=60°$

Xét tam giác OIB có:

$OI=OBcos\widehat{BOI}=Rcos60°=\frac{R}{2}$

Do đó tập hợp các điểm I là đường tròn $\left(\gamma \right)$ tâm O bán kính $\frac{R}{2}$

Mặt khác, tam giác AIJ đều nên ta có

$\left\{\begin{array}{l}AJ=AI\\ \left(\overrightarrow{AI};\overrightarrow{AJ}\right)=60°\end{array}\right.\Rightarrow J=Q_A^{60°}\left[\left(\gamma \right)\right]$

Mà tập hợp các điểm I là đường tròn nên tập hợp các điểm J là hai đường tròn $\left({\gamma }_1\right)$ và $\left({\gamma }_2\right)$ với:

$\begin{array}{l}\left({\gamma }_1\right)=Q_A^{60°}\left[\left(\gamma \right)\right]\\ \left({\gamma }_2\right)=Q_A^{60°}\left[\left(\gamma \right)\right]\end{array}$

$\left({\gamma }_1\right)$ là đường tròn tâm $\left(O_1\right)$, bán kính $\frac{R}{2}$ với $O_1=Q_A^{60°}\left(O\right)$

$\left({\gamma }_2\right)$ là đường tròn tâm $\left(O_2\right)$, bán kính $\frac{R}{2}$ với $O_2=Q_A^{-60°}\left(O\right)$

Ví dụ 6: Cho đường thẳng a và một điểm G không nằm trên a. Với mỗi điểm A nằm trên a ta dựng tam giác đều ABC có tâm G. Tìm quỹ tích các điểm B, C khi A di động trên a

Lời giải

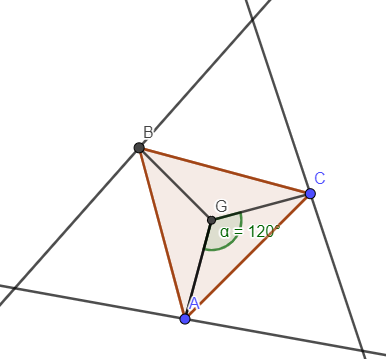
Do tam giác ABC đều và có tâm G nên phép quay tâm G góc quay biến A thành B hoặc C và phép quay tâm G góc quay $240°$biến A thành B hoặc C

Mà $A\in a$ nên B, C thuộc các đường thẳng là ảnh của a trong hai phép quay nói trên

Vậy quỹ tích các điểm B, C là các đường thẳng ảnh của a trong hai phép quay tâm G góc quay $120°$ và $240°$

2.4 Dạng 4: Sử dụng phép quay để giải các bài toán hình học phẳng

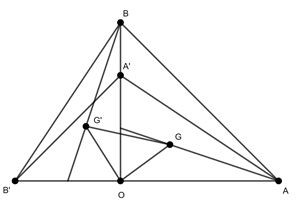
Ví dụ 7: Cho hai tam giác vuông cân OAB và OA'B' có chung đỉnh O sao cho O nằm trên đoạn thẳng AB' và nằm ngoài đoạn thẳng A'B. Gọi G và G' lần lượt là trọng tâm các tam giác OAA' và OBB'. Chứng minh rằng GOG' là tam giác vuông cân

Lời giải

Xét phép quay Q tâm O góc quay $90°$, ta có:

$\begin{array}{l}\Delta OBB\text{'}=Q_O^{90°}(△OAA\text{'})\Rightarrow G\text{'}=Q_O^{90°}\left(G\right)\\ \Rightarrow \widehat{GOG\text{'}}=90°,OG\text{'}=OG\end{array}$

Vậy, ta được tam giác GOG' là tam giác vuông cân

Ví dụ 8: Cho tam giác ABC, dựng ở ngoài tam giác ấy hai hình vuông ABDE và BCKF. Gọi P là trung điểm cạnh AC, H là điểm đối xứng của D qua B, M là trung điểm đoạn FH

a. Xác định ảnh của hai vectơ $\overrightarrow{BA}$ và $\overrightarrow{BP}$ trong phép quay tâm B góc $90°$

b. Chứng minh rằng DF = 2BP và DF vuông góc với BP

Lời giải

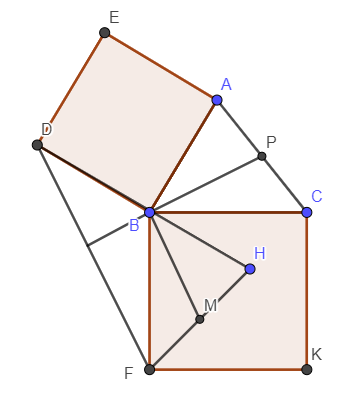
a. Ta có: $\left\{\begin{array}{l}BA=BH(=BD)\\ (\overrightarrow{BA};\overrightarrow{BH})=90°\end{array}\right.$

$\Rightarrow Q_B^{90°}\left(A\right)=H;Q_B^{90°}\left(\overrightarrow{BA}\right)=\overrightarrow{BH}$

$$\begin{gathered} Q_B^{90°}\left(A\right)=H;Q_B^{90°}\left(C\right)=F \\ \Rightarrow Q_B^{90°}\left(\overrightarrow{AC}\right)=\overrightarrow{HF} \end{gathered}$$

b. Vì P là trung điểm của AC nên theo tính chất của phép quay ta có ảnh của P qua phép quay trên trung điểm M của HF

$Q_B^{90°}\left(\overrightarrow{BP}\right)=\overrightarrow{BM}\Rightarrow \left\{\begin{array}{l}BP=BM\\ BP\perp BM\end{array}\right.$

Mặt khác: $BM=\frac{1}{2}DE,BM//DF$

$\Rightarrow BP=\frac{1}{2}DF;DF\perp BP$

III. Bài tập áp dụng

Bài 1: Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ta dựng các hình vuông ABDE và ACFH. Gọi I là trung điểm của cạnh BCE

a. Chứng minh rằng AE = CD

b. Gọi I, J lần lượt là trung điểm của AE và CD. Chứng minh rằng tam giác BIJ là một tam giác đều

Bài 2: Cho nửa đường tròn tâm O đường kính BC. Điểm A chạy trên nửa đường tròn đó. Dựng về phía ngoài của tam giác ABC hình vuông ABEF. Chứng minh rằng E chạy trên một nửa đường tròn cố định

Bài 3: Trong mặt phẳng toạ độ Oxy cho điểm A (3; 4). Hãy tìm toạ độ điểm A’ là ảnh của A qua phép quay tâm O góc $90°$

Bài 4: Cho hình vuông ABCD tâm O. M là trung điểm của AB, N là trung điểm của OA. Tìm ảnh của tam giác AMN qua phép quay tâm O góc $90°$

Bài 5: Cho tam giác ABC. Dựng về phía ngoài của tam giác các hình vuông BCIJ, ACMN, ABEF và gọi O, P, Q lần lượt là tâm đối xứng của chúng

a. Gọi D là trung điểm của AB. Chứng minh rằng DOP là tam giác vuông cân đỉnh D

b. Chứng minh AO vuông góc với PQ và AO = PQ

Bài 6: Dựng tam giác đều biết ba đỉnh nằm trên bốn cạnh của một hình bình hành cho trước

Bài 7: Trong mặt phẳng Oxy, cho điểm B (-3; 6). Tìm tọa độ điểm E sao cho B là ảnh của E qua phép quay tâm O góc quay -$90°$

Bài 8: Cho hình vuông tâm O. Hỏi có bao nhiêu phép quay tâm O góc quay $\alpha$, $0<\alpha \le 2\pi$ biến hình vuông trên thành chính nó?

A. 1

B. 2

C. 3

D. 4

Bài 9: Trong mặt phẳng với hệ trục tọa độ Oxy, cho điểm M (2; 0) và điểm N (0; 2). Phép quay tâm O biến điểm M thành điển N, khi đó góc quay của nó là bao nhiêu?Bài 10: Trong mặt phẳng Oxy cho điểm A (3; 0). Tìm tọa độ ảnh A¢ của điểm A qua phép quay $Q_O^{90°}$