100 công thức về tính thể tích khối lăng trụ (2024 có đáp án) và cách giải các dạng toán

Công thức tính thể tích khối lăng trụ đầy đủ, chi tiết nhất 

1. Lí thuyết

a. Định nghĩa: Một đa giác có hai mặt đáy song song và bằng nhau, mặt bên là hình bình hành thì đa giác đó gọi là hình lăng trụ.

b. Các tính chất hình lăng trụ:

- Các cạnh bên song song và bằng nhau

- Các mặt bên là hình bình hành

- Hai đáy của lăng trụ là hai đa giác bằng nhau và nằm trong 2 mặt phẳng song song với nhau

c. Một số loại lăng trụ thường gặp

- Lăng trụ xiên: Giống với tính chất của hình lăng trụ thông thường

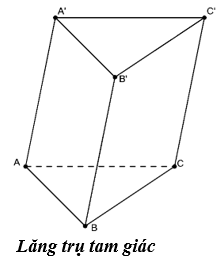
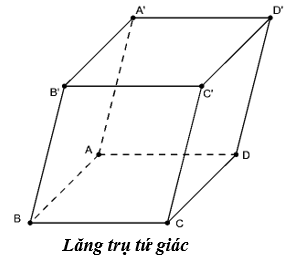
- Lăng trụ đứng:

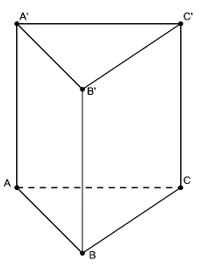
+ Các cạnh bên vuông góc với đáy.

+ Các cạnh bên chính là đường cao của nó

+ Các mặt bên là hình chữ nhật

- Lăng trụ đều:

+ Là lăng trụ đứng có đáy là đa giác đều

+ Các mặt bên là các hình chữ nhật bằng nhau

- Hình hộp: Là lăng trụ có đáy là hình bình hành

+ Hình hộp đứng có các cạnh bên vuông góc với đáy

+ Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật

+ Hình lập phương là hình hộp đứng có tất cả các cạnh bằng nhau.

2. Công thức tính thể tích khối lăng trụ

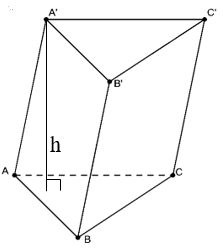
- Cho khối lăng trụ có:

+ Chiều cao là h

+ Diện tích đáy là S

Khi đó thể tích: V=h.S

- Thể tích của hình hộp chữ nhật có:

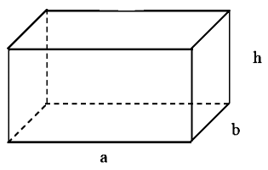
+ Chiều dài a

+ Chiều rộng b

+ Chiều cao h là:

V=a.b.h

- Thể tích hình lập phương cạnh a là $V=a^3$

3. Các dạng toán tính thể tích khối lăng trụ

Dạng 1. Tính thể tích khối lăng trụ đứng

VD1. Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân tại B. Biết $AC=a\sqrt{2}$ và $BC\text{'}=2a$. Tính thể tích khối lăng trụ ABC.A’B’C’
Lời giải:

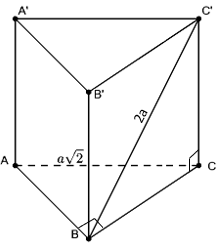
Ta có $\Delta ABC$ vuông cân tại B nên $AB=BC=a$

ABC.A’B’C’ là lăng trụ đứng nên $C\text{'}C\perp BC$. Do đó $\Delta BCC\text{'}$ vuông tại C

Áp dụng định lí Pytago ta được: $CC\text{'}=a\sqrt{3}$

Diện tích $\Delta ABC$ bằng $\frac{1}{2}{a}^2$

Suy ra :

$$\begin{gathered} V_{ABC.A\text{'}B\text{'}C\text{'}}=CC\text{'}.S_{\Delta ABC} \\ =\frac{a^3\sqrt{3}}{2} \end{gathered}$$

VD2. Cho lăng trụ đều ABC.A’B’C’ cạnh a. Góc giữa A’B với đáy bằng ${60}^{\circ }$. Tính thể tích khối lăng trụ.

Lời giải:

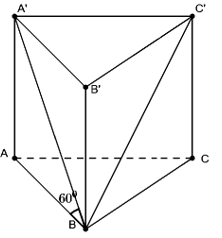
Do ABC.A’B’C’ là lăng trụ đều nên $A\text{'}A\perp \left(ABC\right)$ và ABC là tam giác đều

Ta có :

$$\begin{gathered} \left(A\text{'}B,\left(ABC\right)\right)=\left(A\text{'}B,AB\right)=\widehat{A\text{'}BA}={60}^{\circ } \\ \Rightarrow A\text{}\text{'}A=AB.\tan {60}^{\circ }=a\sqrt{3} \end{gathered}$$

Diện tích tam giác đều ABC là $S_{\Delta ABC}=\frac{a^2\sqrt{3}}{4}$

Do đó thể tích lăng trụ là :

$$\begin{gathered} V=A\text{'}A.S_{\Delta ABC} \\ =a\sqrt{3}.\frac{a^2\sqrt{3}}{4}=\frac{3a^3}{4} \end{gathered}$$

Dạng 2. Tính thể tích của khối lăng trụ xiên

VD1. Cho lăng trụ xiên ABC.A’B’C’ có đáy là tam giác đều cạnh a. Cạnh bên bằng $a\sqrt{3}$ và hợp với đáy một góc bằng ${45}^{\circ }$. Thể tích của lăng trụ bằng?

Lời giải:

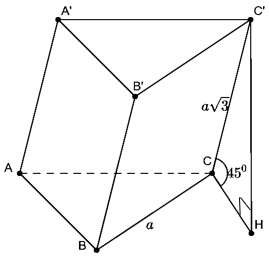
Gọi hình chiếu vuông góc của C’ xuông (ABC) là H.

Khi đó :

$$\begin{gathered} \left(C\text{'}C,\left(ABC\right)\right)=\left(C\text{'}C,HC\right) \\ =\widehat{C\text{'}CH}={45}^{\circ } \\ \Rightarrow C\text{'}H=C\text{'}C.\sin {45}^{\circ }=\frac{a\sqrt{6}}{2} \end{gathered}$$

Diện tích tam giác ABC là $S_{\Delta ABC}=\frac{a^2\sqrt{3}}{4}$

Suy ra thể tích lăng trụ là :

$$\begin{gathered} V=C\text{'}H.S_{\Delta ABC} \\ =\frac{a\sqrt{6}}{2}\frac{a^2\sqrt{3}}{4}=\frac{3a^3\sqrt{2}}{8} \end{gathered}$$

VD2. Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của A’ xuống (ABC) là trung điểm H của AB. Mặt bên (ACC’A’) tạo với đáy góc ${60}^{\circ }$ Tính thể tích khối lăng trụ ABC.A’B’C’

Lời giải:

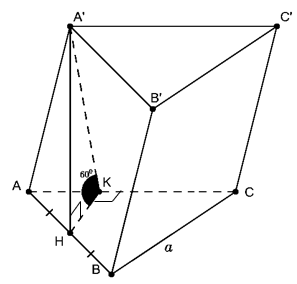
Trong (ABC) kẻ $HK\perp AC$

Ta có:

$\left\{\begin{array}{l}AC\perp HK\\ AC\perp A\text{'}H\end{array}\right.\Rightarrow AC\perp A\text{'}K$

Khi đó góc giữa (ABC) và (ACC’A’) là góc giữa HK và A’K là $\widehat{A\text{'}KH}={60}^{\circ }$

Xét tam giác AHK vuông tại K có $\widehat{A}={60}^{\circ }$,

$$\begin{gathered} AH=\frac{a}{2} \\ \Rightarrow HK=AH.\sin {60}^{\circ }=\frac{a\sqrt{3}}{4} \end{gathered}$$

Xét tam giác A’HK vuông tại H có $\widehat{K}={60}^{\circ }$

$\Rightarrow A\text{'}H=HK.\tan {60}^{\circ }=\frac{3a}{4}$

Diện tích tam giác ABC là $S_{\Delta ABC}=\frac{a^2\sqrt{3}}{4}$

Suy ra thể tích lăng trụ là :

$$\begin{gathered} V=A\text{'}H.S_{\Delta ABC} \\ =\frac{3a}{4}\frac{a^2\sqrt{3}}{4}=\frac{3a^3\sqrt{3}}{16} \end{gathered}$$

4. Luyện tập

Bài 1. Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông tại A; $AB=a, AC=2a\sqrt{2}$. Khoảng cách từ A đến mp (A’BC) bằng $\frac{a\sqrt{3}}{2}$. Tính thể tích khối lăng trụ đã cho.

Bài 2. Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thoi cạnh a. $\widehat{BAD}={60}^{\circ }$$AC\text{'}=2a$. Tính thể tích lăng trụ ABCD.A’B’C’D’.

Bài 3. Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B; $AB=a$. Hình chiếu của A’ lên (ABC) là điểm H thuộc cạnh AC sao cho $HC=2HA$. Mặt bên $\left(ABB\text{'}A\text{'}\right)$ tạo với đáy góc ${60}^{\circ }$. Tính thể tích khối lăng trụ ABC.A’B’C’.

Bài 4. Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh a. Cạnh bên AA’ = a. Hình chiếu của A’ trên mp (ABCD) trùng với trung điểm I của cạnh AB. Gọi K là trung điểm BC. Tính thể tích khối chóp A’.IKD

Bài 5. Cho lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a. Hình chiếu H của A’ lên mp (ABC) trùng với trung điểm của BC. Góc giữa mp (A’ABB’) và đáy bằng ${60}^{\circ }$. Tính thể tích khối tứ diện ABCA’.