100 bài tập về Biện luận số nghiệm của phương trình dựa vào đồ thị hàm số (có đáp án 2024)

Biện luận số nghiệm của phương trình dựa vào đồ thị hàm số

A. PHƯƠNG PHÁP GIẢI.

Đưa phương trình g(x;m) = 0 về các dạng bài sau:

Dạng 1: f(x) = h(m), trong đó h(m) là một hàm phụ thuộc vào tham số m.

- Vẽ đồ thị hàm số y = f(x), tìm các giá trị cực đại, cực tiểu, giá trị của hàm số tại các điểm đầu mút của miền xác định của hàm số y = f(x).

- Đường thẳng y = h(m) di động song song với trục hoành, dựa vào số giao điểm của đường thẳng y = h(m) với đồ thị hàm số y = f(x) để biện luận số nghiệm của phương trình g(x;m) = 0.

Dạng 2: $f\left(x\right)=ax+b$, trong đó a cố định, b thay đổi.

- Vẽ đồ thị hàm số y = f(x).

- Tìm các tiếp tuyến với đồ thị hàm số y = f(x) có hệ số góc cho trước là a.

- Tìm giao điểm của tiếp tuyến với trục tung ( hoặc trục hoành) và giao điểm của đường thẳng $y=ax+b$ với trục tung ( hoặc trục hoành). Cho b di động trên trục tung để suy ra số nghiệm của phương trình g(x;m).

Dạng 3: $f\left(x\right)=ax+b$, trong đó a thay đổi, b tùy ý.

- Vẽ đồ thị hàm số y = f(x).

- Tìm điểm A(x0,y0) là điểm cố định của đường thẳng $y=ax+b$.

- Viết các phương trình tiếp tuyến với đồ thị hàm số y = f(x) đi qua A.

- Cho đường thẳng $y=ax+b$ xoay quanh điểm cố định A. Từ đó suy ra nghiệm của phương trình g(x;m) = 0.

Chú ý:

- Nếu hàm số y = f(x) có miền xác định là đoạn thẳng [a,b] thì đồ thị hàm số y =f(x) ta chỉ xét phần x [a,b].

- Một số bài toán đặt ẩn phụ t = $\partial \left(x\right)$, với $\partial \left(x\right)$ là một biểu thức trong phương trình ban đầu thì:

+ Dựa vào miền xác định của x để tìm miền xác định của t.

+ Vẽ đồ thị hàm số y = f(t) rồi làm giống như trên.

- Đồ thị hàm số chứa giá trị tuyệt đối.

1. Dạng y = |f(x)|.

+ Vẽ đồ thị ( C) của hàm số y = f(x).

+ Lấy các phần của ( C) ở phía trên trục hoành.

+ Lấy thêm phần đối xứng qua trục hoành của các phần của ( C) phía dưới trục hoành.

2. Dạng $y=\frac{f\left(x\right)}{\left|g\left(x\right)\right|}$

+ Vẽ đồ thị ( C) của hàm số y = f(x).

+ Lấy các phần của ( C) tương ứng với x sao cho g(x) >0.

+ Lấy thêm phần đối xứng qua trục hoành của các phần của ( C) tương ứng với x sao cho g(x) <0.

3. Dạng $y=\frac{\left|f\left(x\right)\right|}{g\left(x\right)}$ làm tương tự như mục 2.

4. Dạng y = f(x) + |g(x)|.

Đồ thị gồm 2 phần:

+ Đồ thị ( C) y= f(x) + g(x) tương ứng với x sao cho g(x) >0.

+ Đồ thị ( C’) y = f(x) – g(x) tương ứng với x sao cho g(x) <0.

5. Dạng y = f(|x|).

+ Vẽ đồ thị ( C) của hàm số y= f(x).

+ Lấy phần của ( C) bên phải trục oy tương ứng với x>0.

+ Lấy thêm phần đối xứng qua trục oy của phần của ( C) bên phải trục oy.

Mở rộng: Đối với bài toán bất phương trình làm tương tự, lưu ý:

Giả sử hàm f(x) tồn tại Max-Min trên R. Ta có:

$$\begin{gathered} m\ge f\left(x\right),\forall x\in ℝ\iff m\ge \underset{ℝ}{Max}f\left(x\right) \\ m\le f\left(x\right),\forall x\in ℝ\iff m\le \underset{ℝ}{Min}f\left(x\right) \\ m>f\left(x\right),\forall x\in ℝ\iff m>\underset{ℝ}{Max}f\left(x\right) \\ m<f\left(x\right),\forall x\in ℝ\iff m<\underset{ℝ}{Min}f\left(x\right) \end{gathered}$$

- Nếu hàm f(x) không tồn tại Max-Min trên R, tuy nhiên thông qua bảng biến thiên ta tìm được điều kiện bị chặn: $M_1<f\left(x\right)<M_2$, khi đó:

$$\begin{gathered} m\ge f\left(x\right),\forall x\in ℝ\iff m\ge M_2 \\ m\le f\left(x\right),\forall x\in ℝ\iff m\le M_1 \\ m>f\left(x\right),\forall x\in ℝ\iff m\ge M_2 \\ m<f\left(x\right),\forall x\in ℝ\iff m\le M_1 \end{gathered}$$

Mở rộng: Đối với dạng bài tập phương trình tương giao.

- Cách giải: Chuyển tất cả ẩn, tham số của phương trình về 1 vế, ta sẽ được phương trình mới có dạng: g(x;m) = 0.

Như vậy, bài toán đã được đưa về dạng cơ bản. Tuỳ từng phương trình, chọn cách giải thích hợp.

B. VÍ DỤ MINH HOẠ.

Ví dụ 1. Cho hàm số $y=f\left(x\right)=x^4-2x^2+2$ có bảng biến thiên như sau

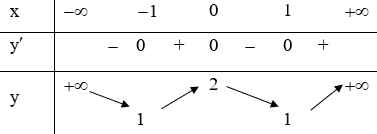
Số giá trị nguyên dương của m để phương trình $2x^4-4x^2+m-5=0$ có đúng 2 nghiệm

A. 3

B. 4

C. 5

D. 6

Lời giải

Ta có: PT đã cho:

$$\begin{gathered} \iff x^4-2x^2=\frac{5-m}{2} \\ \iff x^4-2x^2+2=\frac{9-m}{2}\left(2\right) \end{gathered}$$

Số nghiệm của phương trình (2) là số giao điểm của đồ thị (C) và đường thẳng $y=\frac{9-m}{2}$

Do vậy phương trình đã cho có 2 nghiệm $\iff \left(d\right)$ cắt (C) tại 2 điểm phân biệt

$\iff \left[\begin{array}{l}\frac{9-m}{2}=1\\ \frac{9-m}{2}>2\end{array}\right.\iff \left[\begin{array}{l}m=7\\ m<5\end{array}\right.$

Kết hợp:

$m\in {\mathbb{Z}}^{+}\Rightarrow m=\left\{1;2;3;4;7\right\}$

Vậy có 5 giá trị của m thỏa mãn yêu cầu bài toán.

Chọn C.

Ví dụ 2. Cho hàm số $y=2x^3-3x^2+1$ có đồ thị (C). Biện luận theo m số nghiệm phương trình $2x^3-3x^2-m-1=0$ (*)

Lời giải

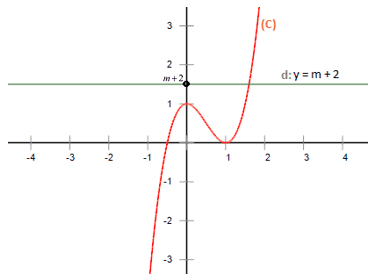
Đồ thị (C)

Ta có:

$$\begin{gathered} 2x^3-3x^2-m-1=0 \\ \iff 2x^3-3x^2+1=m+2 \end{gathered}$$

Vậy số nghiệm của phương trình (*) bằng số điểm chung giữa đồ thị (C) và đường thẳng d: $y=m+2$.

- Với $m+2<0$ hoặc $m+2>1\iff m<-2$ hoặc $m>-1$ thì d và (C) có một điểm chung $\Rightarrow$ phương trình (*) có một nghiệm.

- Với $m+2=0$ hoặc $m+2=1\iff$m = –2 hoặc m = –1 thì d và (C) có hai điểm chung $\Rightarrow$ phương trình (*) có hai nghiệm.

- Với $0<m+2<1$$\iff -2<m<-1$thì d và (C) có ba điểm chung $\Rightarrow$ phương trình (*) có ba nghiệm.

Ví dụ 3. Cho hàm số $y=x^4-4x^2+3$ có đồ thị (C). Tìm m để phương trình $-x^4+4x^2-3-m=0$ (*) có 4 nghiệm phân biệt.

Lời giải

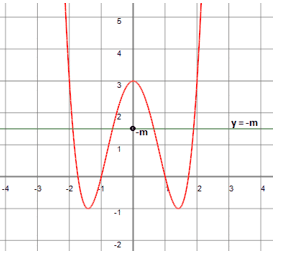
Đồ thị (C)

Ta có: (*) $x^4-4x^2+3=-m$

Số nghiệm của phương trình (*) bằng số điểm chung giữa đồ thị (C) và đường thẳng d: $y=-m$.

Vậy để phương trình (*) có 4 nghiệm phân biệt thì d và (C) phải cắt nhau tại 4 điểm.

$\Rightarrow -1<-m<3$

$\iff -3<m<1$

Vậy với $-3<m<1$ thì phương trình (*) có 4 nghiệm phân biệt.

C. BÀI TẬP VẬN DỤNG.

Câu 1. (Cho hàm số bậc bốn $y=f\left(x\right)$ có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình $f\left(x\right)=\frac{1}{2}$ là

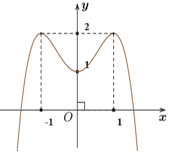
A. 2.

B. 4.

C. 1

D. 3.

Câu 2. Cho hàm số bậc ba $y=f\left(x\right)$ có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình $f\left(x\right)=1$ là:

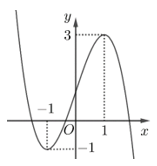
A. 0.

B. 3.

C. 1.

D. 2.

Câu 3. Cho hàm số bậc ba $y=f\left(x\right)$ có đồ thị là đường cong trong hình vẽ bên.

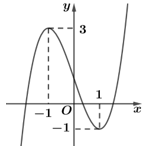
Số nghiệm thực của phương trình $f\left(x\right)=2$ là:

A. 0

B. 3

C. 1

D. 2

Câu 4. Cho hàm số y = f(x) xác định trên $R\backslash \left\{0\right\}$ , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau.

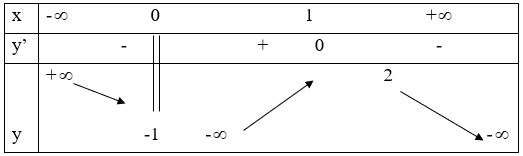
Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình $f\left(x\right)=m$ có ba nghiệm phân biệt.

A. [-1;2].

B. (-1;2).

C. (-1;2].

D. (- ;2].

Câu 5. Cho hàm số $f\left(x\right)$ có bảng biến thiên như sau:

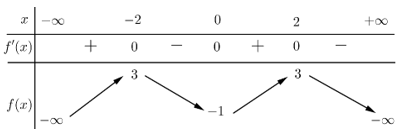
Số nghiệm thực của phương trình $2f\left(x\right)-3=0$ là:

A. 2.

B. 1.

C. 4.

D. 3.

Câu 6. Cho hàm số $f\left(x\right)$ có bảng biến thiên như sau:

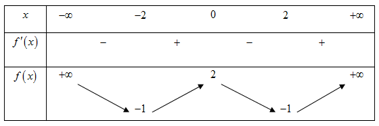
Số nghiệm thực của phương trình $3f\left(x\right)-5=0$ là:

A. 2

B. 3

C. 4

D. 0

Câu 7. Cho hàm số $y=-x^4+2x^2$ có đồ thị như hình bên.

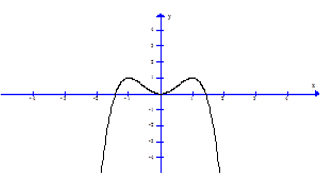
Tìm tất cả các giá trị thực của tham số m để phương trình $-x^4+2x^2=m$ có bốn nghiệm thực phân biệt.

A. m > 0.

B. $0\le m\le 1$ .

C. $0<m<1$ .

D. m<1.

Câu 8. Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ.

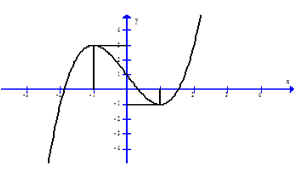
Tìm tất cả các giá trị m để phương trình $f\left(\sin x\right)=0$ có nghiệm thực thuộc khoảng (0;π).

A. [-1;3).

B. (-1; 1).

C. (-1;3).

D. [-1;1).

Câu 9. Cho hàm số $f\left(x\right)$, hàm số $y=f^{\text{'}}\left(x\right)$ liên tục trên R và có đồ thị như hình vẽ bên.

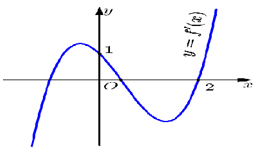
Bất phương trình $f\left(x\right)<x+m$ ( m là tham số thực) nghiệm đúng với mọi $x\in \left(0;2\right)$ khi và chỉ khi:

A. $m\ge f\left(2\right)-2$

B. $m\ge f\left(0\right)$

C. $m>f\left(2\right)-2$

D. $m>f\left(0\right)$ .

Câu 10. Cho hàm số f(x) , hàm số y = f’(x) liên tục trên R và có đồ thị như hình vẽ bên.

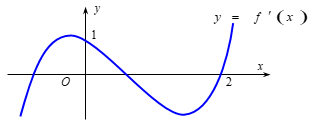
Bất phương trình $f\left(x\right)>x+m$ (m là tham số thực) nghiệm đúng với mọi $x\in (0;2)$ khi và chỉ khi:

A. $m\le f\left(2\right)-2$ .

B. $m<f\left(2\right)-2$ .

C. $m\le f\left(0\right)$.

D. $m<f\left(0\right).$

Câu 11. Cho hàm số bậc ba $y=f\left(x\right)$ có đồ thị như hình vẽ bên.

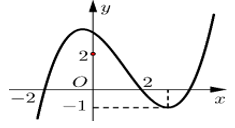
Số nghiệm thực của phương trình $\left|f\left(x^3-3x\right)\right|=\frac{4}{3}$ là

A. 3

B. 8

C. 7

D. 4

Câu 12. Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên.

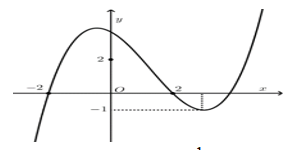
Số nghiệm thực của phương trình $\left|f\right(x^3-3x\left)\right|=\frac{1}{2}$ là:

A. 6.

B. 10.

C. 12.

D. 3.

Câu 13. Cho hàm số y = f(x). Hàm số y = f’(x) có bảng biến thiên như hình vẽ sau

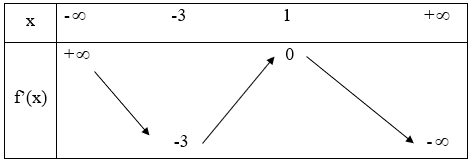
Bất phương trình $f\left(x\right)<e^x+m$ đúng với mọi $x\in (-1;1)$ khi và chỉ khi

A. $m\ge f\left(1\right)-e$

B. $m>f(-1)-\frac{1}{e}$

C. $m\ge f(-1)-\frac{1}{e}$

D. $m>f\left(1\right)-e$

Câu 14 Cho hàm số $f\left(x\right)=m{x}^4+n{x}^3+p{x}^2+qx+r$$(m,n,p,q,r\in R)$.

Hàm số f’(x) có đồ thị như hình vẽ.

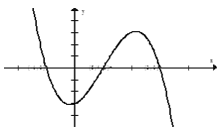
Tập nghiệm của phương trình f(x) = r có số phần tử là:

A. 4.

B. 3.

C. 1.

D. 2.

Câu 15. Cho hàm số bậc bốn $y=f\left(x\right)$ có đồ thị là đường cong trong hình vẽ bên.

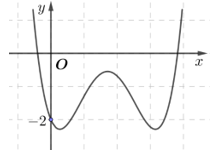
Số nghiệm thực phân biệt của phương trình $f\left(x^{2}f\left(x\right)\right)+2=0$ là

A. 8

B. 12

C. 6

D. 9

Câu 16. Cho hàm số $y=f\left(x\right)$ có đồ thị là đường cong trong hình vẽ bên.

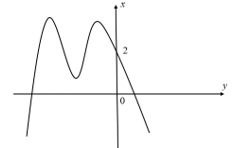
Số nghiệm thực của phương trình $f\left(x^{2}f\left(x\right)\right)=2$ là:

A. 6.

B. 12.

C. 8.

D. 9.

Đáp án