100 công thức về khai triển nhị thức Niu-tơn chi tiết nhất (2024 có đáp án) và cách giải các dạng toán

Công thức khai triển nhị thức Niu – tơn 

1. Tổng hợp lý thuyết

a) Định nghĩa:

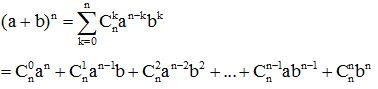
b) Nhận xét:

Trong khai triển Niu - tơn (a + b)n có các tính chất sau

- Gồm có n + 1 số hạng

- Số mũ của a giảm từ n đến 0 và số mũ của b tăng từ 0 đến n

- Tổng các số mũ của a và b trong mỗi số hạng bằng n

- Các hệ số có tính đối xứng: $C_n^k=C_n^{n-k}$

- Quan hệ giữa hai hệ số liên tiếp: $C_n^k+C_n^{k+1}=C_{n+1}^{k+1}$

- Số hạng thứ k + 1 của khai triển: $T_{k+1}=C_n^k{a}^{n-k}{b}^k$

Ví dụ:

Số hạng thứ nhất $T_1=T_{0+1}=C_n^0{a}^n$, số hạng thứ k: $T_k=T_{(k-1)+1}=C_n^{k-1}{a}^{n-k+1}{b}^{k-1}$

c) Hệ quả:

Ta có: ${(1+x)}^n=C_n^0+x{C}_n^1+x^2{C}_n^2+\mathrm{...}+x^n{C}_n^n$

Từ khai triển này ta có các kết quả sau

$\begin{array}{l}{C}_n^0+C_n^1+\mathrm{...}+C_n^n=2^n\\ C_n^0-C_n^1+C_n^2-\mathrm{...}+{\left(-1\right)}^n{C}_n^n=0\end{array}$

2. Công thức tính

Công thức khai triển nhị thức Niu – tơn:

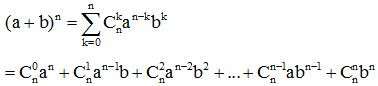
3. Ví dụ minh họa

Ví dụ 1: Khai triển (1 – 3x)6 thành tổng các đơn thức.

Lời giải

Áp dụng công thức khai triển nhị thức Niu – tơn:

(1 – 3x)6

$=C_6^0{.1}^6+C_6^1{.1}^5{\left(-3x\right)}^1+C_6^2{.1}^4{\left(-3x\right)}^2$$+C_6^3{.1}^3{\left(-3x\right)}^3+C_6^4{.1}^2{\left(-3x\right)}^4$$+C_6^5{.1}^1{\left(-3x\right)}^5+C_6^6{\left(-3x\right)}^6$

= 1 – 18x + 135x2 – 540x3 + 1215x4 – 1458x5 + 729x6.

Ví dụ 2: Khai triển (x + 2y)5 thành tổng các đơn thức.

Lời giải

Áp dụng công thức khai triển nhị thức Niu – tơn:

(x + 2y)5

$=C_5^0{x}^5+C_5^1{x}^4\left(2y\right)+C_5^2{x}^3{\left(2y\right)}^2$$+C_5^3{x}^2{\left(2y\right)}^3+C_5^{4}x{\left(2y\right)}^4+C_5^5{\left(2y\right)}^5$

= x5 + 10x4y + 40x3y2 + 80x2y3 + 80xy4 + 32y5.