100 bài tập về các phương pháp tính tích phân (2024 có đáp án) và cách giải các dạng toán

Các phương pháp tính tích phân và cách giải 

A. LÝ THUYẾT

1. Phương pháp đổi biến số.

1.1 Định lý 1

Cho hàm số f(x) liên tục trên đoạn $\left[a;b\right]$. Giả sử hàm số $x=\phi \left(t\right)$ có đạo hàm liên tục trên đoạn $\left[\alpha ;\beta \right]$ sao cho $\phi \left(\alpha \right)=a;\phi \left(b\right)=b$ và $a\le \phi \left(t\right)\le b$ với mọi $t\in \left[\alpha ;\beta \right]$. Khi đó:

$\underset{a}{\overset{b}{\int }}f\left(x\right)dx=\underset{\alpha }{\overset{\beta }{\int }}f\left(\phi \left(t\right)\right)\phi \text{'}\left(t\right)dt$

Từ định lý 1 ta rút ra các bước đổi biến số

+ Bước 1 : Đặt $x=\phi \left(t\right)$, ta xác định đoạn $\left[\alpha ;\beta \right]$ sao cho $\phi \left(\alpha \right)=a,\phi \left(\beta \right)=b$ và $a\le \phi \left(t\right)\le b$, $\forall t\in \left[\alpha ;\beta \right]$;

+ Bước 2 : Biến đổi : $f\left(x\right)dx=f\left(\phi \left(t\right)\right)\phi \text{'}\left(t\right)dt=g\left(t\right)dt$

+ Bước 3 : Tìm một nguyên hàm G(t) của g(t)

+ Bước 4 : Tính $\underset{\alpha }{\overset{\beta }{\int }}g\left(t\right)dt=G\left(\beta \right)-G\left(\alpha \right)$

+ BƯớc 5 : Kết luận $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=G\left(\beta \right)-G\left(\alpha \right)$

1.2 Định lý 2

Cho hàm số $f\left(x\right)$ liên tục trên đoạn $\left[a;b\right]$. Nếu hàm số $u=u\left(x\right)$ có đạo hàm liên tục trên đoạn $\left[a;b\right]$ và $\alpha \le u\left(x\right)\le \beta$ với mọi $x\in \left[a;b\right]$ sao cho $f\left(x\right)=g\left(u\left(x\right)\right)u\text{'}\left(x\right),g\left(u\right)$ liên tục trên đoạn $\left[\alpha ;\beta \right]$ thì $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=\underset{u\left(a\right)}{\overset{u\left(b\right)}{\int }}g\left(u\right)du$

Từ định lý 2 ta rút ra các bước đổi biến số

+ Bước 1 : Đặt $u=u\left(x\right)$,

+ Bước 2 : Biến đổi $f\left(x\right)dx=g\left(u\right)du$.

+ Bước 3 : Tìm một nguyên hàm G(u) của g(u).

+ Bước 4 : Tính $\underset{u\left(a\right)}{\overset{u\left(b\right)}{\int }}g\left(u\right)du=G\left(u\left(b\right)\right)-G\left(u\left(a\right)\right)$.

+ Bước 5 : Kết luận $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=G\left(u\left(b\right)\right)-G\left(u\left(a\right)\right)$

2. Phương pháp tích phân từng phần.

Tương tự tính nguyên hàm từng phần, ta có định lý sau:

Nếu $u=u\left(x\right)$ và $v=v\left(x\right)$ là hai hàm số có đạo hàm liên tục trên đoạn $\left[a;b\right]$ thì

$\underset{a}{\overset{b}{\int }}u\left(x\right)v\text{'}\left(x\right)dx={\left.\left(u\left(x\right)v\left(x\right)\right)\right|}_a^b-\underset{a}{\overset{b}{\int }}u\text{'}\left(x\right)v\left(x\right)dx$ hay $\underset{a}{\overset{b}{\int }}udv={\left.uv\right|}_a^b-\underset{a}{\overset{b}{\int }}vdu$

Hay $\underset{a}{\overset{b}{\int }}udv={\left.uv\right|}_a^b-\underset{a}{\overset{b}{\int }}vdu$.

Một số cách đặt tích phân từng phần thường gặp với: $\underset{a}{\overset{b}{\int }}p\left(x\right)q\left(x\right)dx$

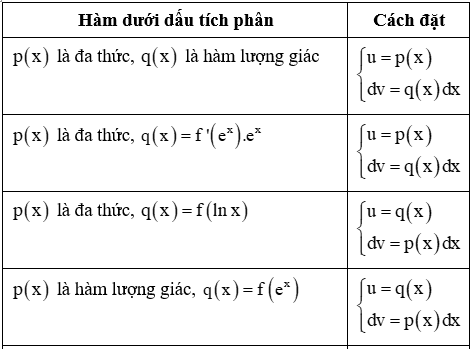
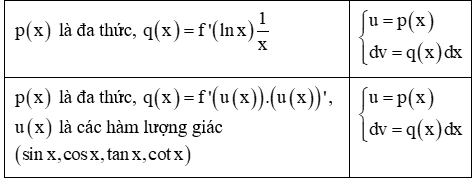
B. CÁC DẠNG TOÁN VÀ VÍ DỤ MINH HOẠ

1. Phương pháp đổi biến số

Dạng 1: Đổi biến số với các hàm vô tỉ quen thuộc

Phương pháp giải: Thực hiện theo các bước ở lý thuyết.

Chú ý:

Trong biểu thức của f(x)dx có chứa căn thì đặt căn đó bằng t.

Trong biểu thức của f(x)dx có chứa biểu thức lũy thừa bậc cao thì đặt biểu thức đó bằng t.

Trong biểu thức của f(x)dx có chứa hàm mũ với biểu thức trên mũ là một hàm số thì đặt biểu thức trên mũ bằng t.

Ví dụ minh họa:

Ví dụ 1: Tính các tích phân sau bằng phương pháp đổi biến số:

a) $I=\underset{0}{\overset{4}{\int }}\frac{dx}{3+\sqrt{2x+1}}.$

b) $I=\underset{0}{\overset{\ln 3}{\int }}\frac{dx}{\sqrt{e^x+1}}.$

Lời giải

Chú ý: Đổi biến nhớ phải đổi cận.

a) Đặt

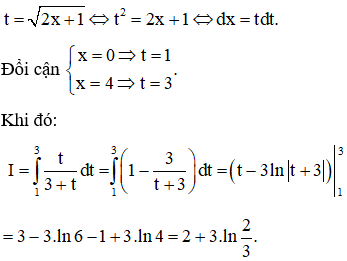
b) Đặt

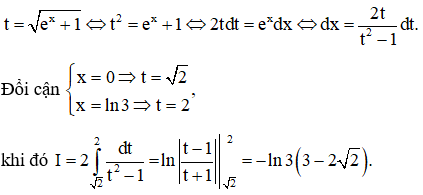
Dạng 2: Tích phân đổi biến số với hàm ẩn

Phương pháp giải: Thực hiện theo các bước ở lý thuyết.

Chú ý tính chất: $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=\underset{a}{\overset{b}{\int }}f\left(t\right)dt=\underset{a}{\overset{b}{\int }}f\left(u\right)du$ (tích phân không phụ thuộc vào biến).

Ví dụ minh họa:

Ví dụ 2: Cho hàm số f(x) liên tục trên R thỏa mãn $\underset{0}{\overset{6}{\int }}f\left(x\right)dx=12.$

Tính tích phân $I=\underset{0}{\overset{2}{\int }}f\left(3x\right)dx.$

A. I = 6

B. I = 36

C. I = 2

D. I = 4

Lời giải

Dạng 3: Tích phân đổi biến số với hàm số chẵn, hàm số lẻ

Bài toán tổng quát: Giả sử hàm số f(x) liên tục trên đoạn [-a; a]. Chứng minh rằng:

a) $\underset{-a}{\overset{a}{\int }}f\left(x\right)dx=2\underset{0}{\overset{a}{\int }}f\left(x\right)dx$ nếu f(x) là hàm số chẵn.

b) $\underset{-a}{\overset{a}{\int }}f\left(x\right)dx=0$ nếu f(x) là hàm số lẻ.

Phương pháp giải

a) Hàm số f(x) là hàm chẵn thì $f\left(-x\right)=f\left(x\right)$

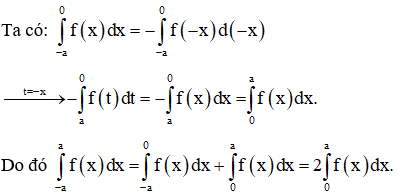
b) Hàm số f(x) là hàm lẻ thì $f\left(-x\right)=-f\left(x\right)$

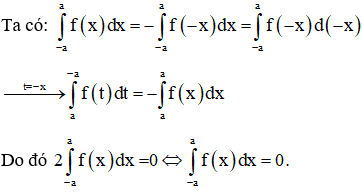
Ví dụ minh họa

Ví dụ 3: Cho hàm số y = f(x) liên tục trên đoạn [0; 1] thỏa mãn $f\left(x\right)+2f\left(1-x\right)=3x,\forall x\in ℝ.$

Tính tích phân $I=\underset{0}{\overset{1}{\int }}f\left(x\right)dx.$

A. $I=\frac{3}{2}.$

B. I = 1.

C. $I=\frac{1}{2}.$

D. I = 2.

Lời giải

Cách 1: Ta có

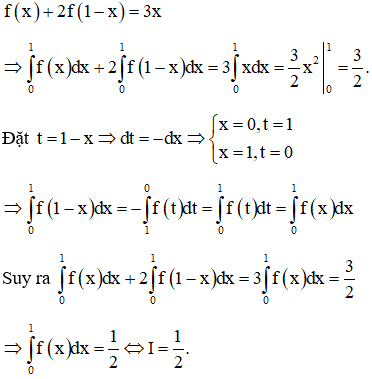
Chọn C.

Cách 2:

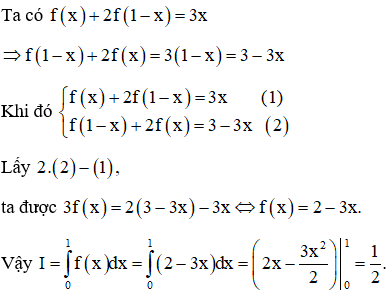
Chọn C.

Dạng 4. Tích phân hàm phân thức hữu tỉ

Phương pháp giải: Thực hiện theo các bước ở lý thuyết.

Chú ý: Cách phân tích hàm phân thức hữu tỉ (giống phần nguyên hàm): Sử dụng phương pháp đồng nhất hệ số để phân tích.

Ví dụ minh họa

Ví dụ 4. Tính tích phân $I=\underset{0}{\overset{3}{\int }}\frac{x^2}{{\left(1+x\right)}^3}dx$?

A. $I=\ln 4+\frac{33}{32}$

B. $I=\ln 4-\frac{4121}{4000}$

C. $I=\ln 4-1$

D. $I=\ln 4-\frac{33}{32}$

Lời giải

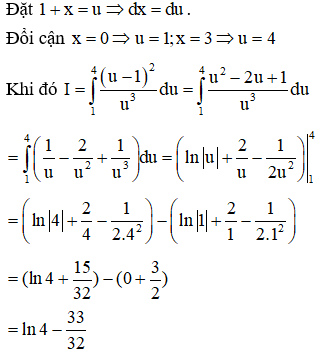
Chọn D.

2. Phương pháp tích phân từng phần

Phương pháp giải: Sử dụng công thức tích phân từng phần

$\underset{a}{\overset{b}{\int }}udv={\left.uv\right|}_a^b-\underset{a}{\overset{b}{\int }}vdu$

Chú ý: Cách chọn u, v (theo bảng đã cho ở phần lý thuyết)

Ví dụ minh họa

Ví dụ 1: Cho tích phân $I=\underset{0}{\overset{\pi }{\int }}{x}^2\cos xdx$ và $u=x^2;dv=\cos xdx$. Khẳng định nào sau đây đúng?

A. $I={\left.x^2\sin x\right|}_0^{\pi }-\underset{0}{\overset{\pi }{\int }}x\sin xdx$

B. $I={\left.x^2\sin x\right|}_0^{\pi }+\underset{0}{\overset{\pi }{\int }}x\sin xdx$

C. $I={\left.x^2\sin x\right|}_0^{\pi }+2\underset{0}{\overset{\pi }{\int }}x\sin xdx$

D. $I={\left.x^2\sin x\right|}_0^{\pi }-2\underset{0}{\overset{\pi }{\int }}x\sin xdx$

Lời giải

Ta có :

$\left\{\begin{array}{l}u=x^2\\ dv=\cos xdx\end{array}\right.\Rightarrow \left\{\begin{array}{l}du=2xdx\\ v=\sin x\end{array}\right.$

Theo công thức tích phân từng phần:

$\Rightarrow I={\left.x^2\sin x\right|}_0^{\pi }-2\underset{0}{\overset{\pi }{\int }}x\sin xdx$

Chọn D.

Ví dụ 2: Cho tích phân $I=\underset{2}{\overset{3}{\int }}\left(3x^2+1\right)\ln xdx=a\ln 3+b\ln 2+c$ với $a,b,c\in \mathbb{Q}$. Khẳng định nào dưới đây là khẳng định đúng?

A. a = 3b.

B. a = – 3b

C. a + b = 40

D. a – b = 20.

Lời giải

Đặt :

$\left\{\begin{array}{l}u=\ln x\\ dv=\left(3x^2+1\right)dx\end{array}\right.\iff \left\{\begin{array}{l}du=\frac{dx}{x}\\ v=x^3+x\end{array}\right.$

Theo công thức tích phân từng phần'

$$\begin{gathered} \Rightarrow I={\left.\left(x^3+x\right)\ln x\right|}_2^3-\underset{2}{\overset{3}{\int }}\left(x^2+1\right)dx \\ =30\ln 3-10\ln 2-{\left.\left(\frac{x^3}{3}+x\right)\right|}_2^3 \\ =30\ln 3-10\ln 2-\frac{22}{3} \\ \Rightarrow a=30;b=-10;c=-3b \end{gathered}$$

Chọn B.

Ví dụ 3. Cho $I=\underset{1}{\overset{2}{\int }}\left(1+x+\frac{1}{x}\right)e^{x-\frac{1}{x}}dx=a{e}^b-c$ với $a;b;c\in ℝ$; $a\ne 0$. Lúc này $S=a+b+c$ có giá trị bằng

A. $S=-\frac{1}{2}$

B. $S=-\frac{3}{2}$

C. $S=\frac{1}{3}$

D. $S=\frac{9}{2}$

Lời giải

Ta có:

Từ (1); (2) ta có

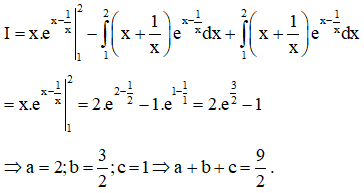
Chọn D.

C. BÀI TẬP TỰ LUYỆN.

Câu 1. Cho hàm số f liên tục trên R và hai số thực a < b. Nếu $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=\alpha$ thì tích phân $\underset{\frac{a}{2}}{\overset{\frac{b}{2}}{\int }}f\left(2x\right)dx$ có giá trị bằng

A. $\frac{\alpha }{2}$

B. $2\alpha$

C. $\alpha$

D. $4\alpha$

Câu 2. Bài toán tính tích phân $I=\underset{1}{\overset{e}{\int }}\frac{\sqrt{\ln x+1}\ln x}{x}dx$ được một học sinh giải theo ba bước sau:

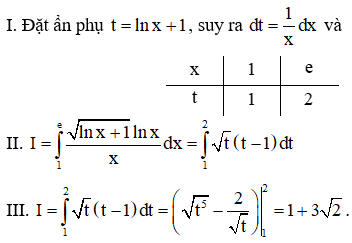
Học sinh này giải đúng hay sai? Nếu sai thì sai từ bước nào?

A. Bài giải đúng.

B. Sai từ Bước II.

C. Sai từ Bước I.

D. Sai ở Bước III.

Câu 3. Bài toán tính tích phân $I=\underset{-2}{\overset{1}{\int }}{(x+1)}^{2}dx$ được một học sinh giải theo ba bước sau:

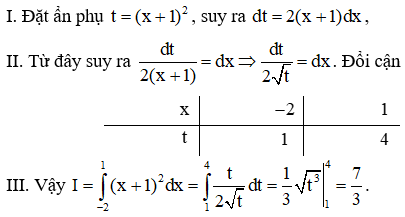
Học sinh này giải đúng hay sai? Nếu sai thì sai từ bước nào?

A. Sai từ Bước I.

B. Sai ở Bước III.

C. Sai từ Bước II.

D. Bài giải đúng.

Câu 4. Cho tích phân: $I=\underset{1}{\overset{e}{\int }}\frac{\sqrt{1-\ln x}}{2x}dx$. Đặt $u=\sqrt{1-\ln x}$ . Khi đó I bằng

A. $I=\underset{1}{\overset{0}{\int }}{u}^{2}du$

B. $I=-\underset{1}{\overset{0}{\int }}{u}^{2}du$

C. $I=\underset{1}{\overset{0}{\int }}\frac{u^2}{2}du$

D. $I=-\underset{0}{\overset{1}{\int }}{u}^{2}du$

Câu 5. Tích phân $\underset{0}{\overset{1}{\int }}\frac{x^7}{{(1+x^2)}^5}dx$ bằng

A. $\frac{1}{2}\underset{1}{\overset{2}{\int }}\frac{{(t-1)}^3}{t^5}dt$

B. $\underset{1}{\overset{3}{\int }}\frac{{(t-1)}^3}{t^5}dt$

C. $\frac{1}{2}\underset{1}{\overset{2}{\int }}\frac{{(t-1)}^3}{t^4}dt$

D. $\frac{3}{2}\underset{1}{\overset{4}{\int }}\frac{{(t-1)}^3}{t^4}dt$.

Câu 6. Tích phân $\underset{1}{\overset{e}{\int }}(2x-5)\ln xdx$ bằng

A. $-{\left.(x^2-5x)\ln x\right|}_1^e-\underset{1}{\overset{e}{\int }}(x-5)dx$

B. ${\left.(x^2-5x)\ln x\right|}_1^e+\underset{1}{\overset{e}{\int }}(x-5)dx$.

C. ${\left.(x^2-5x)\ln x\right|}_1^e-\underset{1}{\overset{e}{\int }}(x-5)dx$

D. ${\left.(x-5)\ln x\right|}_1^e-\underset{1}{\overset{e}{\int }}(x^2-5x)dx$.

Câu 7. Tìm m để $\underset{m}{\overset{2}{\int }}{(3-2x)}^{4}dx=\frac{122}{5}$?

A. 0

B. 9.

C. 7

D. 2.

Câu 8. Tích phân $I=\underset{0}{\overset{1}{\int }}x\sqrt{x^2+1}dx$ có giá trị là

A. $\frac{3\sqrt{2}-1}{3}$

B. $\frac{2\sqrt{2}-1}{3}$

C. $\frac{2\sqrt{2}-1}{2}$

D. $\frac{3\sqrt{2}-1}{2}$.

Câu 9. Giá trị của tích phân $\underset{0}{\overset{1}{\int }}\frac{4x+2}{x^2+x+1}dx$ là

A. ln2.

B. ln3.

C. 2ln2.

D. 2ln3.

Câu 10. Giá trị của tích phân $\underset{0}{\overset{3}{\int }}\frac{x-3}{3.\sqrt{x+1}+x+3}dx$ là

A. $3+3\ln \frac{3}{2}$

B. $3+6\ln \frac{3}{2}$

C. $-3+6\ln \frac{3}{2}$

D. $-3+3\ln \frac{3}{2}$

Câu 11. Giá trị của tích phân $I=\underset{0}{\overset{1}{\int }}\frac{dx}{1+e^x}$ là

A. $\ln \left(\frac{2e}{e+1}\right)$

B. $\ln \left(\frac{e}{e+1}\right)$

C. $2\ln \left(\frac{e}{e+1}\right)$

D. $2\ln \left(\frac{2e}{e+1}\right)$.

Câu 12. Giá trị của tích phân $I=\underset{0}{\overset{\ln 3}{\int }}\frac{e^x}{{\left(e^x+1\right)}^3}dx$ là

A. $2\sqrt{2}-1$

B. $\sqrt{2}-1$

C. $\sqrt{2}-2$

D. $2\sqrt{2}-2$

Câu 13. Giá trị của tích phân $I=\underset{e}{\overset{e^2}{\int }}\frac{dx}{x\ln x}$ là

A. 2ln3.

B. ln3

C. ln2.

D. 2ln2.

Câu 14. Giá trị của tích phân $I=\underset{-8}{\overset{-3}{\int }}\frac{dx}{x\sqrt{1-x}}dx$ là

A. $\ln \frac{2}{3}$

B. 2.

C. –ln2.

D. 2ln2.

Câu 15. Biết $I=\underset{1}{\overset{a}{\int }}\frac{x^3-2\ln x}{x^2}dx=\frac{1}{2}+\ln 2$. Giá trị của a là

A. 2.

B. ln2.

C. $\pi$

D. 3.

Câu 16. Kết quả phép tính tích phân $I=\underset{1}{\overset{5}{\int }}\frac{dx}{x\sqrt{3x+1}}$ có dạng $I=a\ln 3+b\ln 5$ $(a,b\in \mathbb{Z})$. Khi đó $a^2+ab+3b^2$ có giá trị là

A. 1

B. 5

C. 0.

D. 4.

Câu 17. Biết rằng $\underset{0}{\overset{b}{\int }}6dx=6$ và $\underset{0}{\overset{a}{\int }}x{e}^{x}dx=a$. Khi đó biểu thức $b^2+a^3+3a^2+2a$ có giá trị bằng

A. 5

B. 4

C. 7

D. 3.

Câu 18. Giả sử $\underset{1}{\overset{2}{\int }}\left(2x-1\right)\ln x\text{d}x=a\ln 2+b$, $\left(a;b\in \mathbb{Q}\right)$. Tính a + b.

A. $\frac{5}{2}$

B. 2

C. 2.

D. $\frac{3}{2}$.

Câu 19. Biết rằng $\underset{0}{\overset{\ln 2}{\int }}\frac{1}{2e^x+1}\text{dx=}{\ln }^{a}2+b\ln 3+\ln 5^c$. Trong đó a, b, c là các số nguyên. Khi đó S = a + b – c bằng bao nhiêu.

A. S = 4

B. S = 3.

C. S = 5

D. S = 2.

Câu 20. Cho hàm số y = f(x) là hàm lẻ và liên tục trên [-4;4], biết $\underset{-2}{\overset{0}{\int }}f(-x)dx=2$ và $\underset{1}{\overset{2}{\int }}f(-2x)dx=4$. Tính $I=\underset{0}{\overset{4}{\int }}f\left(x\right)dx=?$

A. -10.

B. -6.

C. 6.

D. 10.

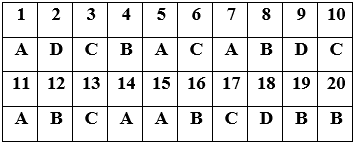
Đáp án