100 bài tập về nguyên hàm của hàm số lượng giác (2024 có đáp án) và cách giải các dạng toán

Nguyên hàm của hàm số lượng giác và cách giải 

A. LÝ THUYẾT.

1. Một số công thức lượng giác cần nhớ

- Hệ thức lượng giác cơ bản:

$$\begin{gathered} {\sin }^{2}x+{\cos }^{2}x=1; \\ \frac{1}{{\sin }^{2}x}=1+{\cot }^{2}x; \\ \frac{1}{{\cos }^{2}x}=1+{\tan }^{2}x \end{gathered}$$

2. Một số nguyên hàm lượng giác cơ bản

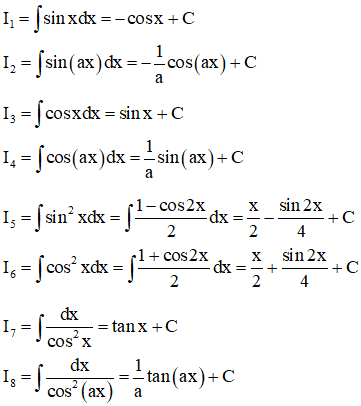
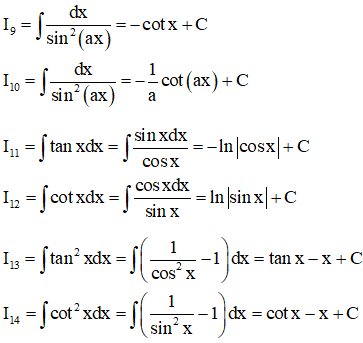
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI

a) Dạng 1 :  $\int {\sin }^{m}x.{\cos }^{n}xdx$ trong đó m, n là các số tự nhiên.

Trường hợp 1: Trong hai số m, n có ít nhất một số lẻ.

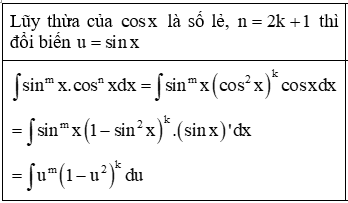
Trường hợp 2: Cả hai số m, n đều là số chẵn: Ta sử dụng công thức hạ bậc để giảm một nửa số mũ của , để làm bài toán trở nên đơn giản hơn.

b) Dạng 2 :  $\int \sin ax.\cos bxdx$;$\int \sin ax.\sin bxdx$; $\int \cos ax.\cos bxdx$;$\int \cos ax.\sin bxdx$.

Ta sử dụng công thức biến đổi tích thành tổng trong lượng giác.

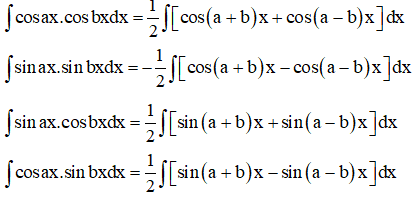
c) Dạng 3 :  $\int \frac{{\tan }^{m}x}{{\cos }^{n}x}dx$ trong đó m, n là các số nguyên.

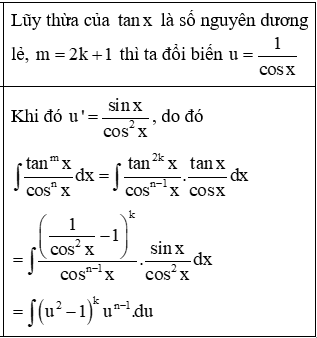
d) Dạng 4 : Đổi biến số với hàm lượng giác.

Khi nguyên hàm, tích phân của các hàm số mà biểu thức của nó có chứa các dạng $\sqrt{x^2+a^2},\sqrt{x^2-a^2},\sqrt{a^2-x^2}$, thì ta có cách biến đổi lượng giác như sau:

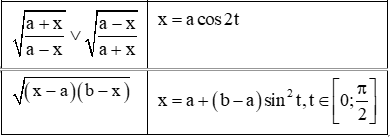
C. VÍ DỤ MINH HOẠ

Ví dụ 1: Tìm $I=\int {\sin }^{5}x.{\cos }^{2}xdx$.

Lời giải

Vì lũy thừa của $\sin x$ là số lẻ nên ta đổi biến

$u=\cos x\Rightarrow du=\left(\cos x\right)\text{'}dx$

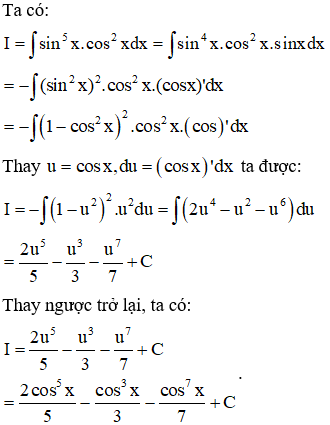
Ví dụ 2: Tìm nguyên hàm

a. $A=\int \frac{{\tan }^{6}x}{{\cos }^{4}x}dx$

b. $B=\int \frac{{\tan }^{5}x}{{\cos }^{7}x}dx$

Lời giải

a. Do lũy thừa của cosx là số nguyên dương chẵn nên đặt u = tanx. Từ công thức tổng quát đã chứng minh ở trên ta có:

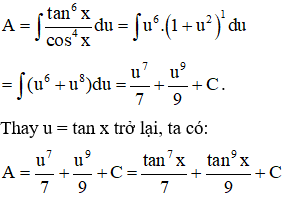
b. Do lũy thừa của là một số lẻ nên ta đặt $u=\frac{1}{\cos x}$, do vậy, từ công thức tổng quát chứng minh ở trên ta có

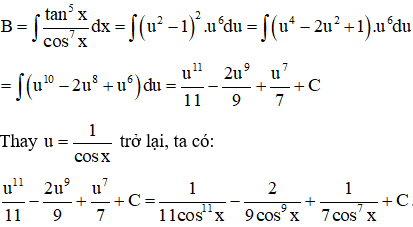
Ví dụ 3: Cho hàm số f(x) thỏa mãn $f\text{'}\left(x\right)=x+\sin x\sin 2x.$ Biết rằng f(0) = 2. Giá trị của $f\left(\frac{\pi }{2}\right)$ là:

A. $f\left(\frac{\pi }{2}\right)=\frac{{\pi }^2}{4}+\frac{2}{3}$

B. $f\left(\frac{\pi }{2}\right)=\frac{{\pi }^2}{4}+\frac{8}{3}$

C. $f\left(\frac{\pi }{2}\right)=\frac{{\pi }^2}{2}+\frac{2}{3}$

D. $f\left(\frac{\pi }{2}\right)=\frac{{\pi }^2}{2}+\frac{8}{3}$

Lời giải:

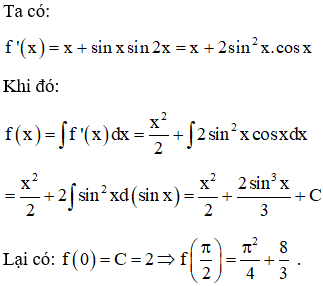
Chọn B

D. BÀI TẬP TỰ LUYỆN.

Câu 1. Tìm công thức sai:

A. $\int e^{x}dx=e^x+C$

B. $\int a^{x}dx=\frac{a^x}{\ln a}+C\left(0<a\ne 1\right)$

C. $\int \cos xdx=\sin x+C$

D. $\int \sin xdx=\cos x+C$

Câu 2. Tìm nguyên hàm của: $y=\sin x.\sin 7x$ với $F\left(\frac{\pi }{2}\right)=0$ là:

A. $\frac{\sin 6x}{12}+\frac{\sin 8x}{16}$

B. $-\frac{\sin 6x}{12}+\frac{\sin 8x}{16}$

C. $\frac{\sin 6x}{12}-\frac{\sin 8x}{16}$

D. $-\left[\frac{\sin 6x}{12}+\frac{\sin 8x}{16}\right]$

Câu 3. $\int \frac{1}{{\sin }^{2}x.{\cos }^{2}x}dx$ bằng:

A. $2\tan 2x+C$

B. -4$\cot 2x+C$

C. 4$\cot 2x+C$

D. 2$\cot 2x+C$

Câu 4. $\int {\left(\sin 2x-c\text{os}2x\right)}^{2}dx$ bằng:

A. $\frac{{\left(\sin 2x-c\text{os}2x\right)}^3}{3}+C$

B. ${\left(-\frac{1}{2}c\text{os}2x+\frac{1}{2}\sin 2x\right)}^2+C$

C. $x-\frac{1}{2}\sin 2x+C$

D. $x+\frac{1}{4}c\text{os}4x+C$

Câu 5. $\int c{\text{os}}^2\frac{2x}{3}dx$ bằng:

A. $\frac{3}{2}c{\text{os}}^4\frac{2x}{3}+C$

B. $\frac{1}{2}c{\text{os}}^4\frac{2x}{3}+C$

C. $\frac{x}{2}+\frac{3}{8}\text{sin}\frac{4x}{3}+C$

D. $\frac{x}{2}-\frac{4}{3}c\text{os}\frac{4x}{3}+C$

Câu 6. Hàm số $F\left(x\right)=\ln \left|\sin x-3\cos x\right|$ là một nguyên hàm của hàm số nào trong các hàm số sau đây:

A. $f\left(x\right)=\frac{\cos x+3\sin x}{\sin x-3\cos x}$

B. $f\left(x\right)=\cos x+3\sin x$

C. $f\left(x\right)=\frac{-\cos x-3\sin x}{\sin x-3\cos x}$

D. $f\left(x\right)=\frac{\sin x-3\cos x}{\cos x+3\sin x}$

Câu 7. Tìm nguyên hàm: $\int {(1+\sin x)}^{2}dx$

A. $\frac{2}{3}x+2\cos x-\frac{1}{4}\sin 2x+C$

B. $\frac{3}{2}x-2\cos x+\frac{1}{4}\sin 2x+C$

C. $\frac{2}{3}x-2\cos 2x-\frac{1}{4}\sin 2x+C$

D. $\frac{3}{2}x-2\cos x-\frac{1}{4}\sin 2x+C$

Câu 8. Cho $f\left(x\right)=\frac{4m}{\pi }+{\sin }^{2}x$. Tìm m để nguyên hàm F(x) của f(x) thỏa mãn F(0) = 1 và $F\left(\frac{\pi }{4}\right)=\frac{\pi }{8}$

A. $m=-\frac{4}{3}$

B. $m=-\frac{3}{4}$

C. $m=-\frac{3}{4}$

D. $m=\frac{3}{4}$

Câu 9. Một nguyên hàm của hàm số $y=\sin 3x$

A. $-\frac{1}{3}c\text{os}3x$

B. $-3c\text{os}3x$

C. $3c\text{os}3x$

D. $\frac{1}{3}c\text{os}3x$

Câu 10. Nguyên hàm của hàm số $f\left(x\right)=ta{n}^{3}x$ là:

A. Đáp án khác

B. ${\tan }^{2}x+1$

C. $\frac{{\tan }^{4}x}{4}+C$

D. $\frac{1}{2}{\tan }^{2}x+\ln \left|\cos x\right|+C$

Câu 11. Cặp hàm số nào sau đây có tính chất: Có một hàm số là nguyên hàm của hàm số còn lại?

A. $\sin 2x$ và ${\cos }^{2}x$

B. $\tan x^2$ và $\frac{1}{{\cos }^2{x}^2}$

C. $e^x$ và $e^{-x}$

D. $\sin 2x$ và ${\sin }^{2}x$

Câu 12. Một nguyên hàm của hàm số $f\left(x\right)=\frac{4}{{\cos }^{2}x}$ là:

A. $\frac{4x}{{\sin }^{2}x}$

B. $4\tan x$

C. $4+\tan x$

D. $4x+\frac{4}{3}{\tan }^{3}x$

Câu 13. Họ nguyên hàm của $f\left(x\right) = {\sin }^{3}x$

A. $\cos x-\frac{{\cos }^{3}x}{3}+C$

B. $-\cos x+\frac{{\cos }^{3}x}{3}+C$

C. $-\cos x+\frac{1}{\cos x}+c$

D. $\frac{{\sin }^{4}x}{4}+C$

Câu 14. Nguyên hàm của hàm số $f\left(x\right)=2\sin x+\cos x$ là:

A. $2\cos x-\mathrm{s}\text{inx}+C$

B. $2\cos x+\mathrm{s}\text{inx}+C$

C. $-2\cos x-\mathrm{s}\text{inx}+C$

D. $-2\cos x+\mathrm{s}\text{inx}+C$

Câu 15. Họ nguyên hàm của hàm số $f\left(x\right)=\sin 2x$ là

A. $F\left(x\right)=-\frac{1}{2}\cos 2x+C$

B. $F\left(x\right)=\cos 2x+C$

C. $F\left(x\right)=\frac{1}{2}\cos 2x+C$

D. $F\left(x\right)=-\cos 2x+C$

Câu 16. Tính $\int \cos 5x.\cos 3xdx$

A. $\frac{1}{8}\sin 8x+\frac{1}{2}\sin 2x+C$

B. $\frac{1}{2}\sin 8x+\frac{1}{2}\sin 2x$

C. $\frac{1}{16}\sin 8x+\frac{1}{4}\sin 2x$

D. $\frac{-1}{16}\sin 8x-\frac{1}{4}\sin 2x$

Câu 17. $\int c\text{os}8x.\sin xdx$ bằng:

A. $\frac{1}{8}\sin 8x.c\text{os}x+C$

B. $-\frac{1}{8}\sin 8x.c\text{os}x+C$

C. $\frac{1}{14}c\text{os7}x-\frac{1}{18}c\text{os}9x+C$

D. $\frac{1}{18}c\text{os9}x-\frac{1}{14}c\text{os7}x+C$

Câu 18. $\int {\sin }^{2}2xdx$ bằng:

A. $\frac{1}{2}x+\frac{1}{8}\sin 4x+C$

B. $\frac{1}{3}{\sin }^{3}2x+C$

C. $\frac{1}{2}x-\frac{1}{8}\sin 4x+C$

D. $\frac{1}{2}x-\frac{1}{4}\sin 4x+C$

Câu 19. Nguyên hàm F(x) của hàm số $f\left(x\right)=x+\sin x$ thỏa mãn $F\left(0\right)=19$ là:

A. $F\left(x\right)=-c\text{os}x+\frac{x^2}{2}$

B. $F\left(x\right)=-c\text{os}x+\frac{x^2}{2}+2$

C. $F\left(x\right)=c\text{os}x+\frac{x^2}{2}+20$

D. $F\left(x\right)=-c\text{os}x+\frac{x^2}{2}+20$

Câu 20. Nguyên hàm F(x) của hàm số $f\left(x\right)=2x+\frac{1}{{\sin }^{2}x}$ thỏa mãn $F\left(\frac{\pi }{4}\right)=-1$ là:

A. $F\left(x\right)=-c\text{ot}x+x^2-\frac{{\pi }^2}{4}$

B. $F\left(x\right)=c\text{ot}x-x^2+\frac{{\pi }^2}{16}$

C. $F\left(x\right)=-c\text{ot}x+x^2$

D. $F\left(x\right)=-c\text{ot}x+x^2-\frac{{\pi }^2}{16}$

Câu 21. Cho hàm số $f\left(x\right)=\cos 3x.\cos x$. Nguyên hàm của hàm số $f\left(x\right)$ bằng 0 khi $x=0$ là hàm số nào trong các hàm số sau ?

A. $3\sin 3x+\sin x$

B. $\frac{\sin 4x}{8}+\frac{\sin 2x}{4}$

C. $\frac{\sin 4x}{2}+\frac{\sin 2x}{4}$

D. $\frac{\cos 4x}{8}+\frac{\cos 2x}{4}$

Câu 22. $\int \frac{3\cos x}{2+\sin x}dx$ bằng:

A. $3\ln \left(2+\sin x\right)+C$

B. $-3\ln \left|2+\sin x\right|+C$

C. $\frac{3\sin x}{{\left(2+\sin x\right)}^2}+C$

D. $-\frac{3\sin x}{\ln \left(2+\sin x\right)}+C$

Câu 23. Nguyên hàm của $\frac{\sin x+\cos x}{\sin x-\cos x}$ là:

A. $\ln \left|\sin x+\cos x\right|+C$

B. $\frac{1}{\ln \left|\sin x-\cos x\right|}+C$

C. $\ln \left|\sin x-\cos x\right|+C$

D. $\frac{1}{\sin x+\cos x}+C$

Câu 24. $\int \frac{\cot x}{{\sin }^{2}x}dx$ bằng:

A. $-\frac{{\cot }^{2}x}{2}+C$

B. $\frac{{\cot }^{2}x}{2}+C$

C. $-\frac{{\tan }^{2}x}{2}+C$

D. $\frac{{\tan }^{2}x}{2}+C$

Câu 25. $\int \frac{\sin x}{c{\text{os}}^{5}x}dx$ bằng:

A. $\frac{-1}{4c{\text{os}}^{4}x}+C$

B. $\frac{1}{4c{\text{os}}^{4}x}+C$

C. $\frac{1}{4{\text{sin}}^{4}x}+C$

D. $\frac{-1}{4{\text{sin}}^{4}x}+C$

Câu 26. $\int {\sin }^{5}x.c\text{os}xdx$ bằng:

A. $\frac{{\sin }^{6}x}{6}+C$

B.$-\frac{{\sin }^{6}x}{6}+C$

C. $-\frac{c{\text{os}}^{6}x}{6}+C$

D. $\frac{c{\text{os}}^{6}x}{6}+C$

Câu 27. Họ nguyên hàm của hàm số $f\left(x\right)=e^{-x}\cos x$ là

A. $F\left(x\right)=\frac{1}{2}{e}^{-x}\left(\sin x-\cos x\right)+C$

B. $F\left(x\right)=\frac{1}{2}{e}^{-x}\left(\sin x+\cos x\right)+C$

C. $F\left(x\right)=-\frac{1}{2}{e}^{-x}\left(\sin x+\cos x\right)+C$

D. $F\left(x\right)=-\frac{1}{2}{e}^{-x}\left(\sin x-\cos x\right)+C$

Câu 28. Nguyên hàm của hàm số: $I=\int \left(x-2\right)\sin 3xdx$ là:

A. F(x) = $-\frac{\left(x-2\right)\cos 3x}{3}+\frac{1}{9}\sin 3x+C$

B. F(x) = $\frac{\left(x-2\right)\cos 3x}{3}+\frac{1}{9}\sin 3x+C$

C. F(x) = $-\frac{\left(x+2\right)\cos 3x}{3}+\frac{1}{9}\sin 3x+C$

D. F(x) = $-\frac{\left(x-2\right)\cos 3x}{3}+\frac{1}{3}\sin 3x+C$

Câu 29. Biểu thức nào sau đây bằng với $\int x^2\sin xdx$?

A. $-2x\cos x-\int x^2\cos xdx$

B. $-x^2\cos x+\int 2x\cos xdx$

C. $-x^2\cos x-\int 2x\cos xdx$

D. $-2x\cos x+\int x^2\cos xdx$

Câu 30. Đổi biến x = 2sint tích phân $I=\underset{}{\overset{}{\int }}\frac{dx}{\sqrt{4-x^2}}$ trở thành

A. $\underset{}{\overset{}{\int }}dt$

B. $\underset{}{\overset{}{\int t}}dt$

C. $\underset{}{\overset{}{\int }}\frac{1}{t}dt$

D. $\underset{}{\overset{}{\int }}dt$

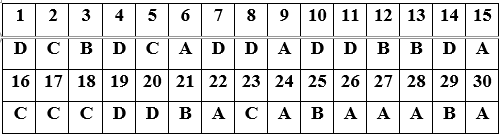
Đáp án