100 công thức về nguyên hàm cơ bản, đẩy đủ, chi tiết nhất (2024) và cách giải các dạng toán
Công thức và cách giải các dạng toán về nguyên hàm gồm phương pháp giải, ví dụ minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập các dạng toán về nguyên hàm. Mời các bạn đón xem:
Các công thức nguyên hàm cơ bản đầy đủ, chi tiết nhất
1. Lý thuyết
a) Định nghĩa:
Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi .
Định lí:
1) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.
Do đó là họ tất cả các nguyên hàm của f(x) trên K. Ký hiệu .
b) Tính chất của nguyên hàm
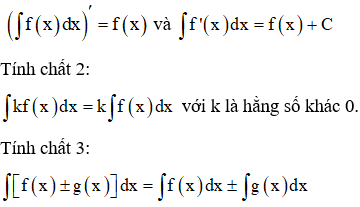
c) Sự tồn tại của nguyên hàm
Định lí: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.
d) Bảng nguyên hàm của một số hàm số sơ cấp
Nhận xét. Khi thay x bằng (ax + b) thì lấy nguyên hàm nhân kết quả thêm
2. Ví dụ minh họa
Ví dụ 1: Tính nguyên hàm của các hàm số sau:
a) f(x)= x3 + 3x + 2
b)
c) f(x) = (x + 1)(x + 2)
d)
Lời giải
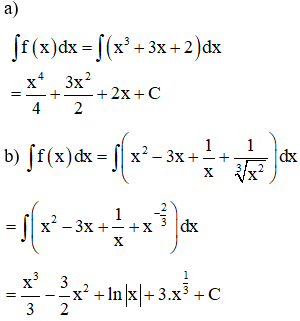
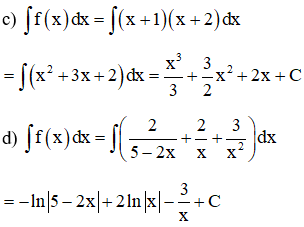
Ví dụ 2: Tính các nguyên hàm
a)
b)
c)
Lời giải
a)
b)
c)