100 công thức về phép đối xứng trục (2024 có đáp án) và cách giải các dạng toán

Công thức phép đối xứng trục 

1. Lý thuyết

Cho đường thẳng d. Phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành M’ sao cho d là đường trung trực của đoạn thẳng MM’ được gọi là phép đối xứng qua đường thẳng d hay phép đối xứng trục d.

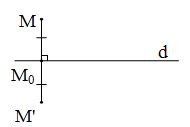
Phép đối xứng trục d thường được kí hiệu là Đ_d.

* Tính chất

- Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm.

- Biến đường thẳng thành đường thẳng .

- Biến đoạn thẳng thành đoạn thẳng bằng nó.

- Biến tam giác thành tam giác bằng nó.

- Biến đường tròn thành đường tròn có cùng bán kính.

2. Công thức

Cho đường thẳng d, điểm M’(x’;y’) đối xứng với M(x;y) qua d. Gọi M₀(x₀;y₀) là hình chiếu vuông góc của M trên đường thẳng d. Khi đó M'= Đ_d(M)$\iff \overrightarrow{M_{0}M\text{'}}=-\overrightarrow{M_{0}M}.$$\Rightarrow \left\{\begin{array}{l}x\text{'}=2x_0-x\\ y\text{'}=2y_0-y\end{array}\right.$

- Nếu $d\equiv Ox$. Gọi M’(x’;y’) = Đ_Ox[M(x; y)] thì $\left\{\begin{array}{l}x\text{'}=x\\ y\text{'}=-y\end{array}\right..$

- Nếu $d\equiv Oy.$ Gọi M’(x’;y’) = Đ_Oy[M(x; y)] thì $\left\{\begin{array}{l}x\text{'}=-x\\ y\text{'}=y\end{array}\right..$

- Nếu d: Ax + By + C = 0 với $A^2+B^2\ne 0$. Gọi M’(x’;y’) = Đ_Oy[M(x; y)] thì

$\left\{\begin{array}{l}x\text{'}=x-\frac{2A\left(Ax+By+C\right)}{A^2+B^2}\\ y\text{'}=-y-\frac{2B\left(Ax+By+C\right)}{A^2+B^2}\end{array}\right..$

3. Ví dụ minh họa

Ví dụ 1: Cho điểm M(2;4).

a) Tìm tọa đô M’ là ảnh của M qua phép đối xứng trục Oy.

b) Tìm tọa độ của M’’ là ảnh của M’ qua phép đối xứng trục Ox.

Lời giải

a) Đ_Oy(M)=M’ $\Rightarrow \left\{\begin{array}{l}x\text{'}=-x=-2\\ y\text{'}=y=4\end{array}\right.\Rightarrow M\text{'}(-2;4)$

b) Đ_Ox(M’)=M’’$\Rightarrow \left\{\begin{array}{l}x"=x\text{'}=-2\\ y"=-y\text{'}=-4\end{array}\right.\Rightarrow M"(-2;-4)$

Ví dụ 2: Cho đường tròn (C): (x − 2)² + (y − 3)² = 9. Viết phương trình đường tròn (C’) là ảnh của đường tròn (C) qua phép đối xứng trục Ox.

Lời giải

Ta có: Đường tròn (C) có tâm I(2;3) và bán kính R = 3.

Đường tròn (C’) là ảnh của đường tròn (C) qua phép đối xứng trục Ox.

Khi đó (C’) có bán kính R = 3 và tâm I’ là ảnh của I qua phép đối xứng trục Ox.

Ta có: I’ = Đ_Ox(I)$\Rightarrow \left\{\begin{array}{l}{x}_{I\text{'}}=x_I=2\\ y_{I\text{'}}=-y_I=-3\end{array}\right.\Rightarrow I\text{'}(2;-3)$

Vậy phương trình đường tròn (C’) là: (x − 2)² + (y + 3)² = 9.

4. Bài tập tự luyện

Câu 1. Trong mặt phẳng tọa độ Oxy, cho điểm M(2;3). Hỏi trong bốn điểm sau điểm nào là ảnh của M qua phép đối xứng trục Ox?

A.  M’₁(3; 2)

B.  M’₂(2; -3)

C.  M’₃(3; -2)

D.  M’₄(-2; 3)

Câu 2. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với A(1; 5), B(-1; 2), C(6; -4). Gọi G là trọng tâm của tam giác ABC. Phép đối xứng trục Đ_Oy biến điểm G thành điểm G’ có tọa độ là:

A. G’(-2; -1)

B. G’ (2; -4)

C. G’ (0; -3)

D. G’ (-2; 1)

Câu 3. Trong mặt phẳng tọa độ Oxy cho đường thẳng d: x + y – 2 = 0. Ảnh của đường thẳng d qua phép đối xứng trục Ox có phương trình là:

A. x – y – 2 = 0

B. x + y + 2 = 0

C. x + y – 2 = 0

D. x – y + 2 = 0

Đáp án: 1B, 2D, 3A