100 công thức lũy thừa cần nhớ (2024) và cách giải các dạng bài tập

Công thức lũy thừa đầy đủ, chi tiết nhất 

I. Lý thuyết về lũy thừa

1. Định nghĩa

Lũy thừa là một phép toán hai ngôi của toán học thực hiện trên hai số a và b, kết quả của phép toán lũy thừa là tích của phép nhân có n thừa số a nhân với nhau

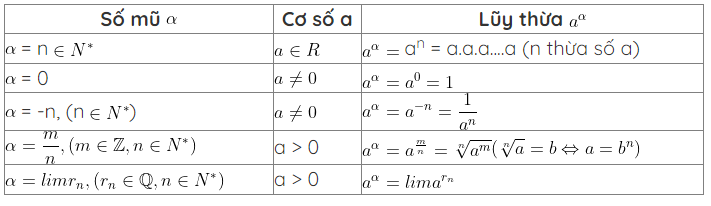
2. Các loại lũy thừa

Dạng 1. Căn bậc n

- Cho số thực b và số nguyên dương $n\ge 2$.Số a được gọi là căn bậc n của số b nếu $a^n=b$

VD: 4 là căn bậc ba của 64 vì $4^3=64$

- Khi n lẻ, $b\in ℝ$: Tồn tại duy nhất $\sqrt[n]{b}$

Dạng 2. Lũy thừa với số mũ nguyên

- Lũy thừa với số mũ nguyên dương

Cho $a\in ℝ$, $n\in {\mathbb{N}}^{*}$. Khi đó: $a^n=\underset{nsôa}{\underbrace{a.a\mathrm{...}a}}$

- Lũy thừa với số mũ nguyên âm, lũy thừa với số mũ 0

Cho $a\ne 0$. Khi đó: $a^{-n}=\frac{1}{a^n};a^0=1$

VD: $2^{-3}=\frac{1}{2^3}=\frac{1}{8}$

Chú ý: Lũy thừa với số mũ nguyên có các tính chất tương tự tính chất của lũy thừa với số mũ nguyên dương.

+ $0^0$ và $0^{-n}$ không có nghĩa.

Dạng 3. Lũy thừa với số mũ hữu tỉ

- Cho số thực $a>0$ và số hữu tỉ $r=\frac{m}{n}$, trong đó $m\in \mathbb{Z},n\ge 2$

Khi đó: $a^r=a^{\frac{m}{n}}=\sqrt[n]{a^m}$. VD: $2^{\frac{1}{3}}=\sqrt[3]{2}$

Dạng 4. Lũy thừa với số mũ vô tỉ

- Giả sử a là một số dương, $\alpha$ là một số vô tỉ, $\left(r_n\right)$ là một dãy số hữu tỉ sao cho $\underset{n\to +\infty }{\lim }{r}_n=\alpha$. Khi đó: $a^{\alpha }=\underset{n\to +\infty }{\lim }{a}^{r_n}$

II. Các tính chất của lũy thừa

Cho 2 số dương a, b; $m,n\in ℝ$. Khi đó:

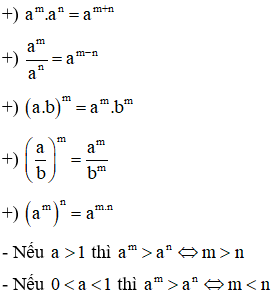
III. Bộ công thức lũy thừa cơ bản

Ngoài ra, còn có những trường hợp đặc biệt như:

- Lũy thừa của số e

- Hàm lũy thừa với số mũ thực

IV. Ví dụ

VD1. Cho a, b là các số dương. Hãy viết rút gọn các biểu thức sau dưới dạng lũy thừa:

a. $a^{\frac{1}{3}}.\sqrt{a}$

b. $b^{\frac{1}{2}}.b^{\frac{1}{3}}.\sqrt[6]{b}$

c. $\sqrt[3]{b}:b^{\frac{1}{6}}$

Lời giải:

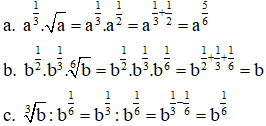
VD2. Tìm x biết:

a. $x^8-15x^4-16=0$

b. $x^6+6x^3-16=0$

Lời giải:

VD3. Cho a và b là các số dương. Rút gọn các biểu thức

a. $A=\frac{a^{\frac{4}{3}}\left(a^{-\frac{1}{3}}+a^{\frac{2}{3}}\right)}{a^{\frac{1}{4}}\left(a^{\frac{3}{4}}+a^{-\frac{1}{4}}\right)}$

b. $B=\left(\sqrt[3]{a}+\sqrt[3]{b}\right).\left(a^{\frac{2}{3}}+b^{\frac{2}{3}}-\sqrt[3]{ab}\right)$

Lời giải:

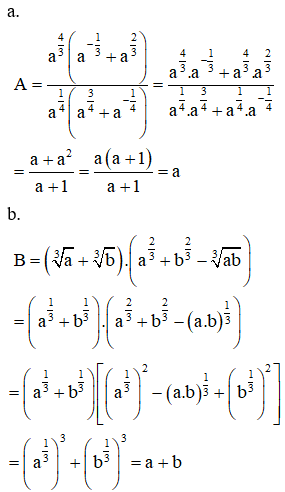
V. Luyện tập

Bài 1. Tính

a. $2^{2-3\sqrt{5}}{.8}^{\sqrt{5}}$

b. $3^{1+2\sqrt[3]{2}}:9^{\sqrt[3]{2}}$

c. $\left(4^{2\sqrt{3}}-4^{\sqrt{3}-1}\right){.2}^{-2\sqrt{3}}$

Bài 2. Cho x và y là 2 số dương. Rút gọn các biểu thức sau:

a. $\frac{x^{\frac{1}{3}}\sqrt{y}+y^{\frac{1}{3}}\sqrt{x}}{\sqrt[6]{x}+\sqrt[6]{y}}$

b. $\left(x^{\frac{1}{3}}+y^{\frac{1}{3}}\right):\left(2+\sqrt[3]{\frac{x}{y}}+\sqrt[3]{\frac{y}{x}}\right)$

Bài 3. Rút gọn và tính giá trị của biểu thức

a. $A=\sqrt[3]{a}.\sqrt[6]{a}$ với $a=0,09$

b. $\frac{\sqrt{b}.\sqrt[3]{b^2}}{\sqrt[6]{b}}$ với $b=1,3$

c. $C=\frac{\sqrt[3]{a}.\sqrt[4]{a}.\sqrt[12]{a^5}}{a^{-\frac{1}{3}}}$ với $a=2,7$

Bài 4. So sánh các cặp số sau:

a. $\sqrt{17}$ và $\sqrt[3]{28}$

b. $\sqrt[4]{13}$ và $\sqrt[5]{23}$

c. ${\left(\frac{2}{3}\right)}^{\sqrt{3}}$ và ${\left(\frac{2}{3}\right)}^{\sqrt{2}}$

d. $3^{\sqrt{5}}$ và $3^{\sqrt{3}+1}$

Bài 5. So sánh các số sau với 1

a. $3^{-2}$

b. ${\left(\frac{1}{2}\right)}^{\sqrt{5}}$

c. ${\left(\frac{\pi }{3}\right)}^{\sqrt{5}-2}$

Bài 6. Giải phương trình

a. $x^{10}-x^5-2=0$

b. $x^9-7x^3+6=0$