100 công thức diện tích hình phẳng, đẩy đủ, chi tiết nhất (2024) và cách giải các dạng toán
Công thức và cách giải các dạng toán về diện tích hình phẳng phần gồm phương pháp giải, ví dụ minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập các dạng toán về diện tích hình phẳng. Mời các bạn đón xem:
Công thức tính diện tích hình phẳng đầy đủ, chi tiết nhất
1. Lý thuyết
Diện tích hình giới hạn bởi hàm số y = f(x) (trong đó y = f(x) liên tục trên [a; b]), trục Ox và hai đường thẳng x = a, x = b được tính theo công thức:
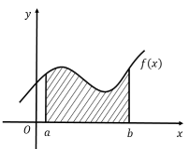
Diện tích hình giới hạn bởi 2 hàm số y = f(x), y = g(x) (trong đó f(x); g(x) liên tục trên đoạn [a; b]) và hai đường thẳng x = a, x = b được tính theo công thức:
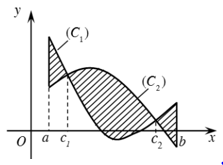
Chú ý: Cách phá dấu giá trị tuyệt đối trong tích phân
- Khi tính tích phân chứa trị tuyện đối nếu f(x) = 0 có một nghiệm thì ta có:
- Khi tính tích phân chứa trị tuyện đối nếu f(x) = 0 có 2 nghiệm và c
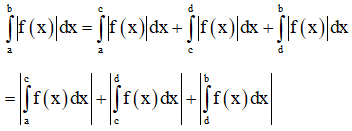
2. Ví dụ minh họa
Ví dụ 1: Tính diện tích hình phẳng giới hạn bởi hai đường cong: y = x3 - 2x2 và y = x2 - 4.
Lời giải
Phương trình hoành độ giao điểm của hai đường cong y = x3 - 2x2 và y = x2 - 4 là:
Ví dụ 2: Tính diện tích hình phẳng giới hạn bởi các đường sau đây: y = x2 + x - 1 và y = x4 + x – 1.
Lời giải
Phương trình hoành độ giao điểm của hai đường cong:
