100 bài tập về hàm số y = |x| (2024 có đáp án) và cách giải các dạng toán

Phương pháp giải Hàm số y = |x| chi tiết, hay nhất

I. Lí thuyết tổng hợp

- Tập xác định của hàm số: y = |x| là D=R𝐷=ℝ.

- Hàm số y = |x|:

+ TH1: y = x nếu x ≥≥ 0

+ TH2: y = -x nếu x < 0

- Tính chẵn, lẻ: Hàm số y = |x| là hàm số chẵn.

- Hàm số ∀x∈R⇒y≥0∀𝑥∈ℝ⇒𝑦≥0. Có đồ thị:

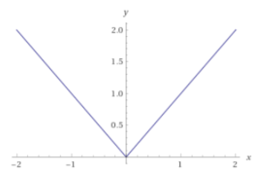
- Tính đồng biến, nghịch biến:

+ Hàm số nghịch biến trên nửa khoảng (−∞;0](−∞;0]

+ Hàm số đồng biến trên nửa khoảng [0;+∞)[0;+∞)

II. Các công thức

- Hàm số y = |x|⇔{y=x(x≥0)y=−x(x<0)⇔𝑦=𝑥(𝑥≥0)𝑦=−𝑥(𝑥<0)

- ∀x∈R⇒y≥0∀𝑥∈ℝ⇒𝑦≥0

- Cách vẽ đồ thị y = |x|.

+ Vẽ hệ trục tọa độ Oxy

+ Chọn điểm A(x0𝑥0;|x0𝑥0|). Lấy điểm đối xứng với nó qua trục tung : A’(-x0𝑥0;|x0𝑥0|).

+ Vẽ tia OA và OA’ tạo nên đồ thị hàm số y = |x|.

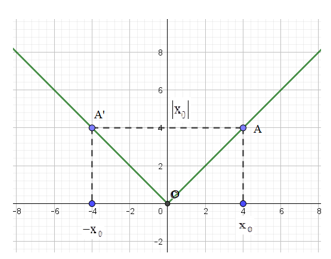
- Nửa khoảng nghịch biến: (−∞;0](−∞;0]

- Nửa khoảng đồng biến: [0;+∞)[0;+∞)

III. Ví dụ minh họa

Bài 1: Chứng minh hàm số y = f(x) = |x| là hàm số chẵn.

Lời giải:

Hàm số y = f(x) = |x| có tập xác định là D=R𝐷=ℝ.

Có ∀x∈D⇒−x∈D∀𝑥∈𝐷⇒−𝑥∈𝐷

Xét:

f(x) = |x|

f(-x) = |-x| = |x|

⇒⇒f(x) = f(-x)

⇒⇒ Hàm số y = f(x) = |x| là hàm số chẵn.

Bài 2: Cho hàm số y = |x|. Tìm các giá trị x để hàm số y có giá trị bằng 5.

Lời giải:

Ta có: y = |x| = 5

Với x ≥≥ 0 ⇒⇒ y = x ⇒⇒ ( thỏa mãn điều kiện x ≥≥ 0 )

Với x < 0 ⇒⇒ y = -x ⇒−x=5⇔x=−5⇒−𝑥=5⇔𝑥=−5 ( thỏa mãn điều kiện x < 0 )

Vậy với x = 5 hoặc x = -5 thì hàm số y có giá trị bằng 5.

Bài 3: Xét tính đồng biến, nghịch biến của hàm số y = |x| trên khoảng (2; 4) và nửa khoảng (-5; -1] sau đó vẽ đồ thị hàm số y = |x|.

Lời giải:

- Hàm số y = |x| đồng biến trên nửa khoảng [0;+∞)[0;+∞). Mà (2; 4)⊂[0;+∞)⊂[0;+∞)

⇒⇒ Hàm số y = |x| đồng biến trên khoảng (2; 4)

- Hàm số y = |x| nghịch biến trên nửa khoảng (-∞;0](-∞;0]. Mà (-5; -1]⊂(-∞;0]⊂(-∞;0]

⇒⇒ Hàm số y = |x| nghịch biến trên nửa khoảng (-5; -1]

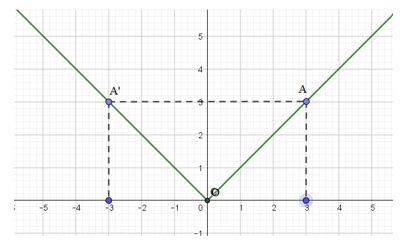
- Vẽ đồ thị hàm số y = |x|.

+ Vẽ hệ trục tọa độ Oxy

+ Chọn điểm A(3; 3) và điểm đối xứng của nó qua trục tung là A’(-3; 3)

+ Vẽ tia OA và OA’ ta có đồ thị:

IV. Bài tập tự luyện

Bài 1: Cho hàm số y = |x| và đường thẳng d: y = 2m. Tìm điều kiện của m để phương trình |x| = 2m vô nghiệm.

Bài 2: Xét tính đồng biến, nghịch biến của hàm số y = |x| trên khoảng (-2; 8).