100 công thức về giao tuyến của ba mặt phẳng và hệ quả (2024 có đáp án) và cách giải các dạng toán

Công thức Giao tuyến của ba mặt phẳng và hệ quả 

1. Lý thuyết

Định lý:

Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.

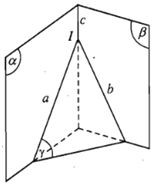
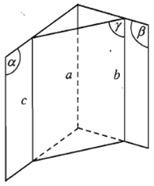
Hệ quả:

Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của hai mặt phẳng đó (nếu có) cũng song song với hai đường thẳng đó (hoặc trùng với một trong hai đường thẳng đó).

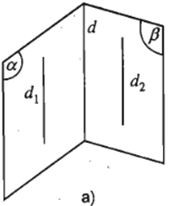
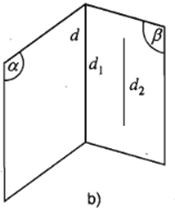
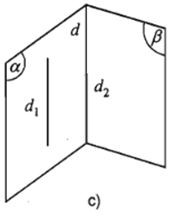
2. Công thức

Phương pháp tìm giao tuyến của hai mặt phẳng chứa hai đường thẳng song song với nhau

Giả sử $a\subset \left(P\right),b\subset \left(Q\right),a//b$. Tìm giao tuyến của (P) và (Q)

Bước 1: Tìm 1 điểm chung M của (P) và (Q)

Bước 2: Ta có: $\left\{\begin{array}{l}M\in \left(P\right)\cap \left(Q\right)\\ a\subset \left(P\right)\\ b\subset \left(Q\right)\\ a//b\end{array}\right.$

Kết luận: Giao tuyến của (P) và (Q) là đường thẳng d, với d đi qua M và d // a // b.

3. Ví dụ minh họa

Ví dụ 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Tìm giao tuyến của các mặt phẳng:

a) (SAB) và (SCD).

b) (MCD) và (SAB), với M là một điểm bất kì thuộc cạnh SA.

Lời giải

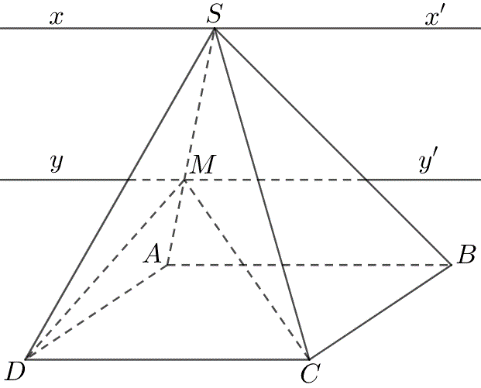
a)

Ta có:$\left\{\begin{array}{l}S\in \left(SAB\right)\cap \left(SCD\right)\\ AB\subset \left(SAB\right)\\ CD\subset \left(SCD\right)\\ AB\text{//}CD\end{array}\right.$

$\Rightarrow \left(SAB\right)\cap \left(SCD\right)=x{x}^{\text{'}}$, với $S\in x{x}^{\text{'}}$ và xx' // AB // CD.

b)

Ta có:$\left\{\begin{array}{l}M\in \left(SAB\right)\cap \left(MCD\right)\\ AB\subset \left(SAB\right)\\ CD\subset \left(MCD\right)\\ AB\text{//}CD\end{array}\right.$

$\Rightarrow \left(SAB\right)\cap \left(SCD\right)=y{y}^{\text{'}}$, với $M\in y{y}^{\text{'}}$ và yy' // AB // CD.

Ví dụ 2: Cho hình chóp S.ABCD có đáy ABCD là hình thang với các cạnh đáy là AB và CD. Gọi I, J lần lượt là trung điểm của các cạnh AD và BC và G là trọng tâm của tam giác SAB.

a) Tìm giao tuyến của hai mặt phẳng (SAB) và (IJG).

b) Xác định thiết diện của mặt phẳng (IJG) với hình chóp.

Lời giải

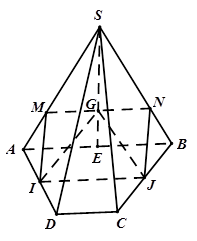
a) Ta có ABCD là hình thang (AB // CD) và I, J là trung điểm của AD, BC

Suy ra IJ là đường trung bình của hình thang ABCD nên IJ // AB.

Ta có: $\left\{\begin{array}{l}G\in \left(SAB\right)\cap \left(IJG\right)\\ AB\subset \left(SAB\right)\\ IJ\subset \left(IJG\right)\\ AB//IJ\end{array}\right.$

$\Rightarrow \left(SAB\right)\cap \left(IJG\right)=d$ với $G\in d$ và d // AB // IJ.

b) Trong (SAB), gọi d cắt SA, SB lần lượt tại M, N.

Ta có:$\left\{\begin{array}{l}\left(IJG\right)\cap \left(ABCD\right)=IJ\\ \left(IJG\right)\cap \left(SBC\right)=JN\\ \left(IJG\right)\cap \left(SAB\right)=NM\\ \left(IJG\right)\cap \left(SAD\right)=MI\end{array}\right.$

Vậy tứ giác IJNM là thiết diện của mặt phẳng (IJG) với hình chóp.

4. Bài tập tự luyện

Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAD)và (SBC). Khẳng định nào sau đây đúng?

A. d qua S và song song với BC.

B. d qua S và song song với DC.

C. d qua S và song song với AB.

D. d qua S và song song với BD.

Câu 2. Cho tứ diện ABCD. Gọi I và J theo thứ tự là trung điểm của AD và AC, G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GIJ) và (BCD) là đường thẳng:

A. qua I và song song với AB.

B. qua J và song song với BD.

C. qua G và song song với CD.

D. qua G và song song với BC.

Đáp án: 1A, 2C