100 công thức về tính GTNN - GTLN của hàm số lượng giác chi tiết (2024 có đáp án) và cách giải các dạng toán

Công thức tính GTNN - GTLN của hàm số lượng giác chi tiết 

1. Lí thuyết

a) Sử dụng tính bị chặn của hàm số lượng giác

$-1\le \sin \left[u\left(x\right)\right]\le 1$; $0\le {\sin }^2\left[u\left(x\right)\right]\le 1$; $0\le \left|\sin \left[u\left(x\right)\right]\right|\le 1$

$-1\le \cos \left[u\left(x\right)\right]\le 1$; $0\le {\cos }^2\left[u\left(x\right)\right]\le 1$; $0\le \left|\cos \left[u\left(x\right)\right]\right|\le 1$

b) Dạng y = asinx + bcosx + c

+ Bước 1: Đưa hàm số về dạng chỉ chứa sin[u(x)] hoặc cos[u(x)]:

y = asinx + bcosx + c$=\sqrt{a^2+b^2}\left(\frac{a}{\sqrt{a^2+b^2}}\sin x+\frac{b}{\sqrt{a^2+b^2}}\cos x\right)+c$

$\iff y=\sqrt{a^2+b^2}.\sin \left(x+\alpha \right)+c$ với $\alpha$ thỏa mãn

$\cos \alpha =\frac{a}{\sqrt{a^2+b^2}};\sin \alpha =\frac{b}{\sqrt{a^2+b^2}}$

+ Bước 2: Đánh giá $-1\le \sin \left(x+\alpha \right)\le 1\forall x\in ℝ$

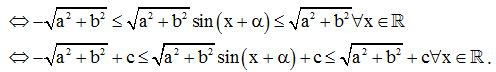
2. Công thức

a) Dạng y = asin[u(x)] + b hoặc y = acos[u(x)] + b

Ta có: $-\left|a\right|+b\le y\le \left|a\right|+b$

Hàm số có giá trị nhỏ nhất là –|a| + b và giá trị lớn nhất là |a| + b.

b) Dạng y = asin2[u(x)] + b ; y = a|sin[u(x)]| + b

Dạng y = acos2[u(x)] + b; y = a|cos[u(x)]| + b (với a khác 0)

+ Trường hợp 1:  a > 0. Ta có: $b\le y\le a+b$.

Hàm số có giá trị nhỏ nhất là b và giá trị lớn nhất là a + b.

+ Trường hợp 2: a < 0. Ta có: $a+b\le y\le b$.

Hàm số có giá trị nhỏ nhất là a + b và giá trị lớn nhất là b.

c) Dạng y = asinx + bcosx + c

Ta có: $-\sqrt{a^2+b^2}+c\le y\le \sqrt{a^2+b^2}+c$

Hàm số có giá trị nhỏ nhất là $-\sqrt{a^2+b^2}+c$ và giá trị lớn nhất là $\sqrt{a^2+b^2}+c$.

3. Ví dụ minh họa

Ví dụ 1: Tìm giá trị lớn nhất và nhỏ nhất của hàm số sau:

a) y = 3sin(2x+1) – 7

b) $y=-2{\cos }^2\left(x+\frac{\pi }{3}\right)+1$

Lời giải

a) y = 3sin(2x+1) – 7

Cách 1: Áp dụng công thức ta có: $-3-7\le y\le 3-7\iff -10\le y\le -4$

Cách 2: Giải chi tiết

Ta có $-1\le \sin \left(2x+1\right)\le 1\forall x\in ℝ$

$\begin{array}{l}\iff -3\le 3\sin \left(2x+1\right)\le 3\forall x\in ℝ\\ \iff -10\le \sin \left(2x+1\right)-7\le -4\forall x\in ℝ\\ \iff -10\le y\le -4\end{array}$

Vậy giá trị lớn nhất của hàm số là -4 và giá trị nhỏ nhất của hàm số là -10.

b) $y=-2{\cos }^2\left(x+\frac{\pi }{3}\right)+1$

Cách 1: Áp dụng công thức ta có: $-2+1\le y\le 1\iff -1\le y\le 1$.

Cách 2: Giải chi tiết

Ta có $0\le {\cos }^2\left(x+\frac{\pi }{3}\right)\le 1\forall x\in ℝ$

$\begin{array}{l}\iff 0\le 2{\cos }^2\left(x+\frac{\pi }{3}\right)\le 2\forall x\in ℝ\\ \iff -2\le -2{\cos }^2\left(x+\frac{\pi }{3}\right)\le 0\forall x\in ℝ\\ \iff -1\le -2{\cos }^2\left(x+\frac{\pi }{3}\right)+1\le 1\forall x\in ℝ\\ \iff -1\le y\le 1\end{array}$

Vậy giá trị lớn nhất của hàm số là 1 và giá trị nhỏ nhất của hàm số là -1.

Ví dụ 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: y = 5sin2x – 12cosx + 2

Lời giải

Cách 1: Áp dụng công thức ta có:

$$\begin{gathered} -\sqrt{5^2+{12}^2}+2\le y\le \sqrt{5^2+{12}^2}+2 \\ \iff -11\le y\le 15 \end{gathered}$$

Cách 2: Giải chi tiết

Ta có: y = 5sin2x – 12cosx + 2

$\begin{array}{l}\iff y=13\left(\frac{5}{13}\sin 2x-\frac{12}{13}\cos 2x\right)+2\\ \iff y=13\left(\sin 2x\cos \alpha -\cos 2x\sin \alpha \right)+2\end{array}$

$\iff y=13\sin \left(2x-\alpha \right)+2$ với $\frac{5}{13}=\cos \alpha ;\frac{12}{13}=\sin \alpha$.

Ta có $-1\le \sin \left(2x-\alpha \right)\le 1\forall x\in ℝ$

$\begin{array}{l}\iff -13\le 13\sin \left(2x-\alpha \right)\le 13\forall x\in ℝ\\ \iff -11\le 13\sin \left(2x-\alpha \right)+2\le 15\forall x\in ℝ\\ \iff -11\le y\le 15\end{array}$

Vậy giá trị lớn nhất của hàm số là 15 và giá trị nhỏ nhất của hàm số là -11.

4. Bài tập tự luyện

Câu 1. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y=7-2\cos \left(x+\frac{\pi }{4}\right)$lần lượt là:

A. 4 và 7

B. -2 và 7

C. 5 và 9

D. -2 và 2

Câu 2. Giá trị nhỏ nhất và lớn nhất của hàm số y = 4cos2x – 3sin2x + 6 là:

A. 3 và 10

B. 1 và 11

C. 6 và 10

D. -1 và 13

Câu 3. Giá trị lớn nhất và nhỏ nhất của hàm số y = 3 – 2|sinx| lần lượt là

A. 1 và 0

B. 3 và 2

C. 3 và -2

D. 3 và 1

Đáp án:

1 – C, 2 – B, 3 – D