100 bài tập về sự đồng biến và nghịch biến của hàm số (2024 có đáp án) và cách giải các dạng toán
Cách giải các dạng toán về sự đồng biến và nghịch biến của hàm số gồm phương pháp giải, ví dụ minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập các dạng toán về sự đồng biến và nghịch biến của hàm số. Mời các bạn đón xem:
Nội dung bài viết
Xem thêm »
Bài tập về sự đồng biến và nghịch biến của hàm số
A. LÝ THUYẾT.
1. Định nghĩa.
Cho hàm số y = f(x) xác định trên K, với K là một khoảng, nửa khoảng hoặc một đoạn.
- Hàm số y = f(x) đồng biến (tăng) trên K nếu ∀ x1, x2 ∈ K, x1 < x2 ⇒ f(x1) < f(x2).
- Hàm số y = f(x) nghịch biến (giảm) trên K nếu ∀ x1, x2 ∈ K, x1 < x2 ⇒ f(x1) > f(x2).
2. Điều kiện cần để hàm số đơn điệu.
Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.
– Nếu hàm số đồng biến trên khoảng K thì f'(x) ≥ 0, ∀ x ∈ K
– Nếu hàm số nghịch biến trên khoảng K thì f'(x) ≤ 0, ∀ x ∈ K.
3. Điều kiện đủ để hàm số đơn điệu.
Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.
– Nếu f'(x) > 0, ∀x ∈ K thì hàm số đồng biến trên khoảng K.
– Nếu f'(x) < 0, ∀x ∈ K thì hàm số nghịch biến trên khoảng K.
– Nếu f'(x) = 0, ∀x ∈ K thì hàm số không đổi trên khoảng K.
Lưu ý
– Nếu f'(x) ≥ 0, ∀x ∈ K (hoặc f'(x) ≤ 0, ∀x ∈ K) và f'(x) = 0 chỉ tại một số điểm hữu hạn của K thì hàm số đồng biến trên khoảng K (hoặc nghịch biến trên khoảng K).
B. CÁC DẠNG TOÁN THƯỜNG GẶP VÀ PHƯƠNG PHÁP GIẢI.
Phần I. Các bài toán không chứa tham số.
Dạng 1: Sử dụng đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số.
1. Phương pháp giải.
Bước 1. Tìm tập xác định D.
Bước 2. Tính đạo hàm y’ = f'(x). Tìm các giá trị xi (i=1, 2, .., n) mà tại đó f'(x) = 0 hoặc f'(x) không xác định.
Bước 4. Sắp xếp các giá trị xi theo thứ tự tăng dần và lập bảng biến thiên.
Bước 5. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số và chọn đáp án chính xác nhất.
2. Ví dụ minh hoạ.
Ví dụ 1. Cho hàm số y=x+3+2√2−x. Khẳng định nào sau đây là khẳng đúng
A. Hàm số đồng biến trên khoảng (−∞;−2) và nghịch biến trên khoảng (−2;2).
B. Hàm số đồng biến trên khoảng (−∞;1) và nghịch biến trên khoảng (1;2).
C. Hàm số nghịch biến trên khoảng (−∞;−2) và đồng biến trên khoảng (−2;2).
D. Hàm số nghịch biến trên khoảng (−∞;1) và đồng biến trên khoảng (1;2).
Lời giải
Tập xác định: D=(−∞;2]
Đạo hàm:
y'
Bảng biến thiên:
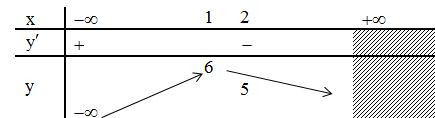
Kết luận: hàm số đã cho đồng biến trên khoảng và nghịch biến trên khoảng (1;2).
Chọn B.
Ví dụ 2. Cho hàm số y = x3 + 3x2 – 9x – 7 . Khẳng định nào sau đây là khẳng định sai?
A. Hàm số nghịch biến trên khoảng (-3;1).
B. Hàm số đồng biến trên (-9;-5).
C. Hàm số đồng biến trên R.
D. Hàm số đồng biến trên
Lời giải
Tập xác định: D=R.
Ta có:
;
Bảng biến thiên:
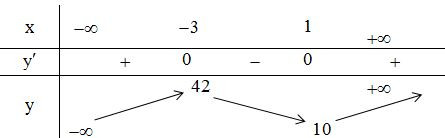
Kết luận: Hàm số đồng biến trên các khoảng: . Hàm số nghịch biến trên khoảng
Chọn C.
Ví dụ 3. Các khoảng nghịch biến của hàm số là
A. và
B. và
C. và
D. và
Lời giải
Tập xác định: D=R
Ta có:
;
Bảng biến thiên
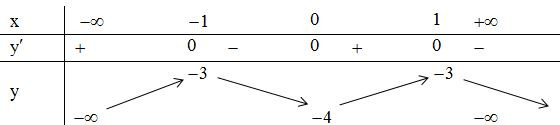
Kết luận: Hàm số đồng biến trên các khoảng: . Hàm số nghịch biến trên các khoảng:
Chọn A.
Ví dụ 4. Chọn mệnh đề đúng về hàm số
A. Hàm số nghịch biến trên từng khoảng xác định của nó.
B. Hàm số đồng biến trên tập xác định của nó.
C. Hàm số đồng biến trên từng khoảng xác định của nó.
D. Hàm số nghịch biến trên tập xác định của nó.
Lời giải
Tập xác định: .Ta có: . Nên hàm số đồng biến trên từng khoảng xác định của nó.
Bảng biến thiên
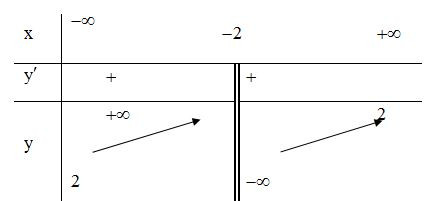
Kết luận: hàm số đồng biến trên từng khoảng xác định.
Chọn C.
Ví dụ 5. Cho hàm số với . Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên .
B. Hàm số nghịch biến trên
C. Hàm số nghịch biến trên .
D. Hàm số nghịch biến trên .
Lời giải
Tập xác định:
Đạo hàm:
Do
Bảng biến thiên
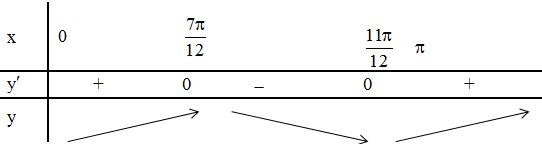
Chọn D.
3. Bài tập tự luyện.
Câu 1. Cho hàm số . Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số luôn nghịch biến trên R.
B. Hàm số nghịch biến trên các khoảng và
C. Hàm số đồng biến trên khoảng và nghịch biến trên khoảng
D. Hàm số luôn đồng biến trên R.
Câu 2. Hỏi hàm số nào sau đây luôn nghịch biến trên R?
A. .
B. .
C. .
D. .
Câu 3. Hỏi hàm số nghịch biến trên các khoảng nào ?
A. và .
B. .
C. và .
D. và .
Câu 4. Hỏi hàm số đồng biến trên khoảng nào?
A. .
B. R.
C. .
D. .
Câu 5. Cho hàm số . Hỏi hàm số luôn đồng biến trên R khi nào?
A.
B.
C.
D.
Câu 6. Cho hàm số . Khẳng định nào sau đây là khẳng định sai?
A. Hàm số đồng biến trên khoảng .
B. Hàm số đồng biến trên các khoảng .
C. Hàm số nghịch biến trên các khoảng .
D. Hàm số nghịch biến trên khoảng .
Câu 7. Cho các hàm số sau:
Có bao nhiêu hàm số đồng biến trên những khoảng mà nó xác định?
A. 2.
B. 4.
C. 3.
D. 5.
Câu 8. Cho các hàm số sau:
Hỏi hàm số nào nghịch biến trên toàn trục số?
A. (I), (II).
B. (I), (II) và (III).
C. (I), (II) và (IV).
D. (II), (III).
Câu 9. Xét các mệnh đề sau:
(I). Hàm số nghịch biến trên R.
(II). Hàm số đồng biến trên tập xác định của nó.
(III). Hàm số đồng biến trên R.
Hỏi có bao nhiêu mệnh đề đúng?
A. 3.
B. 2.
C. 1.
D. 0.
Câu 10. Cho hàm số . Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số nghịch biến trên khoảng và đồng biến trên khoảng .
B. Hàm số đồng biến trên khoảng và nghịch biến trên khoảng .
C. Hàm số đồng biến trên khoảng và nghịch biến trên khoảng .
D. Hàm số nghịch biến trên khoảng và đồng biến trên khoảng .
Câu 11. Hàm số . Chọn phát biểu đúng:
A. Luôn đồng biến trên R.
B. Luôn nghịch biến trên từng khoảng xác định.
C. Đồng biến trên từng khoảng xác định.
D. Luôn nghịch biến trên R.
Câu 12. Cho hàm số . Khoảng đồng biến của hàm số này là
A.
B.
C.
D. (0; 2).
Câu 13. Cho hàm số: . Trong các mệnh đề sau, tìm mệnh đề sai:
A. f(x) nghịch biến trên khoảng (5;10).
B. f(x) giảm trên khoảng (-1;3).
C. f(x) nghịch biến trên khoảng (-3;-1).
D. f(x) đồng biến trên khoảng (-1;1).
Câu 14. (ĐỀ THI THPT QUỐC GIA NĂM 2017). Hàm số nào đồng biến trên khoảng :
A. .
B. .
C. .
D. .
Câu 15. Tập xác định của hàm số là:
A. D = R\{-1}.
B. D = R.
C. R\{2}.
D. D = R\{0}.
Câu 16. Khẳng định nào sau đây sai?
A. Hàm số luôn đồng biến trên R.
B. Hàm số luôn nghịch biến trên R.
C. Hàm số luôn đồng biến trên mỗi khoảng xác định.
D. Hàm số luôn nghịch biến trên (-∞;0).
Câu 17. Cho hàm số . Hàm số nghịch biến trên khoảng nào dưới đây?
A. (0;2).
B. (0;1).
C. (1;2).
D. (-1;1).
Câu 18. Hàm số nào sau đây đồng biến trên R?
A. .
B. .
C. .
D. .
Câu 19. Cho . Hãy chọn mệnh đề sai trong bốn phát biểu sau:
A. Hàm số nghịch biến trên các khoảng ( -∞; -1) và (0;1).
B. Hàm số đồng biến trên các khoảng (-∞;-1) và (1;+ ∞).
C. Trên các khoảng (-∞;-1) và (0;1), y’ < 0 nên hàm số nghịch biến.
D. Trên các khoảng (-1;0) và (1;+ ∞), y’ > 0 nên hàm số đồng biến.
Câu 20. (ĐỀ THPT QG 2017) Hàm số nào sau đây đồng biến trên R.
A. .
B. 2.
C. .
D. y = 2x + 3.
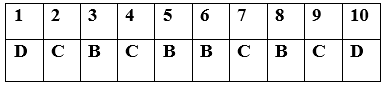
Đáp án

Dạng 2: Từ bảng biến thiên, đồ thị hàm số của hàm số f’(x), xác định khoảng đồng biến, nghịch biến của hàm số đã cho.
1. Phương pháp giải.
- Dựa vào bảng biến thiên có sẵn, kết luận khoảng đồng biến, nghịch biến và chọn đáp án đúng.
- Từ đồ thị hàm số của hàm số f’(x), ta có:
+ Khoảng đồng biến của hàm số là khoảng mà tại đó giá trị f'(x) > 0 (nằm phía trên trục hoành).
+ Khoảng đồng biến của hàm số là khoảng mà tại đó f'(x) < 0 (nằm phía dưới trục hoành).
Xét bài toán: Cho bảng biến thiên của hàm số f’(x). Xét tính đồng biến, nghịch biến của hàm số g(x) theo f(x).
- Các bước giải:
Bước 1: Ta tính đạo hàm.
Bước 2: Kết hợp các nguyên tắc xét dấu tích, thương, tổng (hiệu) và bảng biến thiên của f’(x) để có được bảng xét dấu cho .
Bước 3: Dựa vào bảng xét dấu của vừa có để kết luận về sự đồng biến, nghịch biến của hàm số g(x).
2. Ví dụ minh hoạ.
Ví dụ. Cho hàm số y = f(x) có bảng biến thiên như hình bên. Hàm số y = -2018.f(x) đồng biến trên khoảng nào dưới đây?
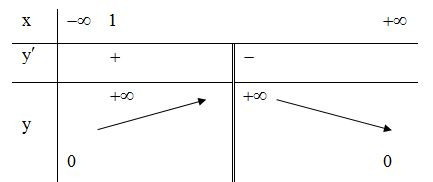
A.
B.
C.
D.
Lời giải
Đặt ,
ta có: .
Xét
Vậy hàm số đồng biến trn khoảng
Chọn B.
3. Bài tập tự luyện.
Câu 1. Cho hàm số có đạo hàm liên tục trên và hàm số có đồ thị như hình vẽ bên dưới.
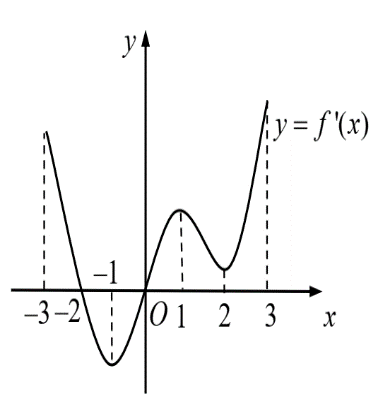
Hàm số nghịch biến trên khoảng nào?
A.
B.
C.
D.
Câu 2. Cho hàm số f(x) có bảng biến thiên như sau:
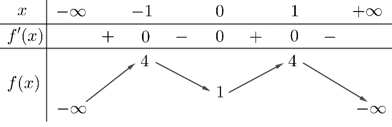
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. .
B. .
C. .
D. .
Câu 3. Cho hàm số . Biết có đạo hàm là và hàm số có đồ thị như hình vẽ bên.
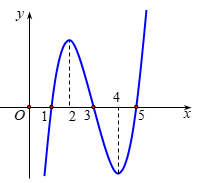
Kết luận nào sau đây là đúng?
A. Hàm số y = f(x) chỉ có hai điểm cực trị.
B. Hàm số y = f(x) đồng biến trên khoảng .
C. Hàm số y = f(x) đồng biến trên khoảng .
D. Hàm số y = f(x) nghịch biến trên khoảng .
Câu 4. Cho hàm số f(x) xác định trên R và có đồ thị của hàm số f '(x) như hình vẽ.
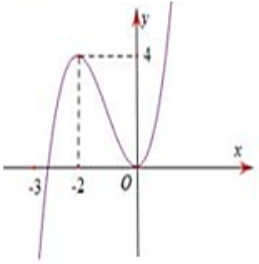
Mệnh đề nào sau đây đúng?
A. Hàm số y = f(x) đồng biến trên khoảng .
B. Hàm số y = f(x) nghịch biến trên khoảng
C. Hàm số y = f(x) đồng biến trên khoảng
D. Hàm số y = f(x) nghịch biến trên khoảng
Câu 5. Cho hàm số f(x) xác định trên R và có đồ thị của hàm số f '(x) như hình vẽ.
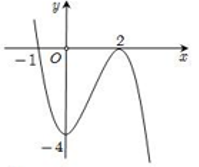
Mệnh đề nào sau đây đúng?
A. Hàm số y = f(x) đồng biến trên khoảng
B. Hàm số y = f(x) đồng biến trên khoảng
C. Hàm số y = f(x) đồng biến trên khoảng
D. Hàm số y = f(x) nghịch biến trên khoảng và
Câu 6. Cho hàm số f(x) có đạo hàm f '(x) xác định, liên tục trên R và f '(x) có đồ thị như hình vẽ bên.
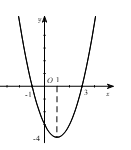
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên
B. Hàm số đồng biến trên và
C. Hàm số nghịch biến trên
D. Hàm số đồng biến trên
Câu 7. Cho hàm số f(x) có đạo hàm f '(x) xác định, liên tục trên R và f '(x) có đồ thị như hình vẽ bên.
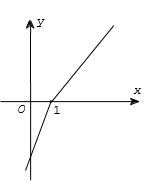
Khẳng định nào sau đây là đúng?
A. Hàm số f(x) đồng biến trên
B. Hàm số f(x) đồng biến trên và
C. Hàm số f(x) đồng biến trên
D. Hàm số f(x) đồng biến trên
Câu 8. Cho hàm số . Biết rằng hàm số có đạo hàm là và hàm số có đồ thị như hình vẽ bên.
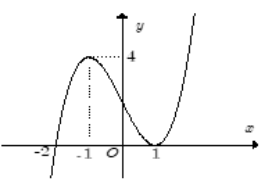
Khi đó nhận xét nào sau đây là sai?
A. Trên thì hàm số luôn tăng.
B. Hàm giảm trên đoạn .
C. Hàm đồng biến trên khoảng .
D. Hàm nghịch biến trên khoảng
Câu 9. Cho hàm số liên tục và xác định trên R. Biết có đạo hàm và hàm số có đồ thị như hình vẽ:
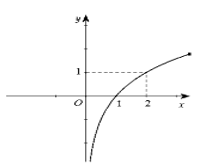
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên R
B. Hàm số nghịch biến trên R
C. Hàm số chỉ nghịch biến trên khoảng (0;1)
D. Hàm số đồng biến trên khoảng .
Câu 10. Cho hàm số y = f(x) có bảng biến thiên như sau
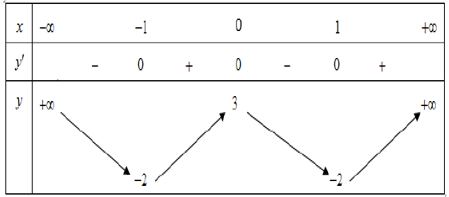
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. (-1;0)
B. (-∞;0)
C. (1;+∞)
D. (0;1)
Đáp án
Dạng 3. Xét sự đồng biến, nghịch biến của hàm hợp.
1. Phương pháp giải.
Bài toán 1: Cho hàm y = f(x) hoặc hàm y = f '(x) xét sự biến thiên của hàm g(x) = f(u(x)).
Phương pháp:
- Tính đạo hàm
- Xét dấu dựa vào dấu của và theo quy tắc nhân dấu. Lưu ý khi xét dấu dựa vào dấu của như sau: Nếu không đổi dấu trên D thì không đổi dấu khi .
Bài toán 2: Cho hàm y = f(x) hoặc y = f '(x) xét sự biến thiên của hàm g(x) = f(u(x))+h(x).
Phương pháp:
- Tính
- Lập bảng xét dấu bằng cách cộng dấu của hai biểu thức và .
Bài toán 3: Cho hàm y = f(u(x)) hoặc hàm y = f '(u(x)) xét sự biến thiên của hàm y = f(x).
Phương pháp: Giả sử ta có: . Ta cần giải BPT .
- Đặt
- Giải bất phương trình:
- Vậy .
2. Ví dụ minh hoạ.
Ví dụ 1. Cho hàm số có đạo hàm trên R. Hàm số có đồ thị như hình vẽ:
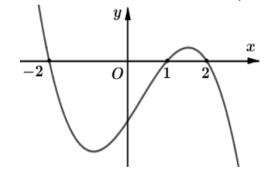
Hàm số đồng biến trên khoảng nào dưới đây?
A. .
B. .
C. .
D. .
Lời giải
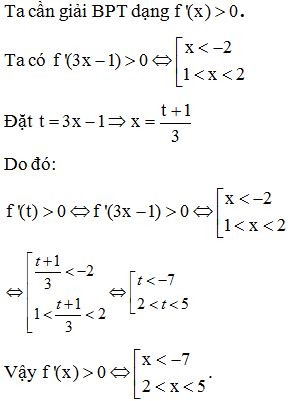
Chọn B.
Ví dụ 2. Cho hàm số , bảng xét dấu của như sau:

Hàm số nghịch biến trên khoảng nào dưới đây?
A. (2;3).
B. (0;2).
C. (3;5).
D. (5;+∞).
Lời giải
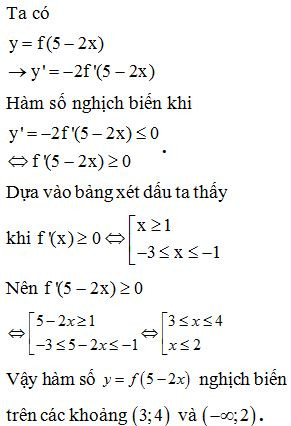
Chọn B
Ví dụ 3. Cho hàm số có đạo hàm trên R và có đồ thị hàm như hình vẽ dưới đây. Hàm số đồng biến trên khoảng nào?
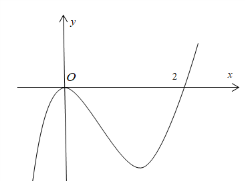
A. .
B. .
C. .
D. .
Lời giải
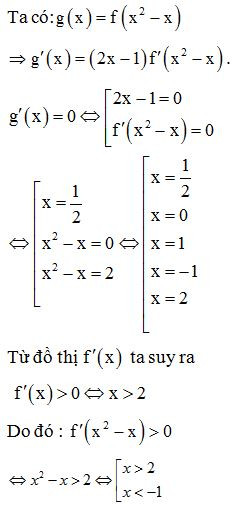
(Ta cần xác định một loại dấu của )
Bảng xét dấu :

Từ bảng xét dấu ta có hàm số g(x) đồng biến trên khoảng .
Chọn C.
Lưu ý: Dấu của ở bảng trên có được nhờ nhân dấu của hai biểu thức và .
Ví dụ 4. Cho hàm số có bảng xét dấu của đạo hàm như sau:
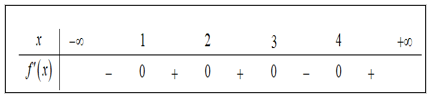
Hàm số đồng biến trên khoảng nào dưới đây?
A. .
B. .
C. .
D. .
Lời giải
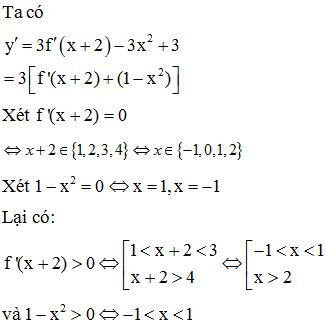
Bảng xét dấu
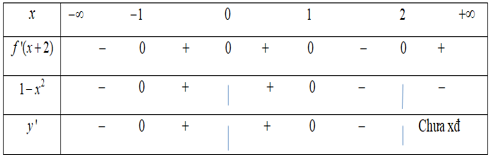
Từ bảng xét dấu suy ra trên khoảng hàm số đồng biến.
Chọn C.
Ví dụ 5. Cho hàm số có . Hàm số nghịch biến trên khoảng nào sau đây.
A. .
B. .
C. .
D. .
Lời giải
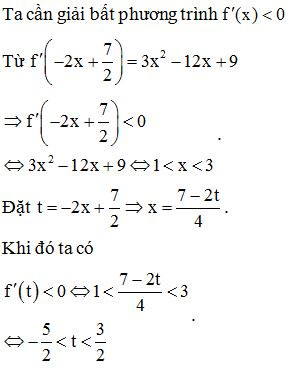
Vậy hàm số f(x) nghịch biến trên khoảng
Chọn C.
3. Bài tập tự luyện.
Bài 1. Cho hàm số có đạo hàm liên tục trên R. Đồ thị hàm số như hình vẽ. Hàm số nghịch trên khoảng nào?
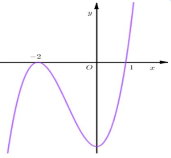
A.
B.
C.
D.
Bài 2. Cho hàm số có đồ thị hàm số như hình vẽ bên. Hỏi hàm số đồng biến trên khoảng nào sau đây?
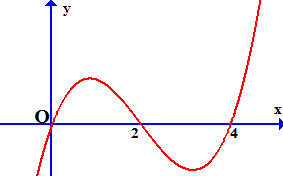
A.
B.
C.
D.
Bài 3. Cho hàm số có đạo hàm trên R. Đồ thị hàm số như hình vẽ bên dưới.
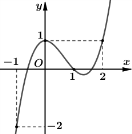
Hàm số đồng biến trên khoảng nào trong các khoảng sau?
A. .
B. .
C. .
D.
Bài 4. (Đề tham khảo BGD năm 2017-2018) Cho hàm số . Hàm số có đồ thị như hình bên. Hàm số đồng biến trên khoảng:
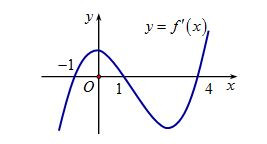
A. .
B. .
C. .
D. .
Bài 5. (Sở GD&ĐT Nam Định năm 2018-2019) Cho hàm số f(x) liên tục trên và có đạo hàm f’(x) thỏa mãn f’(x) = (1-x)(x+2)g(x) + 2018 với g(x) < 0, . Hàm số y = f(1-x) + 2018x + 2019 nghịch biến trên khoảng nào?
A. (1;+∞)
B. (0;3)
C. (-∞;3)
D. (4;+∞)
Bài 6. Cho hàm số f '(x) có bảng xét dấu như sau:

Hàm số nghịch biến trên khoảng nào dưới đây?
A.
B.
C.
D.
Bài 7. Cho hàm số . Biết hàm số có đồ thị như hình vẽ bên. Hàm số đồng biến trong khoảng nào dưới đây?
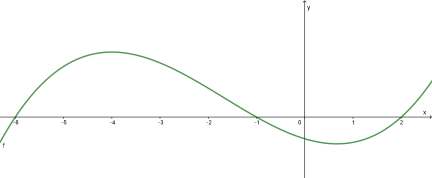
A.
B.
C.
D.
Bài 8. Cho hàm số liên tục trên R, hàm số có đồ thị như hình vẽ. Xét hàm số . Hãy chọn khẳng định đúng:
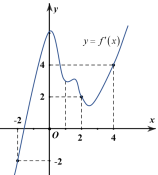
A. Hàm số h(x) nghịch biến trên R
B. Hàm số h(x) nghịch biến trên
C. Hàm số h(x) đồng biến trên
D. Hàm số h(x) đồng biến trên R
Bài 9. (Chuyên Quốc Học Huế năm 2018-2019) Cho hàm số f(x) có đạo hàm trên là f’(x) = (x-1)(x+3). Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10;20] để hàm số y = f(x2+3x-m) đồng biến trên khoảng (0;2)?
A. 18
B. 17
C. 16
D. 20
Bài 10. Cho hàm số có đồ thị của hàm số như hình vẽ.
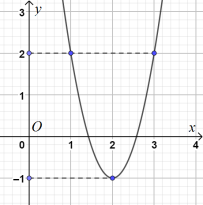
Hỏi hàm số nghịch biến trên khoảng nào dưới đây?
A.
B.
C.
D.
Đáp án

Phần II. Các bài toán có chứa tham số.
Dạng 4. Tìm tham số m để hàm số đồng biến (nghịch biến) tập xác định (khoảng xác định) của hàm số.
1. Phương pháp giải.
Bài toán 1. Tìm tham số m để hàm số đơn điệu trên
Bước 1: Tập xác định: D=R
Bước 2: Đạo hàm
Bước 3: Điều kiện đơn điệu (khi ).
- Hàm số đồng biến trên
- Hàm số nghịch biến trên
Lưu ý: Nếu hàm bậc ba có a chứa tham số thì ta cần xét a=0 để kiểm tra xem hàm số có đơn điệu trên R hay không.
- Không xét bài toán tìm m để hàm số đơn điệu trên R do phương trình y’=0 luôn có ít nhất 1 nghiệm là x = 0.
Bài toán 2. Tìm tham số m để hàm số () đơn điệu trên mỗi khoảng xác định của nó.
Phương pháp:
Bước 1: Tập xác định:
Bước 2: Đạo hàm:
Bước 3: Điều kiện đơn điệu:
- Hàm số đồng biến trên mỗi khoảng xác định
- Hàm số nghịch biến trên mỗi khoảng xác định
Lưu ý: Nếu hàm số có c chứa tham số thì ta nên xét c=0 để kiểm tra xem hàm số có đơn điệu trên từng khoảng xác định của nó hay không.
Mở rộng:
* Tìm tham số để hàm số () đơn điệu trên mỗi khoảng xác định của nó.
Phương pháp:
Bước 1: Tập xác định:
Bước 2: Đạo hàm: với
,
Bước 3: Điều kiện đơn điệu
- Hàm số đồng biến trên mỗi khoảng xác định
- Hàm số nghịch biến trên mỗi khoảng xác định
Lưu ý: Nếu gặp câu hỏi tương tự dành cho hàm số thì ta cũng làm theo phương pháp nêu trên.
- Đối với bài toán 2, đạo hàm chỉ lớn hơn 0 hoặc nhỏ hơn 0 chứ không được cho Lý do là nếu ta cho y'=0 thì sẽ có vô số giá trị x thỏa mãn (mà định nghĩa nêu rõ y'=0 tại một số hữu hạn điểm x mà thôi).
* Tìm tham số m để hàm số lượng giác đơn điệu trên R
Cách 1.
- Tính đạo hàm , cho nếu đề bài yêu cầu hàm số đồng biến trên (Ngược lại: nếu đề bài yêu cầu hàm số nghịch biến trên R)
- Cô lập m để có được dạng
(hoặc ).
- Tìm Max-Min cho hàm số trên R (Hoặc lập bảng biến thiên cho hàm ).
- Dựa vào giá trị Max-Min hoặc bảng biến thiên để kết luận về điều kiện của m.
Cách 2. Đặt (hoặc ) với điều kiện
Bất phương trình:
Hoàn toàn tương tự:
2. Ví dụ minh hoạ.
Ví dụ 1. Cho hàm số với m là tham số. Có bao nhiêu giá trị nguyên của để hàm số nghịch biến trên khoảng
A. 4
B. 6
C. 7
D. 5
Lời giải

Chọn C.
Sai lầm hay gặp là Để hàm số đã cho nghịch biến trên khoảng thì . Khi đó ra giải ra và chọn D.
Ví dụ 2. Hàm số (m là tham số) nghịch biến trên mỗi khoảng xác định của nó khi các giá trị của m là:
A. .
B. .
C. .
D. .
Lời giải
Tập xác định:
Đạo hàm:
Hàm số nghịch biến trên mỗi khoảng xác định của nó khi và chỉ khi
(Dấu chỉ xảy ra tại hữu hạn điểm trên )
Do a = -1 < 0, nên g(x) ≤ 0
Chọn C.
3. Bài tập tự luyện.
Câu 1. Hàm số y = x3 + mx đồng biến trên R khi:
A. Chỉ khi m = 0.
B. Chỉ khi m ≥ 0.
C. Chỉ khi m ≤ 0.
D. Với mọi m.
Câu 2. Tìm m lớn nhất để hàm số đồng biến trên R?
A. m = 1.
B. m = 2.
C. Đáp án khác.
D. m = 3.
Câu 3. Hàm số luôn đống biến trên R thì giá trị m nhỏ nhất là:
A. m = - 4.
B. m = 0.
C. m = - 2.
D. m = 1.
Câu 4. Hàm số nghịch biến trên R thì điều kiện của m là:
A. m > 1.
B. m = 2.
C. m ≤ 1.
D. m ≥ 2.
Câu 5. Hàm số nghịch biến trên thì:
A. m < - 2.
B. m > - 2.
C. m ≤ -2.
D. m ≥ - 2.
Câu 6. Cho hàm số . Khẳng định nào sau đây là đúng?
A. Hàm số luôn nghịch biến.
B. Hàm số luôn đồng biến.
C. Hàm số không đơn điệu trên R
D. Các khẳng định A, B, C đều sai.
Câu 7. Tìm điều kiện của a, b để hàm số luôn luôn đồng biến trên R.
A. .
B. .
C. .
D. .
Câu 8. Giá trị của để hàm số nghịch biến trên toàn trục số là:
A. .
B. .
C. .
D. .
Câu 9. Nếu hàm số nghịch biến thì giá trị của m là:
A. .
B. .
C. .
D. .
Câu 10. Tìm tất cả các giá trị thực của tham số và sao cho hàm số luôn giảm trên R?
A. và
B. và
C. và
D. và
Câu 11. Tìm mối liên hệ giữa các tham số và sao cho hàm số luôn tăng trên R?
A. .
B. .
C. .
D. .
Câu 12. Tìm tất cả các giá trị thực của tham số sao cho hàm số giảm trên các khoảng mà nó xác định ?
A.
B.
C.
D.
Câu 13. Tìm tất cả các giá trị thực của tham số sao cho hàm số sau luôn nghịch biến trên R?
A. .
B .
C. .
D. .
Câu 14. Tìm tất cả các giá trị thực của tham số m sao cho hàm số tăng trên từng khoảng xác định của nó?
A. .
B. .
C. .
D. .
Câu 15. Tìm tất cả các giá trị thực của tham số m sao cho hàm số luôn đồng biến trên R?
A. .
B. .
C. .
D. .
Câu 16. Tìm tất cả các giá trị thực của tham số m sao cho hàm số sau luôn đồng biến trên R?
A. 0.
B. –1.
C. 2.
D. 1.
Câu 17. Tìm số nguyên m nhỏ nhất sao cho hàm số luôn nghịch biến trên các khoảng xác định của nó?
A.
B.
C.
D. Không có m
Câu 18. Hỏi có bao nhiêu giá trị nguyên của tham số m sao cho hàm số đồng biến trên từng khoảng xác định của nó?
A. 2.
B. 4.
C. Vô số.
D. Không có.
Đáp án

Dạng 5. Tìm m để hàm số đồng biến (nghịch biến) trên một khoảng xác định K cho trước.
Bài toán 1. Tìm tham số m để hàm số bậc ba, bậc bốn,… đơn điệu trên tập K cho trước (với là khoảng, đoạn hoặc nửa khoảng).
Phương pháp:
Bước 1: Tìm đạo hàm của hàm .
Bước 2: Điều kiện đơn điệu:
- Hàm số đồng biến trên K
- Hàm số nghịch biến trên K
Bước 3:

*Tìm tham số để hàm số đơn điệu trên một khoảng có độ dài p.
Phương pháp:
Bước 1: Đạo hàm
Bước 2:
- Hàm số đồng biến trên khoảng có độ dài py' có hai nghiệm phân biệt thỏa mãn .
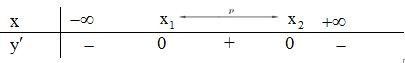
- Hàm số nghịch biến trên khoảng có độ dài py' có hai nghiệm phân biệt thỏa mãn .

Lưu ý:
- Dạng này không cần điều kiện vì điều kiện đã bao hàm hai ý trên.
- Điều kiện có thể được xử lý theo hai cách chính:
+ Một là sử dụng định lí Vi-ét:
+ Hai là tự xây dựng công thức:
Các câu hỏi: “đồng biến (nghịch biến) trên khoảng có độ dài ” ta cũng sẽ làm tương tự.
Bài toán 2. Bài toán tham số đối với những dạng hàm số khác.
Phương pháp:
Bước 1: Tìm đạo hàm của hàm .
Bước 2: Điều kiện đơn điệu:
- Hàm số đồng biến trên
- Hàm số nghịch biến trên
Bước 3:
- Biến đổi theo dạng (hoặc ).
- Lập bảng biến thiên của hàm số g(x) với mọi .
Dựa vào bảng biến thiên và kết luận điều kiện cho tham số
- Giả sử hàm g(x) tồn tại Max-Min trên R. Ta có:
- Nếu hàm g(x) không tồn tại Max-Min trên R, tuy nhiên thông qua bảng biến thiên ta tìm được điều kiện bị chặn: , khi đó:
Bài toán 3: Tìm tham số m để hàm số nhất biến đơn điệu trên một khoảng K cho trước (với là khoảng, đoạn hoặc nửa khoảng).
Phương pháp:
Bước 1: Tập xác định:
Bước 2: Đạo hàm
Bước 3: Điều kiện đơn điệu:
- Hàm số đồng biến trên K
- Hàm số nghịch biến trên K
* Tìm tham số m để hàm số đơn điệu trên khoảng K cho trước.

2. Ví dụ minh hoạ.
Ví dụ 1. (Đề tốt nghiệp 2020-Đợt 2 Mã đề 103) Tập hợp tất cả các giá trị thực của tham số để hàm số đồng biến trên khoảng là:
A.
B.
C.
D. .
Lời giải
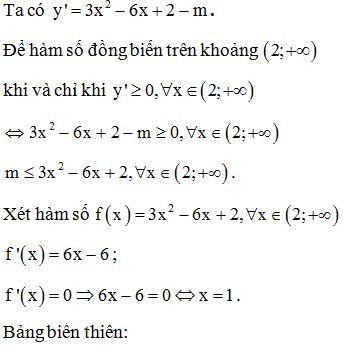
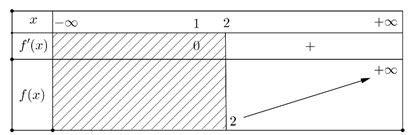
Từ bảng biến thiên ta thấy . Vậy
Chọn D.
Ví dụ 2. (Đề tốt nghiệp THPT 2020 mã đề 103) Tập hợp tất cả các giá trị thực của tham số m để hàm số đồng biến trên khoảng
A. .
B.
C.
D.
Lời giải

Ví dụ 3. (Đề Minh họa lần 1, 2017, BGD) Tìm tất cả các giá trị của m để hàm số đồng biến trên
A.
B. hoặc
C.
D. .
Lời giải
Điều kiện:
Tính đạo hàm nhanh bằng phương pháp sau:

Ta có
(**)
Từ (*) và (**) suy ra
Chọn B.
Ví dụ 4. Tìm tất cả giá trị thực của m để hàm số có độ dài khoảng nghịch biến đúng bằng
A.
B.
C.
D.
Lời giải
Đạo hàm
Hàm số có độ dài khoảng nghịch biến đúng bằng có hai nghiệm phân biệt thỏa mãn :
Chọn A.
3. Bài tập tư luyện.
Câu 1. (Đề tốt nghiệp 2020-Đợt 1 Mã đề 101) Tập hợp tất cả các giá trị thực của tham số để hàm số đồng biến trên khoảng là
A.
B.
C.
D. .
Câu 2. (Đề tốt nghiệp THPT 2020 mã đê 102) Tập hợp tất cả các giá trị thực của tham số m để hàm số đồng biến trên khoảng (-∞;-8) là
A. (5;+∞).
B. (5;8].
C. [5;8).
D. (5;8).
Câu 3. Tìm tất cả các giá trị thực của tham số sao cho hàm số giảm trên khoảng m ?
A. .
B. .
C. .
D. .
Câu 4. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đồng biến trên khoảng ?
A. .
B. .
C. .
D. .
Câu 5. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đồng biến trên khoảng ?
A. .
B. .
C. .
D.
Câu 6. Tìm tất cả các giá trị thực của tham số m sao cho hàm số nghịch biến trên một đoạn có độ dài là 3?
A. .
B. .
C. .
D. .
Câu 7. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đồng biến trên khoảng ?
A. .
B.
C.
D. .
Câu 8. Tìm tất cả các giá trị thực của tham số m sao cho hàm số giảm trên nửa khoảng ?
A. .
B. .
C. .
D. .
Câu 9. Tất cả các giá trị thực của tham số m sao cho hàm số nghịch biến trên khoảng (1;2) là , trong đó phân số tối giản và q >0. Hỏi tổng p+q là?
A. 5.
B. 9.
C. 7.
D. 3.
Câu 10. Hỏi có bao nhiêu giá trị nguyên dương của tham số m sao cho hàm số đồng biến trên khoảng ?
A. 3.
B. 1.
C. 2.
D. 0.
Câu 11. Hàm số đồng biến trên miền [2;+∞) khi:
A. .
B. .
C. .
D. .
Câu 12. Tập tất cả các giá trị của m để hàm số đồng biến trên khoảng (0;3) là:
A. m = 0.
B. .
C. .
D. m tùy ý.
Câu 13. Biết rằng hàm số nghịch biến trên (x1, x2) và đồng biến trên các khoảng còn lại của tập xác định. Nếu thì giá trị m là:
A. -1.
B. 3.
C. - 3 hoặc 1.
D. - 1 hoặc 3.
Câu 14. Giá trị của m để hàm số giảm trên đoạn có độ dài bằng 1 là:
A. .
B. .
C. .
D. .
Câu 15. Hàm số đồng biến trên (1;3) khi:
A. .
B. .
C. .
D. .
Câu 16. Hàm số nghịch biến trên khoảng (-∞;2) khi và chỉ khi:
A. m > 2.
B. m ≥ 1.
C. m ≥ 2.
D. m > 1.
Câu 17. Hàm số nghịch biến trên (-1; +∞) khi:
A. m < 1.
B. m > 2.
C. 1≤m < 2.
D.- 1 < m < 2.
Câu 18. Tìm tất cả giá trị thực của tham số m sao cho hàm số đồng biến trên khoảng .
A. hoặc .
B. .
C. .
D. .
Câu 19. Tìm các giá trị của tham số để hàm số đồng biến trên .
A. .
B. .
C. .
D. .
Câu 20. Gọi là tập hợp tất cả các giá trị của tham số để hàm số sau đồng biến trên R: . Tổng giá trị của tất cả các phần tử thuộc S bằng
A.
B. .
C. .
D.
Đáp án

Phần III. Bài toán ứng dụng sự đồng biến, nghịch biến của hàm số.
1. Phương pháp giải.
Bài toán 1: Đánh giá các bất đẳng thức hoặc
Phương pháp
Chuyển vế để đưa bất đẳng thức về dạng .
Bước 1: Tính đạo hàm và chứng minh đạo hàm chỉ mang một dấu (âm hoặc dương).
Bước 2: Vận dụng tính chất đơn điệu:
- Nếu hàm f(x) đồng biến trên thì ,
- Ngược lại nếu hàm f(x) nghịch biến trên thì ,
Bài toán 2: Giải phương trình dạng với .
Phương pháp:
Bước 1: Nhận diện hàm đặc trưng để đưa phương trình về dạng với ,
Bước 2: Chứng minh hàm đặc trưng đơn điệu trên D ( luôn âm hoặc luôn dương trên D).
Bước 3: Giải phương trình:
Bài toán 3: Giải phương trình dạng có nghiệm duy nhất
Phương pháp:
Bước 1: Tìm một nghiệm của phương trình (bằng tính nhẩm hoặc nhân lượng liên hợp v.v…).
Bước 2: Tính đạo hàm và chứng minh đạo hàm chỉ mang một dấu (tức là hàm đơn điệu trên miền xác định).
Bước 3: Chứng minh hàm số g(x) là hàm hằng hoặc đơn điệu (ngược lại hàm f(x)). Từ đó khẳng định phương trình đã cho có nghiệm duy nhất
2. Ví dụ minh hoạ.
Ví dụ 1. Cho hàm số có , . Tìm tất cả các giá trị thực của x để .
A.
B.
C.
D.
Lời giải
Ta có: nên hàm số y = f(x) nghịch biến trên R.
Do đó:
Chọn D.
Ví dụ 2. Khi giải phương trình: , ta tìm được nghiệm có dạng với a, b là các số nguyên. Hãy tính .
Lời giải

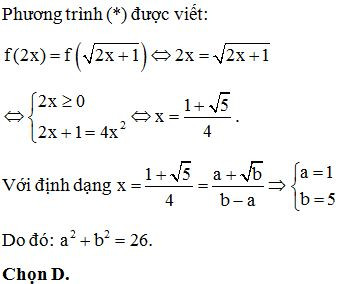
Ví dụ 3. (Đề tốt nghiệp 2020-Đợt 2 Mã đề 103) Cho hàm số f(x) có bảng biến thiên như sau:
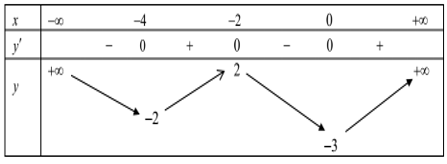
Có bao nhiêu giá trị nguyên của tham số để phương trình có ít nhất ba nghiệm thực phân biệt thuộc khoảng ?
A. 15
B. 12.
C. 14.
D. 13.
Lời giải
Đặt (1)
Ta có BBT sau:
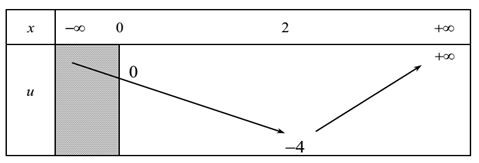



3. Bài tập tự luyện.
Câu 1. Tìm tất cả các giá trị thực của tham số sao cho phương trình có đúng 1 nghiệm?
A. .
B. hoặc .
C. hoặc .
D. .
Câu 2. Tìm tất cả các giá trị thực của tham số m sao cho phương trình có nghiệm thực?
A. .
B. .
C. .
D. .
Câu 3. Tìm tất cả các giá trị thực của tham số m sao cho phương trình có đúng 2 nghiệm dương?
A. .
B. .
C. .
D. .
Câu 4. Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: cũng là nghiệm của bất phương trình ?
A. .
B. .
C. .
D. .
Câu 5. Tìm tất cả các giá trị thực của tham số m sao cho phương trình: có ít nhất một nghiệm trên đoạn ?
A. .
B. .
C. .
D. .
Câu 6. Tìm tất cả các giá trị thực của tham số m sao cho phương trình có hai nghiệm thực?
A. .
B. .
C. .
D. .
Câu 7. Tìm tất cả các giá trị thực của tham số m sao cho phương trình có hai nghiệm thực?
A. .
B. .
C. .
D. .
Câu 8. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình
nghiệm đúng với mọi ?
A. .
B. .
C. .
D. .
Câu 9. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình nghiệm đúng với mọi ?
A. .
B. .
C. .
D.
Câu 10. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình nghiệm đúng ?
A. .
B. .
C. .
D. hoặc .
Câu 11. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình nghiệm đúng ?
A. .
B. .
C. .
D. .
Câu 12. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình: nghiệm đúng ?
A. .
B. .
C. .
D. .
Câu 13. Tìm giá trị lớn nhất của tham số m sao cho bất phương trình có nghiệm?
A. .
B. .
C. .
D. .
Câu 14. Bất phương trình có tập nghiệm là [a,b]. Hỏi tổng a + b có giá trị là bao nhiêu?
A. -2.
B. 4.
C. 5.
D. 3.
Câu 15. Bất phương trình có tập nghiệm . Hỏi hiệu có giá trị là bao nhiêu?
A. 1.
B. 2.
C. 3.
D. -1.
Đáp án
