100 bài tập về phương trình bậc hai đối với hàm số lượng giác (2024 có đáp án) và cách giải các dạng toán

Phương trình bậc hai đối với hàm số lượng giác và cách giải 

1. Lý thuyết

Một số dạng phương trình bậc hai của một hàm số lượng giác

$\begin{array}{l}a.{\sin }^{2}x+b.sinx+c=0,(a\ne 0)\\ a.co{s}^{2}x+b.cosx+c=0,(a\ne 0)\\ a.ta{n}^{2}x+b.tanx+c=0,(a\ne 0)\\ a.co{t}^{2}x+b.cotx+c=0,(a\ne 0)\end{array}$

2. Phương pháp giải

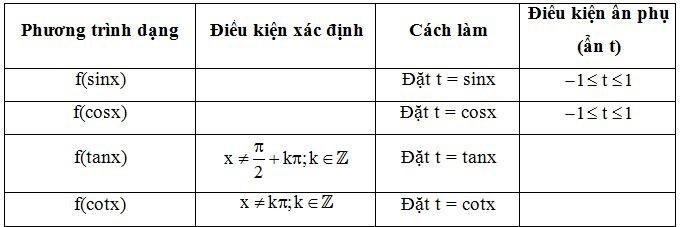
3. Ví dụ minh họa

Ví dụ 1: Giải các phương trình:

a) 2sin2x – 5sinx + 2 = 0

b) 5cos2x – 6cosx + 1 = 0

c) tan2x + 2tanx – 3 = 0

Lời giải

a) Đặt t = sinx với

Ta được phương trình: 2t2 – 5t + 2 = 0

$$\begin{gathered} \iff 2t^2-4t-t+2=0 \\ \iff \left(2t-1\right)\left(t-2\right)=0 \\ \iff \left[\begin{array}{l}t=\frac{1}{2}\\ t=2\left(Loại\right)\end{array}\right. \end{gathered}$$

Khi đó $\sin x=\frac{1}{2}\iff \left[\begin{array}{l}x=\frac{\pi }{6}+k2\pi \\ x=\frac{5\pi }{6}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

Vậy họ nghiệm của phương trình là: $x=\frac{\pi }{6}+k2\pi ;x=\frac{5\pi }{6}+k2\pi ;k\in \mathbb{Z}$.

b) Đặt t = cosx với $-1\le t\le 1$

Ta được phương trình: 5t2 – 6t + 1 = 0

$$\begin{gathered} \iff 5t^2-5t-t+1=0 \\ \iff \left(5t-1\right)\left(t-1\right)=0\iff \left[\begin{array}{l}t=1\\ t=\frac{1}{5}\end{array}\right. \end{gathered}$$(Thỏa mãn)

Khi đó $\left[\begin{array}{l}\cos x=1\\ \cos x=\frac{1}{5}\end{array}\right.\iff \left[\begin{array}{l}x=k2\pi \\ x=\pm \arccos \frac{1}{5}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

Vậy họ nghiệm của phương trình là: $x=k2\pi ;x=\pm \arccos \frac{1}{5}+k2\pi ;k\in \mathbb{Z}$.

c) Điều kiện xác định: $\cos x\ne 0\iff x\ne \frac{\pi }{2}+k\pi ;k\in \mathbb{Z}$.

Đặt t = tanx. Ta được phương trình: t2 + 2t – 3 = 0

$$\begin{gathered} \iff t^2+3t-t-3=0 \\ \iff \left(t+3\right)\left(t-1\right)=0\iff \left[\begin{array}{l}t=-3\\ t=1\end{array}\right. \end{gathered}$$

Khi đó $\iff \left[\begin{array}{l}\tan x=-3\\ \tan x=1\end{array}\right.$$\iff \left[\begin{array}{l}x=\arctan \left(-3\right)+k\pi \\ x=\frac{\pi }{4}+k\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$ (Thỏa mãn điều kiện xác định)

Vậy họ nghiệm của phương trình là: $x=\frac{\pi }{4}+k\pi ;x=\arctan \left(-3\right)+k\pi ;k\in \mathbb{Z}$.

Ví dụ 2: Giải các phương trình:

a) sin2x + 2cosx + 2 = 0

b) cos2x – 4sinx = 3

c) $cos2x–3cosx+4{\cos }^2\frac{x}{2}=0$

Lời giải

a) sin2x + 2cosx + 2 = 0

$\begin{array}{l}\iff 1-{\cos }^{2}x+2cosx+2=0\\ \iff -{\cos }^{2}x+2cosx+3=0\end{array}$

Đặt t = cosx với $-1\le t\le 1$

Ta được phương trình: - t2 + 2t + 3 = 0

$\begin{array}{l}\iff -\left(t+1\right)\left(t-3\right)=0\\ \iff \left[\begin{array}{l}t=-1\\ t=3\left(Loại\right)\end{array}\right.\end{array}$

Khi đó $\cos x=-1\iff x=\pi +k2\pi \left(k\in \mathbb{Z}\right)$

Vậy họ nghiệm của phương trình là: $x=\pi +k2\pi ;k\in \mathbb{Z}$.

b) cos2x – 4sinx = 3

$\begin{array}{l}\iff 1-2{\sin }^{2}x-4\sin x-3=0\\ \iff -2{\sin }^{2}x-4\sin x-2=0\end{array}$

Đặt t = sinx với $-1\le t\le 1$

Ta được phương trình: -2t2 – 4t – 2 = 0

$\iff -2{\left(t+1\right)}^2=0$

$\iff t=-1$ (Thỏa mãn)

Khi đó: $\sin x=-1\iff x=-\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$

Vậy họ nghiệm của phương trình là: $x=-\frac{\pi }{2}+k2\pi ;k\in \mathbb{Z}$.

c) $cos2x–3cosx+4{\cos }^2\frac{x}{2}=0$

$\begin{array}{l}\iff 2{\cos }^{2}x-1-3\cos x+4.\frac{1+\cos x}{2}=0\\ \iff 2{\cos }^{2}x-\cos x+1=0\end{array}$

Đặt t = cosx với $-1\le t\le 1$

Ta được phương trình: 2t2 – t + 1 = 0 (*)

Ta có: $\Delta ={\left(-1\right)}^2-\mathrm{4.2.1}=-7<0$. Do đó phương trình (*) vô nghiệm

Vậy phương trình đã cho vô nghiệm.

Ví dụ 3: Giải các phương trình:

a) tanx + 5cotx = 6

b) $\frac{1}{\sin x}+3{\cot }^{2}x+1=0$

Lời giải

a) Điều kiện xác định:

$$\begin{gathered} \left\{\begin{array}{l}\sin x\ne 0\\ \cos x\ne 0\end{array}\right.\iff \left\{\begin{array}{l}x\ne k\pi \\ x\ne \frac{\pi }{2}+k\pi \end{array}\right. \\ \iff x\ne \frac{k\pi }{2};k\in \mathbb{Z} \end{gathered}$$.

Ta có: tanx + 5cotx = 6$\iff \tan x+\frac{5}{\tan x}=6$

Đặt t = tanx. Ta được phương trình: $t+\frac{5}{t}=6$ (Điều kiện: $t\ne 0$)

$\Rightarrow t^2+5=6t\iff t^2-6t+5=0\iff \left[\begin{array}{l}t=1\\ t=5\end{array}\right.$

Khi đó $\left[\begin{array}{l}\tan x=1\\ \tan x=5\end{array}\right.\iff \left[\begin{array}{l}x=\frac{\pi }{4}+k\pi \\ x=\arctan 5+k\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

Vậy họ nghiệm của phương trình là: $x=\frac{\pi }{4}+k\pi ;x=\arctan 5+k\pi ;k\in \mathbb{Z}$.

b) Điều kiện xác định: $\sin x\ne 0\iff x\ne k\pi ;k\in \mathbb{Z}$

Vì $\frac{1}{{\sin }^{2}x}=1+{\cot }^{2}x$ nên ${\cot }^{2}x=\frac{1}{{\sin }^{2}x}-1$

Thay vào phương trình ta có: $\frac{1}{\sin x}+3\left(\frac{1}{{\sin }^{2}x}-1\right)+1=0$

$\iff 3\frac{1}{{\sin }^{2}x}+\frac{1}{\sin x}-2=0$

Đặt $t=\frac{1}{\sin x}$ (Vì $-1\le \sin x\le 1;\sin x\ne 0$ nên $t\ge 1$ hoặc $t\le -1$)

Ta được phương trình: 3t2 + t – 2 = 0$\iff \left[\begin{array}{l}t=-1\\ t=\frac{2}{3}\left(Loại\right)\end{array}\right.$

Khi đó $\frac{1}{\sin x}=-1$$\iff \sin x=-1$$\iff x=-\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$

Vậy họ nghiệm của phương trình là: $x=-\frac{\pi }{2}+k2\pi ;k\in \mathbb{Z}$.

4. Bài tập tự luyện

Câu 1. Nghiệm của phương trình lượng giác: 2cos2x + 3sinx – 3 = 0 thỏa mãn điều kiện $0<x<\frac{\pi }{2}$ là:

A. $x=\frac{\pi }{2} , x=\frac{\pi }{3}$

B. $x=\frac{\pi }{2} , x=\frac{\pi }{3}$

C. $x=\frac{\pi }{6}$

D. $x=\frac{5\pi }{6}$

Câu 2. Các họ nghiệm của phương trình cos2x – sinx = 0 là:

A. $\frac{\pi }{6}+k2\pi ;-\frac{\pi }{2}+k2\pi ;k\in \mathbb{Z}$

B. $\frac{5\pi }{6}+k2\pi ;-\frac{\pi }{2}+k2\pi ;k\in \mathbb{Z}$

C. $\frac{\pi }{6}+\frac{k2\pi }{3};k\in \mathbb{Z}$

D. $-\frac{\pi }{6}+\frac{k2\pi }{3};k\in \mathbb{Z}$

Câu 3. Nghiệm dương bé nhất của phương trình: 2sin2x + 5sinx – 3 = 0 là:

A. $x=\frac{\pi }{2}$

B. $x=\frac{3\pi }{2}$

C. $x=\frac{5\pi }{6}$

D. $x=\frac{\pi }{6}$

Câu 4. Nghiệm của phương trình $2\cos 2x+2\cos x-\sqrt{2}=0$ là

A. $x=\pm \frac{\pi }{4}+k2\pi ;k\in \mathbb{Z}$

B. $x=\pm \frac{\pi }{4}+k\pi ;k\in \mathbb{Z}$

C. $x=\pm \frac{\pi }{3}+k2\pi ;k\in \mathbb{Z}$

D. $x=\pm \frac{\pi }{3}+k\pi ;k\in \mathbb{Z}$

Câu 5. Trong $\left[0;2\pi \right)$, phương trình sinx = 1 – cos2x có tập nghiệm là:

A. $\left\{\frac{\pi }{2};\pi ;2\pi \right\}$

B. $\left\{0;\pi \right\}$

C. $\left\{0;\frac{\pi }{2};\pi \right\}$

D. $\left\{0;\frac{\pi }{2};\pi ;2\pi \right\}$

Câu 6. Có bao nhiêu nghiệm của phương trình cos4x + 3sin2x + 1 = 0 thuộc khoảng $\left(0;2\pi \right)$?

A. 1

B. 2

C. 3

D. 4

Câu 7. Phương trình ${\sin }^2\frac{x}{3}-2\cos \frac{x}{3}+2=0$ có các nghiệm là:

A. $x=k\pi ,k\in \mathbb{Z}$

B. $x=k3\pi ,k\in \mathbb{Z}$

C. $x=k2\pi ,k\in \mathbb{Z}$

D. $x=k6\pi ,k\in \mathbb{Z}$

Câu 8. Họ nghiệm của phương trình 3cos4x + 2cos2x – 5 = 0 là:

A. $k2\pi ;k\in \mathbb{Z}$

B. $\frac{\pi }{3}+k2\pi ;k\in \mathbb{Z}$

C. $k\pi ;k\in \mathbb{Z}$

D. $-\frac{\pi }{3}+k2\pi ;k\in \mathbb{Z}$

Câu 9. Phương trình tan2x + 5tanx – 6 = 0 có các nghiệm là:

A. $x=\frac{\pi }{4}+k\pi ;x=\arctan (-6)+k\pi ;k\in \mathbb{Z}$

B. $x=\frac{\pi }{4}+k2\pi ;x=\arctan (-6)+k2\pi ;k\in \mathbb{Z}$

C. $x=-\frac{\pi }{4}+k\pi ;x=\arctan (-6)+k2\pi ;k\in \mathbb{Z}$

D. $x=k\pi ;x=\arctan (-6)+k\pi ;k\in \mathbb{Z}$

Câu 10. Một họ nghiệm của phương trình $3\tan 2x+2\cot 2x-5=0$ là

A. $-\frac{\pi }{4}+\frac{k\pi }{2};k\in \mathbb{Z}$

B. $\frac{\pi }{4}+\frac{k\pi }{2};k\in \mathbb{Z}$

C. $-\frac{1}{2}\arctan \frac{2}{3}+\frac{k\pi }{2};k\in \mathbb{Z}$

D. $\frac{1}{2}\arctan \frac{2}{3}+\frac{k\pi }{2};k\in \mathbb{Z}$

Câu 11. Số nghiệm của phương trình 2tanx – 2cotx – 3 = 0 trong khoảng $\left(-\frac{\pi }{2};\pi \right)$ là:

A. 2

B. 1

C. 4

D. 3

Câu 12. Phương trình cos2x + sin2x + 2cosx + 1 = 0 có nghiệm là:

A. $\left[\begin{array}{l}x=k2\pi \\ x=\frac{\pi }{3}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

B. $x=\pm \frac{\pi }{3}+k\pi ;k\in \mathbb{Z}$

C. $x=\frac{\pi }{3}+k2\pi ;k\in \mathbb{Z}$

D. $x=\pi +k2\pi ;k\in \mathbb{Z}$

Câu 13. Các nghiệm của phương trình $\sqrt{3}\tan x+\cot x-\sqrt{3}-1=0$ là:

A. $\left[\begin{array}{l}x=\frac{\pi }{4}+k\pi \\ x=\frac{\pi }{6}+k\frac{\pi }{2}\end{array}\right.\left(k\in \mathbb{Z}\right)$

B. $\left[\begin{array}{l}x=\frac{\pi }{4}+k2\pi \\ x=\frac{\pi }{6}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

C. $\left[\begin{array}{l}x=\frac{\pi }{4}+k3\pi \\ x=\frac{\pi }{6}+k3\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

D. $\left[\begin{array}{l}x=\frac{\pi }{4}+k\pi \\ x=\frac{\pi }{6}+k\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

Câu 14. Số nghiệm của phương trình $\frac{{\sin }^{2}x}{1-\cos x}=1$ thuộc $\left(-\frac{\pi }{2};0\right)$ là:

A. 2

B. 0

C. 1

D. 3

Câu 15. Họ nghiệm của phương trình cos2x + sinx + 1 = 0 là:

A. $x=-\frac{\pi }{2}+k2\pi ;k\in \mathbb{Z}$

B. $x=k\pi ;k\in \mathbb{Z}$

C. $x=\frac{\pi }{2}+k2\pi ;k\in \mathbb{Z}$

D. $x=\frac{\pi }{2}+k\pi ;k\in \mathbb{Z}$

Bảng đáp án