100 công thức về tính thể tích khối cầu chi tiết nhất (2024 có đáp án) và cách giải các dạng toán

Công thức tính thể tích khối cầu chi tiết nhất 

1. Công thức tính thể tích khối cầu

- Khối cầu bán kính r có thể tích là : $V=\frac{4}{3}\pi r^3$

- Chú ý: Thể tích V của khối cầu bán kính r bằng thể tích khối chóp có diện tích đáy bằng diện tích mặt cầu và có chiều cao bằng bán kính của khối cầu đó.

2. Một số ví dụ

VD1. Tính thể tích của khối cầu có bán kính bằng 5

Lời giải:

Thể tích khối cầu đã cho là $V=\frac{4}{3}\pi {.5}^3=\frac{500}{3}\pi$

VD2. Cho mặt cầu có diện tích là $96\pi a^2$. Tính thể tích của khối cầu đó.

Lời giải:

Diện tích mặt cầu là :

$$\begin{gathered} S=4\pi r^2=96\pi a^2 \\ \Rightarrow r=2\sqrt{6}a \end{gathered}$$

Suy ra thể tích khối cầu là: 

$V=\frac{4}{3}\pi .{\left(2\sqrt{6}a\right)}^3=64\sqrt{6}\pi$

VD3. Cho hình chóp S.ABC có 4 đỉnh đều nằm trên một mặt cầu. Biết

$SA=a;SB=2a;SC=a$ và 3 cạnh SA, SB, SC đôi một vuông góc. Tính diện tích mặt cầu và thể tích khối cầu đó.

Lời giải:

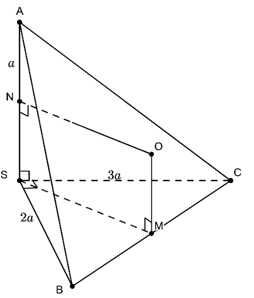
Ta có: 

$\left\{\begin{array}{l}SA\perp SB\\ SA\perp SC\end{array}\right.\Rightarrow SA\perp \left(SBC\right)$

Do SBC là tam giác vuông nên trung điểm M của BC là tâm đường tròn ngoại tiếp

Từ M kẻ đường thẳng $∆$ vuông góc với (SBC) $\Rightarrow ∆$// SA

Kẻ đường trung trực d của SA. d qua trung điểm N của SA và cắt $∆$ tại O

Khi đó O là tâm mặt cầu ngoại tiếp S.ABC.

Tứ giác SNOM có 3 góc vuông nên là hình chữ nhật.

$\Rightarrow r=SO=\sqrt{S{N}^2+S{M}^2}$

Ta có 

$$\begin{gathered} BC=\sqrt{S{B}^2+S{C}^2}=a\sqrt{13} \\ \Rightarrow SM=\frac{a\sqrt{13}}{2} \\ \Rightarrow r=\sqrt{{\left(\frac{a}{2}\right)}^2+{\left(\frac{a\sqrt{13}}{2}\right)}^2}=\frac{a\sqrt{14}}{2} \end{gathered}$$

Diện tích mặt cầu là :

$S=4\pi .{\left(\frac{a\sqrt{14}}{2}\right)}^2=14\pi a^2$

Thể tích mặt cầu là 

$$\begin{gathered} V=\frac{4}{3}\pi .{\left(\frac{a\sqrt{14}}{2}\right)}^3 \\ =\frac{7a^3\sqrt{14}}{3}\pi \end{gathered}$$

VD4. Cho hình chóp tam giác đều S.ABC có đáy cạnh a, mặt bên tạo với đáy góc ${60}^{\circ }$. Tính thể tích khối cầu nội tiếp hình chóp đó.

Lời giải:

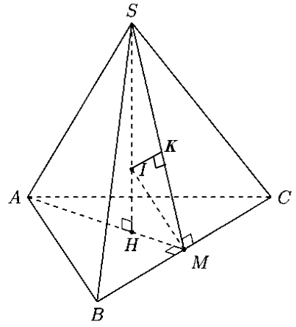
Gọi M là trung điểm BC.

Gọi H là chân đường cao của hình chóp khi đó H là tâm đường tròn ngoại tiếp tam giác đều ABC $\Rightarrow HM=\frac{a\sqrt{3}}{6}$

Gọi I là tâm mặt cầu nội tiếp S.ABC $\Rightarrow I\in SH$

Ta có:

$$\begin{gathered} \left\{\begin{array}{l}\left(SBC\right)\cap \left(ABC\right)=BC\\ AM\perp BC\\ SM\perp BC\end{array}\right. \\ \Rightarrow \left(\left(SBC\right),\left(ABC\right)\right)=\widehat{SMH}={60}^{\circ } \\ \Rightarrow SH=HM.\tan {60}^{\circ }=\frac{a}{2} \end{gathered}$$

Do I là tâm mặt cầu nội tiếp nên:

$$\begin{gathered} r=d\left(I,\left(ABC\right)\right)=d\left(I,\left(SBC\right)\right) \\ \iff IH=IK \end{gathered}$$

$\Rightarrow MI$ là phân giác $\widehat{SMH}$

Theo tính chất phân giác ta có:

$$\begin{gathered} \frac{IS\text{}}{IH}=\frac{SM}{HM}\iff \frac{SH}{IH}=\frac{SM+HM}{HM} \\ SM=\sqrt{S{H}^2+H{M}^2} \\ =\sqrt{\frac{a^2}{4}+\frac{a^2}{12}}=\frac{a\sqrt{3}}{3} \\ \Rightarrow \frac{SM+HM}{HM}=3 \end{gathered}$$

Do đó: $\frac{SH}{IH}=3\Rightarrow r=IH=\frac{a}{6}$

Vậy thể tích khối cầu là $V=\frac{4}{3}\pi .{\left(\frac{a}{6}\right)}^3=\frac{\pi a^3}{162}$