100 bài tập về bất phương trình mũ (2024 có đáp án) và cách giải các dạng toán

Bất phương trình mũ và cách giải các dạng bài tập 

I. LÝ THUYẾT

* Khi giải bất phương trình mũ, ta cần chú ý đến tính đơn điệu của hàm số mũ.

$\boxed{a^{f\left(x\right)}>a^{g\left(x\right)}\iff \left[\begin{array}{l}\left\{\begin{array}{l}a>1\\ f\left(x\right)>g\left(x\right)\end{array}\right.\\ \left\{\begin{array}{l}0<a<1\\ f\left(x\right)<g\left(x\right)\end{array}\right.\end{array}\right.}$

* Tương tự với bất phương trình dạng:

$\left[\begin{array}{l}{a}^{f\left(x\right)}\ge a^{g\left(x\right)}\\ a^{f\left(x\right)}<a^{g\left(x\right)}\\ a^{f\left(x\right)}\le a^{g\left(x\right)}\end{array}\right.$

* Trong trường hợp cơ sốcó chứa ẩn số thì:

$\boxed{a^M>a^N\iff \left(a-1\right)\left(M-N\right)>0}$

* Ta cũng thường sử dụng các phương pháp giải tương tự như đối với phương trình mũ:

+ Đưa về cùng cơ số.

+ Đặt ẩn phụ.

+ Sử dụng tính đơn điệu:

Hàm số y = f(x) nghịch biến trên D thì:

$f\left(u\right)<f\left(v\right)\Rightarrow u>v$

Hàm số y = f(x) đồng biến biến trên D thì:

$f\left(u\right)<f\left(v\right)\Rightarrow u<v$

II. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI

Dạng 1. Bất phương trình mũ cơ bản

A. Phương pháp

Xét bất phương trình có dạng: $a^x>b.$

- Nếu $b\le 0$, tập nghiệm của bất phương trình là R, vì $a^x>b,\forall x\in ℝ.$.

- Nếu $b>0$ thì bất phương trình tương đương với $a^x>a^{{\log }_{a}b}.$

+Với $a>1$, nghiệm của bất phương trình là $x>{\log }_{a}b.$

+Với $0<a<1$, nghiệm của bất phương trình là $x<{\log }_{a}b.$

Chú ý

+ Xét bất phương trình: $a^{f\left(x\right)}>b\left(1\right)$

Nếu $\left\{\begin{array}{c}0<a\ne 1\\ b\le 0\end{array}\right.$ thì (1) luôn đúng.

Nếu $\left\{\begin{array}{c}b>0\\ 0<a<1\end{array}\right.$thì $\left(1\right)\iff f\left(x\right)<{\log }_{a}b$

Nếu $\left\{\begin{array}{c}b>0\\ 1<a\end{array}\right.$thì $\left(1\right)\iff f\left(x\right)>{\log }_{a}b$

+ Xét bất phương trình: $a^{f\left(x\right)}<b\left(2\right)$

Nếu $\left\{\begin{array}{c}0<a\ne 1\\ b\le 0\end{array}\right.$ thì (2) vô nghiệm.

Nếu $\left\{\begin{array}{c}b>0\\ 0<a<1\end{array}\right.$ thì $\left(2\right)\iff f\left(x\right)>{\log }_{a}b$

Nếu $\left\{\begin{array}{c}b>0\\ 1<a\end{array}\right.$ thì $\left(2\right)\iff f\left(x\right)<{\log }_{a}b$ : °aABC

B. Ví dụ minh họa

Câu 1: Tập nghiệm của bất phương trình $2^x>3^{x+1}$ là

A. $\left(-\infty ;{\log }_{2}3\right]$

B. $\left(-\infty ;{\log }_{\frac{2}{3}}3\right)$

C. $\varnothing$

D. $\left({\log }_{\frac{2}{3}}3;+\infty \right)$

Hướng dẫn giải

Chọn B.

Ta có:

$$\begin{gathered} 2^x>3^{x+1}\iff 2^x>{3.3}^x \\ \iff {\left(\frac{2}{3}\right)}^x>3\iff x<{\log }_{\frac{2}{3}}3 \end{gathered}$$

Vậy tập nghiệm của BPT là $S=\left(-\infty ;{\log }_{\frac{2}{3}}3\right)$.

Câu 2: Tập nghiệm của bất phương trình $2^x+2^{x+1}\le 3^x+3^{x-1}$

A. $x\in \left[2;+\infty \right)$

B. $x\in \left(2;+\infty \right)$

C. $x\in \left(-\infty ;2\right)$

D. $\left(2;+\infty \right)$

Hướng dẫn giải

$$\begin{gathered} 2^x+2^{x+1}\le 3^x+3^{x-1} \\ \iff {3.2}^x\le \frac{4}{3}{.3}^x \\ \iff {\left(\frac{3}{2}\right)}^x\ge \frac{9}{4} \\ \iff x\ge 2 \end{gathered}$$

Vậy tập nghiệm của BPT là $S=\left[2;+\infty \right)$

Chọn D.

Câu 3: Nghiệm của bất phương trình $\frac{3^x}{3^x-2}<3$ là:

A. $\left[\begin{array}{l}x>1\\ x<{\log }_{3}2\end{array}\right.$

B. $x>{\log }_{3}2$

C. $x<1$

D. ${\log }_{3}2<x<1$

Hướng dẫn giải

$$\begin{gathered} \frac{3^x}{3^x-2}<3\iff \frac{3^x-3}{3^x-2}>0 \\ \iff \left[\begin{array}{l}{3}^x>3\\ 3^x<2\end{array}\right.\iff \left[\begin{array}{l}x>1\\ x<{\log }_{3}2\end{array}\right. \end{gathered}$$

Chọn A.

Câu 4: Tập nghiệm của bất phương trình: ${81.9}^{x-2}+3^{x+\sqrt{x}}-\frac{2}{3}{.3}^{2\sqrt{x}+1}\ge 0$ là:

A. $S=\left[1;+\infty \right)\cup \left\{0\right\}$

B. $S=\left[1;+\infty \right)$

C. $S=\left[0;+\infty \right)$

D. $S=\left[2;+\infty \right)\cup \left\{0\right\}$

Hướng dẫn giải

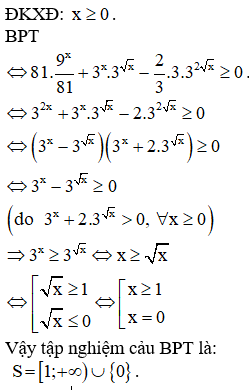
Chọn A.

Câu 5: Tập nghiệm của bất phương trình $2^x+{4.5}^x-4<{10}^x$ là:

A. $\left[\begin{array}{l}x<0\\ x>2\end{array}\right..$

B. $x<0.$

C. $x>2.$

D. $0<x<2.$

Hướng dẫn giải

Chọn A.

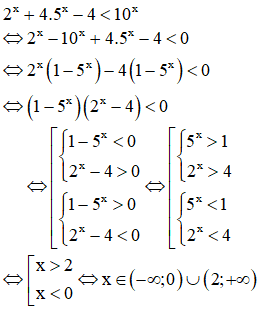
Dạng 2. Phương pháp đưa về cùng cơ số

A. Phương pháp

Xét bất phương trình $a^{f\left(x\right)}>a^{g\left(x\right)}$

Nếu a > 1 thì $a^{f\left(x\right)}>a^{g\left(x\right)}\iff f\left(x\right)>g\left(x\right)$ (cùng chiều khi a > 1)

Nếu 0 < a < 1 thì $a^{f\left(x\right)}>a^{g\left(x\right)}\iff f\left(x\right)<g\left(x\right)$ (ngược chiều khi 0 < a < 1)

Nếu a chứa ẩn thì $a^{f\left(x\right)}>a^{g\left(x\right)}\iff (a-1)\left[f\left(x\right)-g\left(x\right)\right]>0$(hoặc xét 2 trường hợp của cơ số).

B. Ví dụ minh họa

Câu 1: Tìm tập nghiệm của bất phương trình $2^{x-1}>{\left(\frac{1}{16}\right)}^{\frac{1}{x}}$.

A. $S=\left(2;+\infty \right)$

B. $S=\left(-\infty ;0\right)$

C. $S=\left(0;+\infty \right)$

D. $S=\left(-\infty ;+\infty \right)$

Hướng dẫn giải

Chọn C.

Câu 2: Tìm số nghiệm nguyên dương của bất phương trình ${\left(\frac{1}{5}\right)}^{x^2-2x}\ge \frac{1}{125}$.

A. 3

B. 4

C. 5

D. 6

Hướng dẫn giải

Chọn A.

Ta có

$$\begin{gathered} {\left(\frac{1}{5}\right)}^{x^2-2x}\ge \frac{1}{125} \\ \iff x^2-2x\le 3 \\ \iff \left(x+1\right)\left(x-3\right)\le 0 \\ \iff -1\le x\le 3 \end{gathered}$$

Vì phương trình tìm nghiệm nguyên dương nên các nghiệm là $x=\left\{1;2;3\right\}$.

Vậy có tất cả ba nghiệm nguyên dương của BPT.

Câu 3: Giải bất phương trình ${\left(\frac{1}{3}\right)}^{-3x^2}<3^{2x+1}$ ta được tập nghiệm:

A. $\left(-\infty ;-\frac{1}{3}\right)$

B. $\left(1;+\infty \right)$

C. $\left(-\frac{1}{3};1\right)$

D. $\left(-\infty ;-\frac{1}{3}\right)\cup \left(1;+\infty \right)$

Hướng dẫn giải

Chọn C.

Ta có

$$\begin{gathered} {\left(\frac{1}{3}\right)}^{-3x^2}<3^{2x+1} \\ \iff 3x^2<2x+1 \\ \iff -\frac{1}{3}<x<1 \end{gathered}$$

Vậy tập nghiệm của BPT là $S=\left(-\frac{1}{3};1\right)$.

Câu 4: Tập nghiệm của bất phương trình $2^{x+2}<{\left(\frac{1}{4}\right)}^x$ là

A. $\left(-\infty ;-\frac{2}{3}\right)$

B. $\left(0;+\infty \right)\backslash \left\{1\right\}$

C. $\left(-\infty ;0\right)$

D. $\left(-\frac{2}{3};+\infty \right)$

Hướng dẫn giải

Chọn A.

Ta có :

$$\begin{gathered} 2^{x+2}<{\left(\frac{1}{4}\right)}^x\iff 2^{x+2}<2 \\ \iff x+2<-2x\iff x<-\frac{2}{3} \end{gathered}$$

Vậy tập nghiệm của bất phương trình là $S=\left(-\infty ;-\frac{2}{3}\right)$.

Câu 5: Tìm tập nghiệm S của bất phương trình ${\left(\frac{1}{2}\right)}^{2x+1}<{\left(\frac{1}{2}\right)}^{3x-2}$

A. $S=\left(-\infty ;3\right)$

B. $S=\left(3;+\infty \right)$

C. $S=\left(-\infty ;-3\right)$

D. $S=\left(-\frac{1}{2};3\right)$

Hướng dẫn giải

Chọn A

Ta có:

$$\begin{gathered} {\left(\frac{1}{2}\right)}^{2x+1}<{\left(\frac{1}{2}\right)}^{3x-2} \\ \iff 2x+1>3x-2 \end{gathered}$$

(vì $0<\frac{1}{2}<1$) $\iff x<3$

Vậy tập nghiệm của BPT có dạng $S=\left(-\infty ;3\right)$.

Dạng 3. Phương pháp đặt ẩn phụ

A. Phương pháp giải:

Ta sẽ làm tương tự như các dạng đặt ẩn phụ của phương trình nhưng lưu ý đến chiều biến thiên của hàm số.

B. Ví dụ minh họa

Câu 1: Tập nghiệm của bất phương trình: $3^{2x+1}-{10.3}^x+3\le 0$ là

A. $\left[-1;0\right)$

B. $\left(-1;1\right)$

C. $\left(0;1\right]$.

D. $\left[-1;1\right]$

Hướng dẫn giải

Chọn D.

Câu 2: Nghiệm của bất phương trình $e^x+e^{-x}<\frac{5}{2}$ là

A. $x<\frac{1}{2}$ hoặc $x>2$.

B. $\frac{1}{2}<x<2$.

C. $-\ln 2<x<\ln 2$

D. $x<-\ln 2$ hoặc $x>\ln 2$.

Hướng dẫn giải

Chọn C.

Ta có :

$$\begin{gathered} e^x+e^{-x}<\frac{5}{2}\iff e^x+\frac{1}{e^x}<\frac{5}{2} \\ \iff 2{\left(e^x\right)}^2-5e^x+2<0 \\ \iff \frac{1}{2}<e^x<2 \\ \iff -\ln 2<x<\ln 2 \end{gathered}$$

Câu 3: Nghiệm của bất phương trình $9^{x-1}-{36.3}^{x-3}+3\le 0$ là

A. $x\ge 1$

B. $x\le 3$

C. $1\le x\le 3$

D. $1\le x\le 2$

Hướng dẫn giải

Chọn D.

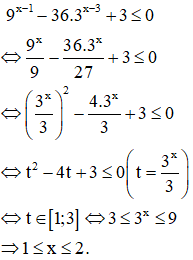
Câu 4: Bất phương trình $9^x-3^x-6<0$ có tập nghiệm là

A. $\left(-\infty ;1\right)$

B. $\left(-\infty ;-2\right)\cup \left(3;+\infty \right)$

C. $\left(1;+\infty \right)$

D. $\left(-2;3\right)$.

Hướng dẫn giải

Chọn A.

$$\begin{gathered} 9^x-3^x-6<0 \\ \iff {\left(3^x\right)}^2-3^x-6<0 \\ \iff -2<3^x<3\iff x<1 \end{gathered}$$

Vậy tập nghiệm của BPT là $S=\left(-\infty ;1\right)$.

Câu 5: Tập hợp nghiệm của bất phương trình $3^{3x-2}+\frac{1}{{27}^x}\le \frac{2}{3}$ là

A. $\left(0;1\right).$

B. $\left(1;2\right).$

C. $\left\{\frac{1}{3}\right\}.$

D. $\left(2;3\right).$

Hướng dẫn giải

Chọn C.

Ta có

$$\begin{gathered} 3^{3x-2}+\frac{1}{{27}^x}\le \frac{2}{3} \\ \iff \frac{3^{3x}}{9}+\frac{1}{3^{3x}}\le \frac{2}{3} \\ \iff {\left(3^{3x}\right)}^2-{6.3}^{3x}+9\le 0 \\ \iff {\left(3^{3x}-3\right)}^2\le 0 \\ \iff 3^{3x}-3=0\iff x=\frac{1}{3}. \end{gathered}$$

Vậy tập nghiệm của BPT là $S=\left\{\frac{1}{3}\right\}.$

Câu 6: Nghiệm của bất phương trình $\frac{1}{3^x+5}\le \frac{1}{3^{x+1}-1}$ là:

A. $-1<x\le 1.$

B. $x\le -1.$

C. $x>1.$

D. $1<x<2.$

Hướng dẫn giải

Đặt $t=3^x$ ($t>0$), khi đó bất phương trình đã cho tương đương với

$$\begin{gathered} \frac{1}{t+5}\le \frac{1}{3t-1} \\ \iff \left\{\begin{array}{l}3t-1>0\\ 3t-1\le t+5\end{array}\right. \\ \iff \frac{1}{3}<t\le 3\iff -1<x\le 1. \end{gathered}$$

Chọn A.

Dạng 4. Phương pháp logarit hóa

A. Phương pháp

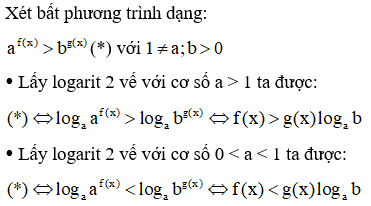
B. Ví dụ minh họa

Câu 1: Tìm tập của bất phương trình: $3^x{.5}^{x^2}<1$

A. $\left(-{\log }_{5}3;0\right]$

B. $\left[{\log }_{3}5;0\right)$

C. $\left(-{\log }_{5}3;0\right)$

D. $\left({\log }_{3}5;0\right)$

Hướng dẫn giải:

Chọn C.

Ta có:

$$\begin{gathered} 3^x{.5}^{x^2}<1\iff {\log }_5\left(3^x{.5}^{x^2}\right)<0 \\ \iff x^2+x{\log }_{5}3<0 \\ \iff -{\log }_{5}3<x<0 \end{gathered}$$

nên $S=\left(-{\log }_{5}3;0\right)$

Câu 2: Cho hàm số $f\left(x\right)=2^x{.3}^{x^2}$. Khẳng định nào sau đây là sai?

A. $f\left(x\right)<1\iff x{\log }_{\frac{1}{3}}2-x^2>0$

B. $f\left(x\right)<1\iff x+x^2{\log }_{2}3>0$

C. $f\left(x\right)<1\iff x{\log }_{3}2+x^2<0$

D. $f\left(x\right)<1\iff x\ln 2+x^2\ln 3<0$

Hướng dẫn giải:

Chọn B.

Ta có

$$\begin{gathered} f\left(x\right)<1\iff \left[\begin{array}{l}{\log }_{\frac{1}{3}}\left(2^x{.3}^{x^2}\right)<{\log }_{\frac{1}{3}}1\\ {\log }_2\left(2^x{.3}^{x^2}\right)<{\log }_{2}1\\ {\log }_3\left(2^x{.3}^{x^2}\right)<{\log }_{3}1\\ \ln \left(2^x{.3}^{x^2}\right)<\ln 1\end{array}\right. \\ \iff \left[\begin{array}{l}x{\log }_{\frac{1}{3}}2-x^2>0\\ x+x^2{\log }_{2}3<0\\ x{\log }_{3}2+x^2<0\\ x\ln 2+x^2\ln 3<0\end{array}\right. \end{gathered}$$

Đáp án sai là B.

III. BÀI TẬP TỰ LUYỆN

Câu 1: Tập nghiệm của bất phương trình $\frac{{2.3}^x-2^{x+2}}{3^x-2^x}\le 1$ là:

A. $x\in \left(0;{\log }_{\frac{3}{2}}3\right].$

B. $x\in \left(1;3\right).$

C. $x\in \left(1;3\right].$

D. $x\in \left[0;{\log }_{\frac{3}{2}}3\right].$

Câu 2: Tập nghiệm của bất phương trình $4^x+4^{x+2}+4^{x+4}\ge 5^x+5^{x+2}+5^{x+4}$ là:

A. $T=\left(-\infty ;{\log }_{\frac{4}{5}}\frac{31}{13}\right].$

B. $T=\left[{\log }_{\frac{4}{5}}\frac{31}{13};+\infty \right).$

C. $T=\left(-\infty ;{\log }_{\frac{4}{5}}\frac{31}{13}\right).$

D. $T=\left({\log }_{\frac{4}{5}}\frac{31}{13};+\infty \right).$

Câu 3: Cho bất phương trình: $3^x+3^{x+1}+3^{x+2}\le 4^x+4^{x+1}+4^{x+2}\left(1\right)$

Tập nghiệm của bất phương trình (1) là:

A. $\left[{\log }_{\frac{3}{4}}\frac{21}{13};+\infty \right)$

B. $\left(-\infty ;{\log }_{\frac{3}{4}}\frac{21}{13}\right]$

C. $\left({\log }_{\frac{3}{4}}\frac{21}{13};+\infty \right)$

D. $\left(-\infty ;{\log }_{\frac{3}{4}}\frac{21}{13}\right)$.

Câu 4: Tập nghiệm của bất phương trình $3^x.x^2+54x+{5.3}^x>9x^2+6x{.3}^x+45$ là:

A. $\left(-\infty ;1\right)\cup \left(2;+\infty \right)$.

B. $\left(-\infty ;1\right)\cup \left(2;5\right)$.

C. $\left(-\infty ;1\right)\cup \left(5;+\infty \right)$.

D. $\left(1;2\right)\cup \left(5;+\infty \right)$.

Câu 5: Tập nghiệm của bất phương trình $\left(2^x-4\right)\left(x^2-2x-3\right)<0$ là

A. $\left(-\infty ;-1\right)\cup \left(2;3\right)$

B. $\left(-\infty ;1\right)\cup \left(2;3\right)$

C. $\left(2;3\right)$

D. $\left(-\infty ;-2\right)\cup \left(2;3\right)$

Câu 6: Nghiệm của bất phương trình $3^{x+2}\ge \frac{1}{9}$ là:

A. $x\ge -4$

B. $x<0$

C. $x>0$

D. $x<4$.

Câu 7: Tìm tất cả các nghiệm của bất phương trình: $2^{-\left|x\right|}>\frac{1}{8}$

A. x > 3 hoặc x < -3.

B. -3

C. x < -3

D. x >3

Câu 8: Giải bất phương trình $2^{-x^2+3x}>4$

A. $\left[{}_{x<1}^{x>2}\right.$

B. $2<x<4$

C. $1<x<2.$

D. $0<x<2.$

Câu 9: Tìm tập nghiệm của bất phương trình $0,3^{x^2+x}>0,09$

A. $\left(-\infty ;-2\right)$

B. $\left(-\infty ;-2\right)\cup \left(1;+\infty \right)$

C. $\left(-2;1\right)$

D. $\left(1;+\infty \right)$.

Câu 10: Tìm tập nghiệm S của bất phương trình ${\left(\frac{\pi }{3}\right)}^{\frac{1}{x}}<{\left(\frac{\pi }{3}\right)}^{\frac{3}{x}+5}$

A. $S=\left(-\infty ;\frac{-2}{5}\right)$

B. $S=\left(-\infty ;\frac{-2}{5}\right)\cup \left(0;+\infty \right).$

C. $S=\left(0;+\infty \right).$

D. $S=\left(\frac{-2}{5};+\infty \right).$

Câu 11: Tập các số x thỏa mãn ${\left(\frac{3}{2}\right)}^{4x}\le {\left(\frac{3}{2}\right)}^{2-x}$ là:

A. $\left(-\infty ;\frac{2}{3}\right]$

B. $\left[-\frac{2}{3};+\infty \right)$

C. $\left(-\infty ;\frac{2}{5}\right]$

D. $\left[\frac{2}{5};+\infty \right)$

Câu 12: Tập nghiệm của bất phương trình ${\left(\sqrt{5}-2\right)}^{\frac{2x}{x-1}}\le {\left(\sqrt{5}+2\right)}^x$ là:

A. $\left(-\infty ;-1\right]\cup \left[0;1\right]$

B. $\left[-1;0\right]$

C. $\left(-\infty ;-1\right)\cup \left[0;+\infty \right)$

D. $\left[-1;0\right]\cup \left(1;+\infty \right)$.

Câu 13: Nghiệm của bất phương trình ${\left(\frac{1}{2}\right)}^{9x^2-17x+11}\ge {\left(\frac{1}{2}\right)}^{7-5x}$ là

A. $x\le \frac{2}{3}$

B. $x>\frac{2}{3}$

C. $x\ne \frac{2}{3}$

D. $x=\frac{2}{3}$

Câu 14: Tập nghiệm của bất phương trình $\frac{1}{2^{\sqrt{x^2-2x}}}-\frac{2^x}{2}\le 0$ là

A. $\left[0;2\right]$

B. $\left(-\infty ;1\right]$

C. $\left(-\infty ;0\right]$

D. $\left[2;+\infty \right)$.

Câu 15: Bất phương trình ${2.5}^{x+2}+{5.2}^{x+2}\le 133.\sqrt{{10}^x}$ có tập nghiệm là $S=\left[a;b\right]$ thì bằng

A. 6.

B. 10.

C. 12.

D. 16.

Câu 16: Bất phương trình ${2.5}^{x+2}+{5.2}^{x+2}\le 133.\sqrt{{10}^x}$ có tập nghiệm là $S=\left[a;b\right]$ thì $b-2a$ bằng

A. 6.

B. 10.

C. 12.

D. 16.

Câu 17: Giải bất phương trình $2^{\frac{4x-1}{2x+1}}<2^{\frac{2-2x}{2x+1}}+1.$

A. $\left[\begin{array}{c}x<-\frac{1}{2}\\ x>1\end{array}\right.$

B. $-\frac{1}{2}<x<1$

C. $x>1$

D. $x<-\frac{1}{2}$.

Câu 18: Tìm m để bất phương trình $m{.9}^x-(2m+1){.6}^x+m{.4}^x\le 0$ nghiệm đúng với mọi $x\in \left(0;1\right)$.

A. $0\le m\le 6$

B. $m\le 6$

C. $m\ge 6$

D. $m\le 0$

ĐÁP ÁN