100 bài tập về định lý Ta-lét trong không gian (2024 có đáp án) và cách giải các dạng toán

Định lý Ta-lét trong không gian 

1. Lý thuyết

+ Định lý Ta – let

Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.

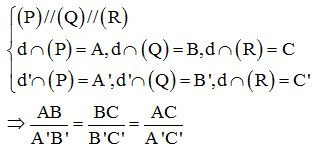
+ Định lý Ta-lét đảo:

Cho hai đường thẳng d và d’ chéo nhau và các điểm A, B, C trên d, các điểm A’, B’, C’ trên d’ sao cho $\frac{AB}{A\text{'}B\text{'}}=\frac{BC}{B\text{'}C\text{'}}=\frac{AC}{A\text{'}C\text{'}}$. Khi đó các đường thẳng AA’, BB’, CC’ cùng song song với một mặt phẳng.

2. Công thức giải

Áp dụng định lý Ta–lét (thuận và đảo) để chứng minh tỉ lệ đoạn thẳng và chứng minh tồn tại mặt phẳng song song với các đường thẳng.

3. Ví dụ minh họa

Ví dụ 1: Cho hình chóp S.ABC có đáy là tam giác ABC thỏa mãn AB = AC = 4, $\widehat{BAC}=30°.$ Mặt phẳng (P) song song với (ABC) cắt đoạn SA tại M sao cho SM = 2MA. Diện tích thiết diện của (P) và hình chóp S.ABC bằng bao nhiêu?

Lời giải

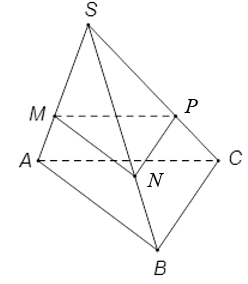
Diện tích tam giác ABC là

$S_{\Delta ABC}=\frac{1}{2}.AB.AC.\sin \widehat{BAC}$$=\frac{1}{2}\mathrm{.4.4.}\sin {30}^0=4.$

Gọi N, P lần lượt là giao điểm của mặt phẳng (P) và các cạnh SB, SC.

Vì (P) // (ABC) nên theo định lý Talet, ta có $\frac{SM}{SA}=\frac{SN}{SB}=\frac{SP}{SC}=\frac{2}{3}.$

Khi đó (P) cắt hình chóp S.ABC theo thiết diện là tam giác MNP đồng dạng với tam giác ABC theo tỉ số $k=\frac{2}{3}.$

Do đó $\frac{S_{\Delta MNP}}{S_{\Delta ABC}}=k^2={\left(\frac{2}{3}\right)}^2$

Vậy $S_{\Delta MNP}={\left(\frac{2}{3}\right)}^2.S_{\Delta ABC}={\left(\frac{2}{3}\right)}^2.4=\frac{16}{9}.$

Ví dụ 2: Cho tứ diện ABCD. Gọi I, J là hai điểm di động lần lượt trên các cạnh AD, BC sao cho $\frac{IA}{ID}=\frac{JB}{JC}$. Chứng minh rằng: IJ luôn song song với một mặt phẳng cố định.

Lời giải

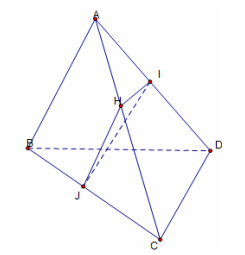
Trong (ACD): dựng IH // CD với $H\in AC$

Xét tam giác ACD có HI // CD nên $\frac{IA}{ID}=\frac{HA}{HC}$

Mà $\frac{IA}{ID}=\frac{JB}{JC}$, do đó $\frac{IA}{ID}=\frac{HA}{HC}=\frac{JB}{JC}$

Xét tam giác ABC có $\frac{HA}{HC}=\frac{JB}{JC}$ nên HJ // AB.

Dựng mặt phẳng (P) đi qua CD và song song với AB. Ta có mặt phẳng (P) cố định.

Ta có: $\left\{\begin{array}{l}CD//HI\\ CD\subset \left(P\right)\end{array}\right.$$\Rightarrow HI//\left(P\right)$ và có $\left\{\begin{array}{l}HJ//AB\\ AB//\left(P\right)\end{array}\right.$$\Rightarrow HJ//\left(P\right)$

Do đó $\left\{\begin{array}{l}HI,HJ\subset \left(HIJ\right)\\ HI\cap HJ=H\\ HI//\left(P\right)\\ HJ//\left(P\right)\end{array}\right.$$\Rightarrow \left(HIJ\right)//\left(P\right)$ mà $IJ\subset \left(HIJ\right)$$\Rightarrow IJ//\left(P\right)$

Vậy IJ song song với mặt phẳng cố định.

4. Bài tập tự luyện

Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I là trung điểm của SA và J, K là các điểm trên SB, SC sao cho JS = 2JB, KS = 2KC. Đường thẳng SD cắt mặt phẳng (IJK) tại M; E là giao điểm của hai đường thẳng IJ và KM. Tỉ số $T=\frac{EI}{EJ}$ bằng

A. $T=\frac{1}{2}.$

B. $T=\frac{2}{3}.$

C. $T=\frac{4}{5}.$

D. $T=\frac{3}{4}.$

Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trên các cạnh SA, SB, SC lần lượt lấy các điểm A’, B’, C’, đường thẳng SD cắt mặt phẳng (A’B’C’) tại D’. Gọi O là giao điểm của AC và BD, đường thẳng A’C’ cắt SO tại I. Mệnh đề nào dưới đây đúng?

A. $\frac{SA}{SA\text{'}}+\frac{SC}{SC\text{'}}=\frac{SO}{SI}.$

B. $\frac{3SA}{2SA\text{'}}+\frac{3SC}{2SC\text{'}}=\frac{SO}{SI}.$

C. $\frac{SA}{SA\text{'}}+\frac{SC}{SC\text{'}}=\frac{SB}{SB\text{'}}+\frac{SD}{SD\text{'}}.$

D. $\frac{SA}{SA\text{'}}+\frac{SC}{SC\text{'}}+\frac{SB}{SB\text{'}}+\frac{SD}{SD\text{'}}=3\frac{SO}{SI}.$

Đáp án: 1A, 2C