100 bài tập về phương pháp xét tính đồng biến, nghịch biến của hàm số (2024 có đáp án) và cách giải các dạng toán

Phương pháp xét tính đồng biến, nghịch biến của hàm số chi tiết nhất

I. Lí thuyết tổng hợp

- Cho K là một khoảng hoặc một đoạn hoặc nửa khoảng, y = f(x) là hàm số xác định trên K.

+ Hàm số y = f(x) đồng biến (tăng) trên K nếu với mọi x thuộc K thì khi x tăng f(x) cùng tăng, khi x giảm f(x) cùng giảm.

+ Hàm số y = f(x) nghịch biến (giảm) trên K nếu với mọi x thuộc K thì khi x tăng f(x) giảm, khi x giảm f(x) tăng.

- Lưu ý.

+ Nếu một hàm số đồng biến trên K thì trên đó, đồ thị của nó đi lên.

+ Nếu một hàm số nghịch biến trên K thì trên đó, đồ thị của nó đi xuống.

+ Hàm số bậc nhất y = ax + b luôn đồng biến hoặc nghịch biến trên .

II. Các công thức

- Cho hàm số y = f(x) xác định trên K. Lấy x1,x2∈K𝑥1,𝑥2∈𝐾 và x1<x2𝑥1<𝑥2.

Đặt T = f(x2)−f(x1)𝑓(𝑥2)−𝑓(𝑥1). Ta có:

T > 0 ⇔⇔ Hàm số y = f(x) đồng biến (tăng) trên K

T < 0 ⇔⇔ Hàm số y = f(x) nghịch biến (giảm) trên K

- Cho hàm số y = f(x) xác định trên K. Lấy x1,x2∈K𝑥1,𝑥2∈𝐾 và x1≠x2𝑥1≠𝑥2.

Đặt T=f(x1)−f(x2)x1−x2𝑇=𝑓(𝑥1)−𝑓(𝑥2)𝑥1−𝑥2. Ta có:

T > 0 ⇔⇔ Hàm số y = f(x) đồng biến (tăng) trên K

T < 0 ⇔⇔ Hàm số y = f(x) nghịch biến (giảm) trên K

- Nếu một hàm số đồng biến trên K thì trên đó, đồ thị của nó đi lên.

- Nếu một hàm số nghịch biến trên K thì trên đó, đồ thị của nó đi xuống.

III. Ví dụ minh họa

Bài 1: Cho hàm số y = f(x) có đồ thị như hình vẽ dưới đây. Xét tính đồng biến, nghịch biến của hàm số trên khoảng (2; 4) và đoạn [-4; -2].

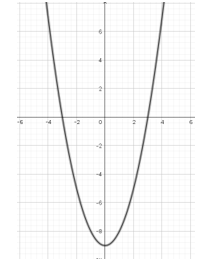
Lời giải:

Ta thấy khi thì đồ thị của hàm số y = f(x) đi lên

⇒⇒ Hàm số y = f(x) đồng biến trên khoảng (2; 4)

Ta thấy khi thì đồ thị của hàm số y = f(x) đi xuống

⇒⇒ Hàm số y = f(x) nghịch biến trên đoạn [-4; -2]

Bài 2: Xét tính đồng biến, nghịch biến của hàm số y=f(x)=x+1−2x−3𝑦=𝑓(𝑥)=𝑥+1−2𝑥−3 trên khoảng (3;+∞)3;+∞.

Lời giải:

- Điều kiện xác định của hàm số y=f(x)=x+1−2x−3𝑦=𝑓(𝑥)=𝑥+1−2𝑥−3 là:x−3≠0⇔x≠3𝑥−3≠0⇔𝑥≠3

Tập xác định của hàm số y = f(x) là: D=R\{3}𝐷=𝑅\{3}

Hàm số y=f(x)=x+1−2x−3𝑦=𝑓(𝑥)=𝑥+1−2𝑥−3 xác định trên khoảng (3;+∞)3;+∞

- Lấy x1,x2∈(3;+∞)𝑥1,𝑥2∈(3;+∞) và x1≠x2𝑥1≠𝑥2. Đặt T=f(x1)−f(x2)x1−x2𝑇=𝑓(𝑥1)−𝑓(𝑥2)𝑥1−𝑥2

⇒T=f(x1)−f(x2)x1−x2=x1+1−2x1−3−(x2+1−2x2−3)x1−x2=x1+1−2x1−3−x2−1+2x2−3x1−x2=x1−x2−2(1x1−3−1x2−3)x1−x2=x1−x2−2[x2−3−x1+3(x1−3)(x2−3)]x1−x2=x1−x2−2[x2−x1(x1−3)(x2−3)]x1−x2=x1−x2+2[x1−x2(x1−3)(x2−3)]x1−x2=1+2(x1−3)(x2−3)1=1+2(x1−3)(x2−3)⇒𝑇=𝑓(𝑥1)−𝑓(𝑥2)𝑥1−𝑥2=𝑥1+1−2𝑥1−3−𝑥2+1−2𝑥2−3𝑥1−𝑥2=𝑥1+1−2𝑥1−3−𝑥2−1+2𝑥2−3𝑥1−𝑥2=𝑥1−𝑥2−21𝑥1−3−1𝑥2−3𝑥1−𝑥2=𝑥1−𝑥2−2𝑥2−3−𝑥1+3(𝑥1−3)(𝑥2−3)𝑥1−𝑥2=𝑥1−𝑥2−2𝑥2−𝑥1(𝑥1−3)(𝑥2−3)𝑥1−𝑥2=𝑥1−𝑥2+2𝑥1−𝑥2(𝑥1−3)(𝑥2−3)𝑥1−𝑥2=1+2(𝑥1−3)(𝑥2−3)1=1+2(𝑥1−3)(𝑥2−3)

Ta thấy trong khoảng (3;+∞)3;+∞ thì T luôn xác định.

Với x1,x2∈(3;+∞)𝑥1,𝑥2∈(3;+∞)

⇒{x1−3>0x2−3>0⇒T=1+2(x1−3)(x2−3)>0⇒𝑥1−3>0𝑥2−3>0⇒𝑇=1+2(𝑥1−3)(𝑥2−3)>0

Hàm số y=f(x)=x+1−2x−3𝑦=𝑓(𝑥)=𝑥+1−2𝑥−3 đồng biến trên khoảng (3;+∞)3;+∞.

Bài 3: Xét tính đồng biến, nghịch biến của hàm số: y=f(x)=x2−4𝑦=𝑓(𝑥)=𝑥2−4 trên khoảng (−∞;0)(−∞;0).

Lời giải:

Hàm số y=f(x)=x2−4𝑦=𝑓(𝑥)=𝑥2−4 xác định trên R

⇒⇒ Hàm số y=f(x)=x2−4𝑦=𝑓(𝑥)=𝑥2−4 xác định trên khoảng (−∞;0)(−∞;0)

Lấy x1,x2∈(−∞;0)𝑥1,𝑥2∈(−∞;0) và x1<x2𝑥1<𝑥2

⇒{x2−x1>0x1+x2<0⇒𝑥2−𝑥1>0𝑥1+𝑥2<0 (1)

Ta có: T=f(x2)−f(x1)𝑇=𝑓(𝑥2)−𝑓(𝑥1)

=(x22−4)−(x12−4)=x22−x12=(x2−x1)(x1+x2)=(𝑥22−4)−(𝑥12−4)=𝑥22−𝑥12=(𝑥2−𝑥1)(𝑥1+𝑥2)(2)

Từ (1) và (2) ⇒T<0⇒𝑇<0⇒⇒ Hàm số y=f(x)=x2−4𝑦=𝑓(𝑥)=𝑥2−4 nghịch biến trên khoảng (−∞;0)(−∞;0)

IV. Bài tập tự luyện

Bài 1: Xét tính đồng biến, nghịch biến của hàm số y = f(x) = 4x – 9 trên toàn tập xác định của nó.

Bài 2: Xét tính đồng biến, nghịch biến của hàm số y=f(x)=x2−5x+7𝑦=𝑓(𝑥)=𝑥2−5𝑥+7 trên các khoảng (−∞;0)(−∞;0) và (4;+∞)(4;+∞).