100 công thức tính GTNN - GTLN của đồ thị hàm số chi tiết nhất (2024 )

Công thức tính GTNN - GTLN của hàm số chi tiết nhất 

1. Lí thuyết

Định nghĩa: Cho hàm số $y=f\left(x\right)$ xác định trên tập D

a. Số M được gọi là giá trị lớn nhất của hàm số $y=f\left(x\right)$ trên D nếu $f\left(x\right)\le M\forall x\in D$ và tồn tại $x_0\in D:f\left(x_0\right)=M$

- Kí hiệu là: $M=\underset{D}{\max }f\left(x\right)$

b. Số m được gọi là giá trị nhỏ nhất của hàm số $y=f\left(x\right)$ trên D nếu $f\left(x\right)\ge M\forall x\in D$ và tồn tại $x_0\in D:f\left(x_0\right)=m$

- Kí hiệu là: $m=\underset{D}{\min }f\left(x\right)$

2. Các bước tìm GTLN - GTNN của hàm số trên D hoặc trên một khoảng xác định.

- Bước 1 : Tìm TXĐ: D

- Bước 2 : Tính $y\text{'}$. Tìm những điểm mà $y\text{'}=0$ và $y\text{'}$ không xác định

- Bước 3 : Lập bảng biến thiên

- Bước 4 : Dựa vào bảng biến thiên và kết luận GTLN; GTNN

*Lưu ý: GTLN, GTNN của hàm số phải là số hữu hạn

+ Trong một vài TH (thường là hàm phân thức) GTLN, GTNN hữu hạn nhưng đạt tại $x=\pm \infty$. Khi đó ta cũng kết luận là hàm số không có GTLN (GTNN).

3. Cách tính GTLN và GTNN trên một đoạn

a. Định lí

Mọi hàm số liên tục trên một đoạn đều có GTLN và GTNN trên đoạn đó.

b. Quy tắc tìm GTLN, GTNN trên đoạn [a,b]

- Tìm các điểm $x_1,x_2,\mathrm{...}{x}_n$ trên khoảng $\left(a;b\right)$ mà tại đó $f\text{'}\left(x\right)=0$ hoặc $f\text{'}\left(x\right)$ không xác định

- Tính $f\left(a\right),f\left(x_1\right),f\left(x_2\right),\mathrm{...}f\left(x_n\right),f\left(b\right)$.

- Tìm số lớn nhất M và số nhỏ nhất m trong các số trên.

- Kết luận: $\underset{\left[a;b\right]}{\max }f\left(x\right)=M$ và $\underset{\left[a;b\right]}{\min }f\left(x\right)=m$

*Chú ý: Đối với hàm phân thức $y=\frac{ax+b}{cx+d}$. Khi tìm GTLN và GTNN của hàm này trên đoạn $\left[m;n\right]$.

+) Nếu $-\frac{d}{c}\in \left[m;n\right]$ thì hàm số không có GTLN và GTNN

+) Nếu $-\frac{d}{c}\notin \left[m;n\right]$ thì GTLN và GTNN sẽ đạt tại các đầu mút.

4. Các ví dụ

VD1. Tìm GTLN, GTNN của các hàm số sau:

a. $y=x^3+3x^2-9x-7$ trên đoạn $\left[-4;3\right]$

b. $y=x^4-4x^2+3$ trên đoạn $\left[1;3\right]$

Lời giải:

a.

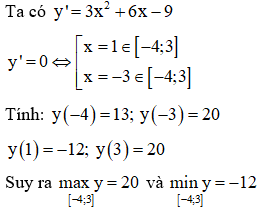
b. 

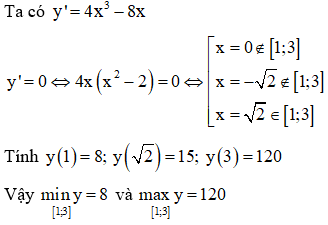
VD2. Tìm GTLN và GTNN của các hàm số sau:

a. $y=x-3+\frac{1}{x}$  trên khoảng $\left(0;+\infty \right)$

b. $y=\frac{x}{4+x^2}$ trên khoảng $\left(-\infty ;+\infty \right)$

Lời giải:

a. Trên khoảng $\left(0;+\infty \right)$, ta có: $y\text{'}=1-\frac{1}{x^2}$;$y\text{'}=0\iff x=1$

Bảng biến thiên

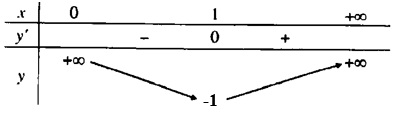
Từ bảng biến thiên ta thấy $\underset{\left(0;+\infty \right)}{\min }y=y\left(1\right)=-1$ và không tồn tại GTNN.

b. $y\text{'}=\frac{4+x^2-2x^2}{{\left(4+x^2\right)}^2}=\frac{4-x^2}{{\left(4+x^2\right)}^2}$.

$y\text{'}=0\iff x=\pm 2$

Bảng biến thiên:

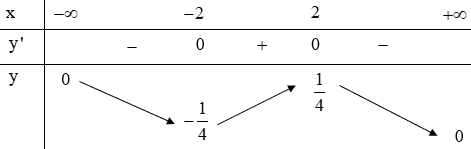
Dựa vào bảng biến thiên ta thấy $\max y=y\left(2\right)=\frac{1}{4}$ và $\min y=y\left(-2\right)=-\frac{1}{4}$

5. Luyện tập

Bài 1. Tìm GTLN và GTNN của hàm số:

a. $y=2x^3-3x^2-12x+8$ trên đoạn $\left[-3;3\right]$

b. $y=\frac{x-1}{x-2}$ trên đoạn $\left[-4;4\right]$

c. $y=x^4-2x^2+3$ trên đoạn $\left[-2;0\right]$

Bài 2. Tìm GTLN, GTNN các hàm số sau:

a. $y=\frac{x^2-3x+3}{x-1}$

b. $\frac{1}{1+x^4}$

Bài 3. Tìm GTLN, GTNN của các hàm số sau:

a. $y=\frac{1}{\sin x}$ trên đoạn $\left[\frac{\pi }{3};\frac{5\pi }{6}\right]$

b. $y=x^3-3x^2-9x+35$ trên các đoạn $\left[-4;4\right]$ và $\left[-5;3\right]$

Bài 4. Tìm hai số có hiệu là 13 sao cho tích của chúng bé nhất.

Bài 5. Một chất điểm chuyển động theo phương trình $x=6t^2-t^3$. Tính thời điểm t (giây) mà tại đó chất điểm có vận tốc lớn nhất.